
Linguisterie |
Linguistique |
Logique PIANOEUDS, out |
Mathématiques,et langage, out |
||
Langage, Biographies |
Psychanalyse |
Topologues/Nodologues, Biographies, |
Mathématiciens Biographies, |
||
Vocabulaire logic, Voc JYG, |
Vocabulaire Math Gén |
||||
Bibliographies, out |
|||||

gaogoa, Mathématiques, |
||||||||||||||||||||||||||||||||||||||||||||||
| Noeud et mathématique, JMV, in TT, 1975, (2), | liens vérifiés, ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
Les liens non encore "traités" peuvent être retrouvés dans la liste alphabétique PIANOEUDS |
- moebius et plan pojectif, cercle, - Moebius et cross-cap, |
|||||||||||||||||||||||||||||||||||||||||||||
| Séminaires de Lacan & Mathématiques, coupures, | Cette page de Définitions, peut être utilement complémentée par celle de PIANOEUDS |
|||||||||||||||||||||||||||||||||||||||||||||
| Séminaires de Lacan, | ||||||||||||||||||||||||||||||||||||||||||||||
| ELP-Lacan-Bibliothèque, | ||||||||||||||||||||||||||||||||||||||||||||||
| MATHEMES de LACAN, J.SIBONI, 2021, & Figures, | Les principaux obstacles à ce travail tiennent à : L'idéologie de l'hégémonie alphabétique et numérique, au bouchon de la Logique classique, érigés en discours Maître, et fossilisée dans les techno-sciences informatiques...et leurs Applications...exponentielles. |
Chronomath, Mathcurve, ScolabLexique, Math93, FERREO, U-Bordeau, |
||||||||||||||||||||||||||||||||||||||||||||
| Symboles logique du séminaire Lacan, et dans les Ecrits, | Utilisez les touches de votre clavier : Ctrl (+) F, pour faire une recherche dans une page, dans un texte, |
|||||||||||||||||||||||||||||||||||||||||||||
| symboles & html, | ||||||||||||||||||||||||||||||||||||||||||||||
| Polices 1 telechrgt | LOGIQUE, gaogoa |
|||||||||||||||||||||||||||||||||||||||||||||
| Symboles Logique, W, | Vocabulaire de mathématiques générales, et de Logiques ...en cours, 2021, 2022, |
|||||||||||||||||||||||||||||||||||||||||||||
| Symboles Math, W, | plus quelques rares termes éclairants du champ psychanalytique, |
|||||||||||||||||||||||||||||||||||||||||||||
| Gras de Tab noir, W, | ||||||||||||||||||||||||||||||||||||||||||||||
« Les mathématiques ne possèdent pas seulement la vérité, mais la beauté suprême, " Les mathématiques sont la seule science où on ne sait pas de quoi on parle, ni si ce qu'on dit est vrai." |
||||||||||||||||||||||||||||||||||||||||||||||
| Mathématiques | ✔ |
Les mathématiques se distinguent des autres sciences par un rapport particulier au réel car l'observation et l'expérience ne s'y portent pas sur des objets physiques ; les mathématiques ne sont pas une science empirique. Elles sont de nature entièrement intellectuelle, fondées sur des axiomes déclarés vrais ou sur des postulats provisoirement admis. Ces axiomes en constituent les fondements et ne dépendent donc d'aucune autre proposition. Un énoncé mathématique – dénommé généralement, après être validé, théorème, proposition, lemme, fait, scholie ou corollaire – est considéré comme valide lorsque le discours formel qui établit sa vérité respecte une certaine structure rationnelle appelée démonstration, ou raisonnement logicodéductif. Un énoncé qui n'a pas encore fait l'objet d'une démonstration mais qui est néanmoins considéré plausible est appelé conjecture. |
Mathématiques, W, |
|||||||||||||||||||||||||||||||||||||||||||
| Logique mathématique | ✔ |
La logique mathématique ou métamathématique est une discipline des mathématiques introduite à la fin du XIXe siècle, qui s'est donné comme objet l'étude des mathématiques en tant que langage. Les objets fondamentaux de la logique mathématique sont les formules représentant les énoncés mathématiques, les dérivations ou démonstrations formelles représentant les raisonnements mathématiques et les sémantiques ou modèles ou interprétations dans des structures qui donnent un « sens » mathématique générique aux formules (et parfois même aux démonstrations) comme certains invariants : par exemple l'interprétation des formules du calcul des prédicats permet de leur affecter une valeur de vérité. |
||||||||||||||||||||||||||||||||||||||||||||
| Logique Canonique Classique | ✔ |
- La logique canonique classique est la première formalisation du langage et du raisonnement mathématique développée à partir de la fin du XIXe siècle en logique mathématique. Appelée simplement logique à ses débuts, c'est l'apparition d'autres systèmes logiques formels, notamment de la logique intuitionniste, qui a suscité l'adjonction de l'adjectif classique au terme logique. A cette époque, le terme de logique classique fait référence à la logique aristotélicienne. La logique canonique classique est caractérisée par des postulats qui la fondent et la différencient de la logique intuitionniste, exprimés dans le formalisme du calcul des propositions ou du calcul des prédicats : La Logique canonique classique, est l'agencement de la théorie de la vérifonctionnalité et de la théorie de la kantification, désormais (LCC). - La logique classique classifie, Et c’est ça le concept, la logique du concept, JMV20110125, |
Logique Canonique classique, |
|||||||||||||||||||||||||||||||||||||||||||
Logique classique, Logique traditionnelle, |
✔ |
- En philosophie, certains1 nomment logique traditionnelle celle qui a existé en Occident après Aristote et avant l'avènement de la logique mathématique moderne. Elle fut dominante en Europe depuis l'Antiquité jusqu'à la fin du XIXe siècle. La logique d'Aristote est présentée dans six documents connus sous le nom d'Organon. Deux de ces documents, les Premiers Analytiques et De l'interprétation, contiennent l'étude des jugements et de l'inférence formelle et c'est cette partie des œuvres d'Aristote qui est passée à la postérité. L'étude contemporaine sur la logique d'Aristote a été initiée par Jan Łukasiewicz. |
↑ | |||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eléments : Zestedesavoir, Dictionnaire des Mathématiques, T1, T2, EU, | ||||||||||||||||||||||||||||||||||||||||||||||
| Algèbre (813-833, W)- Analyse - Arithmétique- Théorie des Nombres - | ||||||||||||||||||||||||||||||||||||||||||||||
| Géométrie - Géométrie différentielle - Courbes algébriques - | des géométries, sa fonction, W, |
|||||||||||||||||||||||||||||||||||||||||||||
| Topologie | ||||||||||||||||||||||||||||||||||||||||||||||
| Algèbre topologique | ||||||||||||||||||||||||||||||||||||||||||||||
| Géométrie Algébrique - | ||||||||||||||||||||||||||||||||||||||||||||||
| voir les Fondements des mathématiques, Crise, supports : Une histoire des mathématiques, DAHAN-DAMEDICO, PEIFFER |
||||||||||||||||||||||||||||||||||||||||||||||
| BOURBAKI, Elements de mathématique, et sur W, | ||||||||||||||||||||||||||||||||||||||||||||||
| Axiomatisation, Loi de composition, Corps, Anneaux, Théorie des groupes, Linéarisation, | ||||||||||||||||||||||||||||||||||||||||||||||
| Analyse, Logique, | ||||||||||||||||||||||||||||||||||||||||||||||
| Ensemble ordonné, Groupe, Espace topologique, Espace disqué , Espace localement annelé, Application, analyse numérique, Probablilité, Logique mathématique, |
||||||||||||||||||||||||||||||||||||||||||||||
| - La Théorie des ensembles ZFC est une théorie des fondement des mathématiques, si elle peut les décrire, elle n'est pas les Mathématiques. - La théorie des ensembles de Zermelo-Fraenkel, ( ZF), (S0T0), ne connait que les ensembles. Son élégance conceptuelle et son aptitude à élaborer en son sein la quasi totalité des outils de la mathématique actuelle l'impose. - Les mathématiques classiques sont bien réductibles, pas intégralement, à la Théorie des ensembles de Cantor. - La Théorie des ensembles peut être écrite grâce à la Logique, et non l'inverse ! Elle dépend d'une certaine manière de la Logique !, |
||||||||||||||||||||||||||||||||||||||||||||||
| A | ||||||||||||||||||||||||||||||||||||||||||||||
| Abélien, | abélien ou commutatif, (Théorie des groupes), voir aussi Analyse, Théorie des nombres, Théorie des catégories, | W, |
||||||||||||||||||||||||||||||||||||||||||||
| Achèvement | ✔ |
- Réunir un discours sur ses énoncés les plus extrêmes,
|
||||||||||||||||||||||||||||||||||||||||||||
Entéléchie, |
- Concept d'Entéléchie, Achèvement, Concept de philosophie métaphysique qui désigne l'état de ce qui a été réalisé, de ce qui a rempli sa fin. Le terme, qui vient de ἐντελής (« complet, achevé »), est parfois difficile à distinguer de l'acte dans les textes d'Aristote. Elle n'est pas pour autant synonyme de l'acte : Aristote appelle ἐνέργεια / energeia la réalisation graduelle, le processus qui mène de la puissance à l'actualisation ; l’entéléchie est l'actualisation à son plus haut degré d'achèvement (ARISTOTE par L.ROBIN, 4 item, 2,) . L'entéléchie est le résultat de l’ἐνέργεια lorsqu'elle ne renferme plus aucune indétermination issue de la matière. |
W, |
||||||||||||||||||||||||||||||||||||||||||||
Affine Espace affine |
✔ | Un espace affine est un espace qui généralise la notion d'espace Euclidien (lui même généralise la géométrie d'Euclide, soit modélise le plan et l'espace, traite des dimensions supérieures des espaces vectoriels sur les nombres réels, de dimension finie, muni d'un produit scalaire pour mesurer angles et distances) en omettant les notions d'angle et de distances. Dans l'espace affine on parle d'Alignement, de Parrallèlisme, de Rapport de proportionnalité. C'est un espace vectoriel dont on a oublié l'origine. Une Translation est une transformation affine, l'Homothétie (dont le centre est un point quelconque de l'espace) , la Transvection ou Dilatation sont des applications affines |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Repère affine, c'est un repère dans l'espace affine qui associe de façon bi-univoque à tout point de l'espace un ensemble de coordonnées dans le corps sur lequel est défini l'espace vectoriel associé. C'est un couple E =[E,V]; E origine du repère, V espace vectoriel. | ||||||||||||||||||||||||||||||||||||||||||||||
| Application affine : est une application entre 2 espaces affines compatibles avec leurs structures, c'est-à-dire qui envoie les droites , plans, espaces, .. sur des droites, plans, espaces .. tout en préservant la notion de parallélisme. Cette notion généralise celle de fonction affine en analyse. | ↑ | |||||||||||||||||||||||||||||||||||||||||||||
| Affirmation | - la proposition, apophantique, empirique | |||||||||||||||||||||||||||||||||||||||||||||
Algèbre(s) \al.ʒɛbʁ\ féminin |
✔ |
- (Mathématiques) Branche des mathématiques qui étudie les structures algébriques, hors des notions de limite (rattachée à l’analyse) et de représentation graphique (concernant la géométrie). - Le mot « algèbre » vient de l'arabe ’al ǧabr (« réduction »), désignant une technique de chirurgie des membres puis une technique de réduction des calculs. Cette dernière donne lieu à plusieurs branches des mathématiques mais aussi, depuis le XXe siècle, à plusieurs structures composées d'un ensemble et de plusieurs opérations. Hors des mathématiques, le terme est parfois employé pour désigner un ensemble de règles, avec une connotation de rigueur ou d'hermétisme. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
L'algèbre regroupe le traitement de formules et d'équations reliant des objets mathématiques par des opérations.
|
↑ | |||||||||||||||||||||||||||||||||||||||||||||
Structures Une structure d'algèbre sur un ensemble est en général constituée de deux lois de composition internes, la première (additive) étant commutative et associative, la seconde (multiplicative) étant distributive par rapport à la première. Elle peut être munie de structures additionnelles ou assortie de conditions supplémentaires. |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
Algèbre sur un anneau ou un corps Une algèbre sur un anneau est un module sur cet anneau muni d'une loi multiplicative compatible. Une algèbre sur un corps est un espace vectoriel muni d'une loi multiplicative compatible. PropriétésUne telle algèbre est dite :
|
↑ | |||||||||||||||||||||||||||||||||||||||||||||
| ALGEBRE | ✔ |
Etude des structures algébriques, | source principale : E.U, |
|||||||||||||||||||||||||||||||||||||||||||
Depuis 813, au Traité de base d'algèbre d'Al-KHWÂRIZMÎ, (780-850) Précis sur le calcul de al-jabr (complément ou remplissage), qui décrit la résolution d'équations type (ax2 = bx), nécessités alors par le difficile partage des héritages dans le droit musulman, s'y substitue de nouvelles idées. De nouveaux Êtres mathématiques doivent aider à surmonter les impasses des calculs anciens, en théorie des nombres et des équations complexes... Les objets étudiés deviennent secondaire pour révéler les analogies, les points communs. |
1) ax2 = bx, 2) ax2 = c, 3) bx = c, 4) ax2+ bx = c 5) ax2 = bx, 6) bx + c = ax2 |
|||||||||||||||||||||||||||||||||||||||||||||
| Axiomatisation de l'algèbre, | Axiomatisation |
|||||||||||||||||||||||||||||||||||||||||||||
| 1850 - Les anglais dégagent la notion de Loi de composition qu'ils appliquent aux vecteurs, matrices, à l'algèbre de la logique. | Loi de composition, W, |
|||||||||||||||||||||||||||||||||||||||||||||
| 1910 - Synthèse de Ernst.STEINITZ, (1871-1928) dans Théorie algébrique des corps, 1910, où il étudie la théorie axiomatique des corps commutatifs et définit des concepts comme corps premier, corps parfait et degré de transcendance d'une extension de corps. Il démontre que tout corps possède une cloture algébrique. Il réalise également un important travail sur les graphes ....les polyèdres, Son travail marque le début de l'Algèbre moderne. |
Théorie axiomatique des corps commutatifs, Corps premier, Corps parfait, Degré de transcendance d'une extension de corps, Cloture algèbrique, Théorie des graphes, |
|||||||||||||||||||||||||||||||||||||||||||||
| CAUCHY (1789-1857) et GALOIS abordent l'étude des Groupes (structure algèbrique) qui se révelera de première importance pour la théories des équations, en physique, et en théorie quantique. | ||||||||||||||||||||||||||||||||||||||||||||||
| Corps, Anneaux commutatifs émergent des études allemandes sur les nombres algébriques. Ils permettent l'étude des courbes, des surfaces algébriques, puis la géométrie algébrique, permettant l'introduction d'un langage géométrique en algèbre commutatif. |
Corps, Anneaux commutatifs Géométrie algébrique, |
|||||||||||||||||||||||||||||||||||||||||||||
| Linéarisation : l'Algèbre linéaire se développe avec la compréhension du caractère linéaire de nombreuses situations et donc du processus de linéarisation. | Linéarisation, W, |
|||||||||||||||||||||||||||||||||||||||||||||
L'Algèbre |
✔ |
rejoint l'Analyse par la considération sur un même ensemble de structure algèbrique et de structures topologiques (source de l'algèbre topologique) L'analyse 1 [ (du grec άναλύειν, analuein),], selon W, 2 [(« analusis » qui signifie « décomposition », lui-même formé à partir d'un verbe simple "luein" qui signifie "décomposer")], source lettresorléans, 3 [ analysis, de ἁναλύω, analuô (« délier »), de ἀνά, ana (« en haut »), et λύω, luô (« relâcher ») ], source wiktionary, 4 [ Empr. au gr. α ̓ ν α ́ λ υ σ ι ς, attesté dep. Aristote au sens de « dissolution » (Du monde, 4, 11 ds Bailly), et de « analyse, méthode de résolution (p. opp. à la synth.) » (Morale à Nicomaque, 3, 3, 12 ds Bailly)], selon cnrtl, a pour point de départ la formulation rigoureuse du calcul infinitésimal. C'est la branche des mathématiques qui traite explicitement de la notion de limite, que ce soit la limite d'une suite ou la limite d'une fonction. Elle inclut également des notions comme la continuité, la dérivation et l'intégration. Ces notions sont étudiées dans le contexte des nombres réels ou des nombres complexes. Cependant, elles peuvent aussi être définies et étudiées dans le contexte plus général des espaces métriques ou topologiques. |
L'Analyse, W, Limite(s), Continuié, Dérivation, Intégration, |
|||||||||||||||||||||||||||||||||||||||||||
Algèbre |
✔ |
- (de al jabr = réduction) - L'algèbre élémentaire est consacrée à l'étude des nombres et des relations entre nombres grâce à des manipulations sur les lettres qui les remplacent. L'algèbre dite moderne étudie des structures crées par les opérations dans les ensembles de nombres. Dedelicq. - d’un point de vue algébrique aux structure algébriques de groupe on fait correspondre des structures linéaires qui s’appellent modules, aux corps on fait correspondre les espaces vectoriels, c’est ce qu’on étudie en géométrie, et c’est là qu’on développe le calcul matriciel, et puis aux anneaux, il y a une structure linéaire qui correspond aux anneaux, entre les modules et les espaces vectoriels il y a les algèbres, donc vous avez Groupe, anneaux, corps, et vous avez module, algèbre et espace vectoriel, JMV09062015 |
||||||||||||||||||||||||||||||||||||||||||||
Algèbre |
✔ |
- L'algèbre est une branche des mathématiques qui permet d'exprimer les propriétés des opérations et le traitement des équations et aboutit à l'étude des structures algébriques. Selon l’époque et le niveau d’études considérés, elle peut être décrite comme :
Le domaine d'application de l'algèbre s'étend des problèmes arithmétiques, qui traitent de nombres, à ceux d'origine géométrique tels que la géométrie analytique de Descartes ou les nombres complexes. |
||||||||||||||||||||||||||||||||||||||||||||
Logique & Algèbre, |
- La logique s'accompagne d'une algèbre constuite sur un espace vectoriel ou un anneau | |||||||||||||||||||||||||||||||||||||||||||||
| Algèbre de Boole | ✔ |
- voir Boole ci-dessous Pour tout ensemble, l'ensemble de ses parties est une algèbre de Boole, l'ordre associé étant l'inclusion et les lois d'anneau la différence symétrique et l' intersection . Un autre exemple est donné par l'ensemble des formules du calcul propositionnel prises à équivalence (en logique classique) près (sur un nombre de variables de cardinal arbitraire), l'ordre associé est la relation de conséquence logique, les lois d'anneau la disjonction exclusive et la conjonction . (source Wiki ) |
||||||||||||||||||||||||||||||||||||||||||||
| Algèbre de Boole ou Théorie de la coordination |
✔ |
- L'Algèbre de Boole, Boole voulait construire un calcul pour la quantification ( et des concepts) S1T1et la syllogistique d'Aristote, MAIS aujourd'hui, au XX et XXI siècle, elle passe pour une bonne écriture du calcul de la coordination ...S2T2 - Z2 - L'algèbre de Boole, aujourd'hui, c'est la bonne écriture pour la Théorie de la coordination |
||||||||||||||||||||||||||||||||||||||||||||
| Algèbre de Lacan |
✔ |
- a, - fonts Lcan(zip) |
||||||||||||||||||||||||||||||||||||||||||||
| - c'est une algèbre de Boole... Présentation : Table des matières, Cours : JMV22062010, L177, | ||||||||||||||||||||||||||||||||||||||||||||||
Algèbre générale (/algèbre élémentaire) |
✔ |
- L'algèbre générale, ou algèbre abstraite, est la branche des mathématiques qui porte principalement sur l'étude des structures algébriques et de leurs relations. L'appellation algèbre générale s'oppose à celle d'algèbre élémentaire ; cette dernière enseigne le calcul algébrique, c'est-à-dire les règles de manipulation des formules et des expressions algébriques.
Historiquement, les structures algébriques sont apparues dans différents domaines des mathématiques, et n'y ont pas été étudiées séparément. C'est pourquoi l'algèbre générale possède beaucoup de connexions avec toutes les branches des mathématiques. L'étude des structures algébriques peut être faite de manière abstraite, mais unifiée dans le cadre de l'algèbre universelle. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Structures algébrique, |
✔ |
En mathématiques, plus précisément en algèbre générale et en algèbre universelle, une structure algébrique est un type particulier de structure. Sa spécificité par rapport aux autres types de structure est d'être formée d’un ensemble combiné à une ou plusieurs lois de composition, éventuellement complétées par un ordre ou une topologie, le tout satisfaisant un certain nombre d'axiomes. En algèbre générale, les structures algébriques sont définies une à une et leurs propriétés sont étudiées séparément. En algèbre universelle, les structures algébriques sont étudiées de façon globale de façon à obtenir un modèle unifié, d'où l'adjectif « universel ». Par exemple, qu'y a-t-il en commun entre la théorie des groupes, la théorie des anneaux et la théorie des corps? L'objectif de cet article est de dresser une liste des structures algébriques usuelles et de les classer. |
||||||||||||||||||||||||||||||||||||||||||||
| Algèbres de von Neumann | – algèbres des opérateurs bornés qui agissent sur un espace de Hilbert –, domaine où le mathématicien français Alain Connes venait d’obtenir d’importants résultats. | EU |
||||||||||||||||||||||||||||||||||||||||||||
| Aliénation, | ✔ |
- ou, implication non réciproque - les 3 formes du OU, 1, 2, |
||||||||||||||||||||||||||||||||||||||||||||
| - Voir Vel, -- Vel de l'aliénation,<≠, il est l'abréviation de l'expression formée par les seuls connecteurs primitifs de la négation et de la disjonction exclusive classique. - Kant avec Sade, Lacan, Ecrits - Clef pour la passe, 1ere partie, argument 3, dans L'amour du tout, JMV - Le vel de l'aliénation, 2006, JMV , construction en logique classique |
||||||||||||||||||||||||||||||||||||||||||||||
| Analyse, | ✔ |
L'analyse a pour point de départ la formulation rigoureuse du calcul infinitésimal. C'est la branche des mathématiques qui traite explicitement de la notion de limite, que ce soit la limite d'une suite ou la limite d'une fonction. Elle inclut également des notions comme la continuité, la dérivation et l'intégration. Ces notions sont étudiées dans le contexte des nombres réels ou des nombres complexes. Cependant, elles peuvent aussi être définies et étudiées dans le contexte plus général des espaces métriques ou topologiques. Les fondements de l'analyse ne sont pas abordable sans présenter au préalable des éléments d'algèbre, de topologie, de théorie des fonctions, ... |
Limites, continuité, dérivation, intégration, pour les domaines des nombres Réels, des nombres Complexes, des espaces métriques ou topologiques, |
|||||||||||||||||||||||||||||||||||||||||||
Eléments de mathématique. & développement BOURBAKI, |
✔ |
ÉLÉMENTS DE MATHÉMATIQUE PREMIERE PARTIE • I. Théorie des ensembles • II. Algèbre • III. Topologie générale • IV. Fonctions d'une variable réelle • V. Espaces vectoriels topologiques • VI. Intégration DEUXIÈME PARTIE • Groupes et algèbres de Lie • Algèbre commutative • Théories spectrales • Variétés différentielles et analytiques Éléments d'histoire des mathématiques Articles |
||||||||||||||||||||||||||||||||||||||||||||
| Analyse | ✔ |
- Analyse, sur Cnrtl, : décomposition d'une chose en ses éléments... - que n’importe quelle analyse, c’est un traitement de la psychose, c’est pas seulement le traitement possible, c’est-à-dire celui qui pourrait ne pas avoir lieu, c’est le traitement contingent de la psychose, le traitement contingent de la psychose c’est la psychanalyse, c’est en analysant névrose et perversion, que le sujet est invité à reconquérir la lecture, et à construire justement un objet qui n’est pas un Savoir, qui n’est pas une Vérité, qui est comme l’objet transitionnel, il est pris dans l’éclatement de l’objet répulsif de la phobie et attractif de la perversion, dans l’éclatement du désir dans le corps, à partir du moment de l’incorporation, vous avez des enfants qui fabriquent cet objet, qui n’est pas une synthèse, mais qui est un objet bien construit, c’est un objet transitionnel, ça veut dire quoi, c’est un objet répulsif, répugnant même, et attractif en même temps, et faire rentrer ça à l’âge adulte, dans son existence, construire ce type d’objet, je vous dis c’est comme une boussole, ça vous permet d’apprendre à lire, donc une psychanalyse, c’est une pratique de cette tâche analysante qui consiste ensuite à être mordu par ça, et ensuite à faire ça toute sa vie, JMV20150602, - Analyse finie, analyse infinie, JMV20150602, - Mathématique, (wiki), - L'analyse en mathématique traite de toutes les notions relatives aux nombres Réels, (Nombres) - Psychanalyse, |
||||||||||||||||||||||||||||||||||||||||||||
| Analyse combinatoire | ✔ |
- ou Combinatoire, voir combinatoire - voir Permutation |
||||||||||||||||||||||||||||||||||||||||||||
| Analyse situs | ✔ |
- Déterminer ce qui concerne la situation par une analyse des propriétés internes de la figure, constitue l'analysis situs. Son originalité réside dans l'abandon des préocupations métriques (mesure), paradoxe si l'on s'en tient à la définition de la géométrie comme manière de mesurer toute chose ! Essaim p 24 | ||||||||||||||||||||||||||||||||||||||||||||
| Anneau | ✔ |
-Groupe, anneaux, corps et module, algèbre, espace vectoriel ! et on les connait bien ceux là, les espaces vectoriels, parce que ça sert en géométrie, avec les vecteurs, c’est pour ça que ça s’appelle espace vectoriel, on a appris ça en mécanique, celle de Newton, la mécanique se fait dans un espace vectoriel, JMV27012015, |
||||||||||||||||||||||||||||||||||||||||||||
Pourquoi des ensembles, des groupes, des anneaux, des corps ?« Ensemble », « groupe » et « corps » ont le sens de « regroupement d’individus », avec une cohésion croissante (pour « corps », penser à « corps de métier, corps diplomatique »).Seul anneau semble faire exception, mais ce mot est traduit de l’allemand Ring qui signifie aussi dans cette langue « cercle » (comme dans « cercle philatélique »). Notons que si les ensembles s’appellent généralement E, les groupes G, et les anneaux A, les corps sont désignés par K, car corps se dit en allemand Körper. Dans un texte anglais, ils seront désigné par F, car corps se dit field (= « champ »). Le mot « ensemble » est probablement dû à l’Allemand Georg Cantor en 1883 (sous sa forme allemande de Menge qui signifie aussi « foule »), le mot « groupe » au Français Évariste Galois en 1830, les mots « anneau » et « corps » (sous la forme Ring et Körper) à l’Allemand Richard Dedekind en 1871 dans son livre : Lehrbuch des Algebra. |
||||||||||||||||||||||||||||||||||||||||||||||
| - En algèbre, on appelle anneaux certains ensembles munis d'une addition et d'une multiplication.
Deux définitions différentes sont significativement représentées dans la littérature mathématique :
|
anneau, W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
Anneau commutatif, |
- Un anneau commutatif est un anneau dans lequel la loi de multiplication est commutative. ( En mathématiques, et plus précisément en algèbre générale, une loi de composition interne L’étude des anneaux commutatifs s’appelle l’algèbre commutative. Les exemples les plus simples de lois commutatives sont sans doute l'addition et la multiplication des entiers naturels. L'addition et la multiplication des nombres réels et des nombres complexes, l'addition des vecteurs, l'intersection et la réunion des ensembles sont également des lois commutatives. À l'inverse, la soustraction, la division, la multiplication des matrices, la composition d'applications et la multiplication des quaternions sont des lois non commutatives. |
|||||||||||||||||||||||||||||||||||||||||||||
| Apodictique, notion scientiste pour JYG |
✔ |
- Est apodictique, du grec ancien ἀποδεικτικός (qui démontre, qui prouve), ce qui présente un caractère d'universalité et de nécessité absolue. Une proposition apodictique est nécessairement vraie, où que l'on soit. Dans le cadre de la logique aristotélicienne, la forme apodictique est opposée à la dialectique, à l'instar de la preuve scientifique s'opposant à un raisonnement de nature probabiliste. Le mot anapodictique (qui signifie « indémontrable » chez Aristote) représente les prémisses premières et immédiates d'où part le syllogisme apodictique : ses axiomes. On peut par exemple penser aux principes classiques de la logique formelle : le principe d'identité, le principe de non-contradiction, le principe de bivalence et celui de tiers exclu. Kant oppose le jugement apodictique, qui est démontré ou immédiatement nécessaire, au jugement assertorique, dont la vérité n'est pas démontrée ni immédiatement nécessaire, et au jugement problématique qui ne présente qu'un caractère de vraisemblance ou de possibilité - Gödel, 1931, incomplétude, Hilbert, ..c'est la force de la Logique classique |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Apophantique | ✔ |
- relatif à la parole, - affirmation, la proposition, empirique, - apophantique chez Aristote ça veut dire les énoncés constatifs, suite .. |
||||||||||||||||||||||||||||||||||||||||||||
| Arbre, | Un arbre est un graphe connexe, sans cycle. Les sommets extrémaux sont appelés ses feuilles. Ce sont des sommets de degré 1. Si un arbre contient au moins trois sommets, alors chaque feuille est contenue dans une unique arête, qu'on appelle brindille, Les arbres jouissent d’une propriété héréditaire très utile, qui est l’affirmation suivante. Propriété héréditaire. Si, dans un arbre, on supprime une feuille et sa brindille, alors le graphe résultant est encore un arbre. suite ici --> |
images-math.cnrs, | ||||||||||||||||||||||||||||||||||||||||||||
| Arité | ✔ |
- nombre d'arguments que requiert une fonction, une opération - L'arité peut être unaire, binaire, ternaire, ....; la fonction inverse, qui associe à un nombre son inverse, est unaire; l'addition de deux nombres est une opération ou fonction binaire. - on parle en logique de l'arité du prédicat ou d'une relation : = est une relation binaire tout comme ∈ et <. |
||||||||||||||||||||||||||||||||||||||||||||
| Arithmétique | ✔ |
- Branche des mathématiques, qui se limitait autrefois à l'étude des propriétés des entiers naturels, des entiers reltatifs, des nombres rationnels (sous forme de fractions) et aux propriétés concernant ces nombres. Aujourd'hui, elle comprend une partie de la théorie des nombres qui utilise des méthodes de la géométrie algébrique et de la théorie des groupes. C'est la science des Nombres. (Source wiki) |
- Entiers, relatifs, rationnels, N, Z, Q, R.., 2, - Nombres, sentier des ... - Géométrie algébrique, W, - Théorie des groupes, W, W, |
|||||||||||||||||||||||||||||||||||||||||||
| Axiome, | ✔ |
Axiomes ou Règles de bases, à partir desquels sont déduits par raisonnements logiques des théorèmes. Le but est de fournir une charpente hiérachisée par des structures abstraites aux mathématiques. |
||||||||||||||||||||||||||||||||||||||||||||
| - ce qui est digne, convenable, évident en soi, de axios = digne Vérité indémontrable, qui doit être admise. L'ensemble des axiomes forment une axiomatique. L'axiome est à la logique mathématique ce qu'est le psostulat à la physique théorique. - propositions que la théorie considère vraie sans démonstration. Ce sont les fondements des mathématiques.(L.PUJO-MENJOUET_Fonfamentaux,) - énoncé premier considéré comme vrai dans une théorie mathématique. Les théorèmes sont les énoncés déduits du système d'axiomes considéré. Deledicq.A. - propositions que l'on admet sans démonstration et qui ne sont pas des définitions. Ces propositions ou axiomes, ou postulats (terme obsolète) , sont le point de départ de la théorie que l'on se propose d'édifier. EU81 - Axiome de Boole, 00 = 0 ; 11 = 1 ; et ça c’est ce qu’on appelle l’axiome de Boole, JMV27012015; x² = x, (JMV26062015 ?), (JMV20150602),(.html), |
||||||||||||||||||||||||||||||||||||||||||||||
| Axiomatique | ✔ |
- Méthode axiomatique est un mode d'exposition des sciences exactes fondé sur les propositions admises sans démonstration et nettement formulées et des raisonnements rigoureux. - L'axiomatique commence par l'inventaire exhaustif de toutes les propositions que l'on admet sans démonstration et qui ne sont pas des définitions. Ces propositions ou axiomes, ou postulats, sont le point de départ de la théorie que l'on se propose d'édifier. EU81 |
||||||||||||||||||||||||||||||||||||||||||||
| Axiomatisation, | ✔ |
- En mathématiques, l'axiomatisation d'une théorie est un procédé qui consiste à organiser celle-ci en la fondant sur des axiomes, et à en déduire rigoureusement des théorèmes, dans un cadre qui peut être purement logique, ou celui de la théorie des ensembles. L'ensemble constitue une théorie axiomatique. .... -L'axiomatisation de la géométrie par Euclide dans ses Éléments est le premier exemple historique d'une telle démarche. La démarche axiomatique a été remise à l'honneur par Moritz Pasch et s'est généralisée en mathématiques à la fin du XIXe siècle avec la découverte de nouvelles géométries, le développement de l'algèbre, l'axiomatisation de la géométrie réelle par David Hilbert, l'arithmétisation de l'analyse avec la construction des nombres réels, le développement de la théorie des ensembles, axiomatisée au début du XXe siècle par Zermelo puis Fraenkel et Thoralf Skolem, qui donne un cadre axiomatique général aux mathématiques, et plus généralement les recherches entreprises sur les fondements des mathématiques. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| B | ||||||||||||||||||||||||||||||||||||||||||||||
| Bande de Moebius | ✔ |
- voir Moebius - Bande de Moebius dans le tore, JMV16062015, L240 - Passage du tore à la bande de Moebius, dans Etoffe, JMV |
||||||||||||||||||||||||||||||||||||||||||||
| Bijection | ✔ |
- Application d'un ensemble dans une autre telle que tout élément de l'ensemble d'arrivée, est l'image d'un unique élément de l'ensemble de départ. | ||||||||||||||||||||||||||||||||||||||||||||
| Bilatère | ✔ |
- signifie que la surface a deux faces (comme un disque), elle est orientable . (Noeud) p61 - s'il existe dans un Nœud un vide de valence impaire, alors la surface du nœud est unilatère. Np66 |
||||||||||||||||||||||||||||||||||||||||||||
| Boole | ✔ |
- Boole sur wiki |
||||||||||||||||||||||||||||||||||||||||||||
✔ |
- Logique de Boole, Algèbre de Boole, - Boole veut faire une nouvelle arithmétique, et écrire la syllogistique d'Aristote et la faire rentrer dans le calcul des Prédicats quantifiés S1 T1 - Boole permet de ne plus faire d'initiations ( l'initiation est le fait de faite entrer les idéaux d'une société dans le corps, par les orifices). Les mathématiques sont enseignables grâce à Cantor. - JMV02022011, l'initiation Lacan réduit la psychanalyse à la Théorie des ensembles, JMV16062015, - Voir George Peacock. |
|||||||||||||||||||||||||||||||||||||||||||||
Algèbre de Boole |
✔ |
- une algèbre de Boole c’est fait avec, c’est une arithmétique sur les nombres entiers modulo 2, ce qui fait dire à certain que la logique est binaire. cours de JMV20150127, On va voir qu’elle n’est pas binaire, puisqu’elle peut être quaternaire, avec huit éléments ou seize éléments, ou toute puissance de deux, donc c’est pas binaire, mais c’est de caractéristique deux. 00 = 0 ; 11 = 1 ; et ça c’est ce qu’on appelle l’axiome de Boole - Algèbre de Boole, logique de Boole, ou calcul booléen, partie des mathématiques ou de la logique ou de l'électronique qui s'intéresse aux opérations et fonctions sur les variables logiques. L'algèbre booléen permet d'ulitiser des techniques algébriques pour traiter les expressions à deux valeurs du calcul des propositions. ( V, F), ( 0, 1), ( +, - ), (B, ¬ B), - l'algèbre de Boole n'est pas un code, et n'est pas réductible à son modèle électrique qui ravage la planète ( et supporte le présent texte), les valeurs 0 et 1 expriment ( dans la représentation E-V, soit la zone (dedans dehors) pour la coordination et les concepts, soit la valeur (Faux Vrai)), pour la Th des E... à suivre - Les calculs de Boole vont être dans la logique formelle constituée du système de la coordination et du calcul des prédicats du premier ordre kantifiés, ils vont être des calculs algébriques entre ces deux calculs, on peut écrire dans le calcul de Boole le calcul de la coordination et on peut écrire les quantifications entre les prédicats, Boole alors considère seulement un seul type,et il voit qu'il y a deux versions de algèbre en matière de coordination, c'est ainsi présenté par Couturat, - entre proposition et concept, et ils vont découvrir la nécessité du métalangage, révélée par Jakobson, dans la Linguisitique, mais qui déjà se trouve chez Frege sous le nom de langue auxiliaire, à côté des langues formulaires JMV22062010, nécessité d'une langue auxiliaire pour le commentaire, c'est la formule de Frege, le mot de métalangage ne viendra que plus tard, et chez Boole ça s'appelle la différence entre les énoncés primaires et les énoncés secondaires, il y a des énoncés qui traitent des énoncés primaires, et alors il faut réduire les primaires au calcul des propositions, d'où ce nom, mais le même calcul se produit pour les concepts et les deux sont mélangés. - entre proposition et concept, et ils vont découvrir la nécessité du métalangage, révélée par Jakobson, dans la Linguisitique, mais qui déjà se trouve chez Frege sous le nom de langue auxiliaire, à côté des langues formulaires JMV22062010, nécessité d'une langue auxiliaire pour le commentaire, c'est la formule de Frege, le mot de métalangage ne viendra que plus tard, et chez Boole ça s'appelle la différence entre les énoncés primaires et les énoncés secondaires, il y a des énoncés qui traitent des énoncés primaires, et alors il faut réduire les primaires au calcul des proposition, d'où ce nom, mais le même calcul se produit pour les concepts et les deux sont mélangés. Vous avez des fonctions propositionnelle qui sont des concepts, sur lesquel on applique le calcul de la coordination....; L150, ..., nous allons utiliser ces écritures pour la psychanalyse et entrer dans une algèbre de Lacan qui va être une algèbre de Boole, - la négation logique, - , l'algèbre de Boole , c'est une arithmétique curieuse, vous avez + 1 = - 1, alors on se dit il n'y a plus de différence entre le positif et le négatif, la différence importante dans l'algèbre de Boole, c'est le zéro, 0, soit l'élément neutre de l'addition, et le un, 1, l'élément neutre de la multiplication, donc l'algèbre de Boole est construite sur une différence entre addition et multiplication, pas entre 0 et 1, en tant que valeur, mais éléments neutres de deux opérations différentes, il faut y réfléchir à propos du zéro et du un, et puis ça se démultiplie l'algèbre de Boole, 1.00.45, cour de JMV23092014 (2) voir cours 2014, - algèbre de Boole et corps de Galois, JMV20150602, p9 - Voir Algèbre de Boole, ( cette section autour de l'Algèbre de Boole, sous forme de cut-up, doit être réorganisée pour clarification) |
||||||||||||||||||||||||||||||||||||||||||||
| JMV20110301,(dispo en 06_2023), l’Algèbre de Boole c’est un métalangage du langage de la coordination, | ||||||||||||||||||||||||||||||||||||||||||||||
| Bord | ✔ |
- le bord d'une surface topologique est la réunion des segments des morceaux d'étoffe qui n'on par servi au montage par couture. Le bord de la surface (une cercle) est un composé, une réunion de cercles distincts ou composants de bord, et ces composants du bord forment le Nombre de bord. Un trou comme rupture de surface est défini par un cercle composant du bord d'une surface topologique. Le trou imaginable intuitif peut alors être réduit à un invariant bien construit, le composant de bord. Il n'y a pas de trou imaginable dans la suface intrinsèque, seul son bord y insiste, et le trou existe pour nous. Ceci pour un type de trou parmi les trous ….Etoffe P79 A toute surface topologique avec ou sans bord correspond une surface sans bord. |
||||||||||||||||||||||||||||||||||||||||||||
Borroméen ou Chaine Bruniennes |
✔ |
- 3333-3333, et transformations du Bo aux 2Ch aux Noeuds propres, ou .pdf, - Chaine borroméenne de 3 noeuds de Trèfle, JMV leçon du 04 septembre 2007 |
||||||||||||||||||||||||||||||||||||||||||||
| Borroméen Généralisé | ✔ |
-- 4444-6552, .pdf, .swf, - Bog, suite des définitions - Avec sa couleur de femme vaporeuse, vient sur le tard, au moment ou Lacan s'interroge sur Litilth, le troisième sexe . Pourquoi deux ne suffisent pas, le troisième ne tiendrait pas en présence des deux autres. Ce qui tient dans le noeud, est définit par les institutions du sujet, (identifications et structure de la foule), où commence le symptôme. Pour ce noeud c'est une fonction de manque absolu . - du noeud borroméen généralisé : "lorsque Lacan l’annonce au début de l’année,(S XXVI intitulé La topologie et le temps (leçon du 21 novembre 1978)) de la généralisation des chaînes bruniennes (autre nom du borroméen) esquissée par Debrunner et achevée par Penney qui construisent, chacun de manière de plus en plus élégante, ce type de chaînes"... - "des noeuds borroméens fort généralisés, il s’agit d’un nouveau type d’objets, invisible à une quelconque théorie des noeuds hors la classique. Il est des plus simples à pouvoir se défaire, à la fois, par des mouvements impropres à l’exclusion des autres, comme un noeud borroméen, ou d’une part, par des mouvements hybrides exclusifs, comme une chaîne de Whitehead, mais, ce qui est encore plus surprenant, d’autre part, par des mouvements propres à l’exclusion de tous les autres, comme un noeud propre, un noeud trèfle par exemple, alors qu’il s’agit d’une chaîne et borroméenne de surcroît " -JMV in : " ça claque " - Généralisation du noeud borroméen, Lacan, la Topologie et le temps, SXXVI, 21 novembre 1978, - voir cours JMV11092007, |
||||||||||||||||||||||||||||||||||||||||||||
| Borroméen fort généralisé ↑ | ✔ |
- 4444-8554, .pdf, .swf, - sur ce site parfois nommé, Boforgé, - "des noeuds borroméens fort généralisés, il s'agit d'un nouveau type d'objets, invisible à une quelconque théorie des noeuds hors la classique. Il est des plus simples à pouvoir se défaire, à la fois, par des mouvements impropres à l'exclusion des autres, comme un noeud borroméen, ou d'une part, par des mouvements hybrides exclusifs, comme une chaîne de Whitehead, mais, ce qui est encore plus surprenant, d'autre part, par des mouvements propres à l'exclusion de tous les autres, comme un noeud propre, un noeud trèfle par exemple, alors qu'il s'agit d'une chaîne et borroméenne de surcroît " - JMV souligne l'emabarras que cela pose à la théorie positive des noeuds , dans le sens de l'échec des tentatives de faire correspondre des invariants algèbriques à ces objets topologiques. - le Boforgé ne se trouve que dans la théorie positive des modèles physiques, . Dans les autres théories (voir ci-dessus), il disparait dès la première ligne, par quatre mouvements noeuds (propre, ou hybride, ou impropre). -"ça claque"", JMV, revue Essaim, 2008 - voir noeud borroméen généralisé, |
||||||||||||||||||||||||||||||||||||||||||||
| Borroméen hyper généralisé | ✔ |
- 4444-7654, | ||||||||||||||||||||||||||||||||||||||||||||
| Bouteille de Klein | ✔ |
- la bouteille de Klein est associée à la voix dans l'analyse. - Les surfaces topologiques intrinsèques, - Surface topologique unilatère, |
||||||||||||||||||||||||||||||||||||||||||||
| Brunn | ✔ |
- De Brunn à Debrunner, | ||||||||||||||||||||||||||||||||||||||||||||
| Burali-Forti | ✔ |
En mathématiques, le paradoxe de Burali-Forti, paru en 1897, désigne une construction qui conduit dans certaines théories des ensembles ou théories des types trop naïves à une antinomie, c’est-à-dire que la théorie est contradictoire (on dit aussi incohérente ou inconsistante). Dit brièvement, il énonce que, comme on peut définir la borne supérieure d'un ensemble d'ordinaux, si l'ensemble de tous les ordinaux existe, on peut définir un ordinal supérieur strictement à tous les ordinaux, d'où une contradiction. | W, |
|||||||||||||||||||||||||||||||||||||||||||
| C | ||||||||||||||||||||||||||||||||||||||||||||||
| Calcul booléen | ✔ |
- voir BOOLE, calcul de .., Algèbre de BOOLE, Axiome de Boole, | ||||||||||||||||||||||||||||||||||||||||||||
Calcul de la coordination ou Calcul des propositions, ou L2T2
|
✔ |
- voir coordination - Le calcul de la coordination met l'accent sur les connecteurs logiques (OU, ET), leurs fonctions, plutôt que sur les objets, les lettres, comme dans le calcul des propositions qu'on devrait plutôt nommer calcul des énoncés (Rivenc et Vappereau) car portant sur des propositions ET des concepts ! -JMV22062010 ENS, L56- La logique c'est ce système de la coordination, plus ce que nous allons appeler le calcul des prédicats du premier ordre kantifiés, écrit avec un k, ces deux calculs forment la logique formelle, c'est le noyau de la logique, pour la science, et depuis les calculs de Boole et de Frege s'inscrivent là-dedans. JMV22062010-L130, -la logique au niveau de la coordination, c’est de la grammaire, mais les grammairiens abandonnent ça aux logiciens parce que, il y a une histoire de vérité qui va apparaître, un calcul sur le Vrai et le Faux . - la coordination c’est quoi, c’est l’étude des connecteurs de coordination, vous avez ça dans le Grevisse, dans les Grammaires du français, qu’est ce qu’on peut faire avec des propositions, dans la langue, soit il y a la subordination, la principale et la subordonnée, soit il y a la coordination par des connecteurs, V01-47.00 ; qui sont appelés des conjonctions de coordination, et Grevisse il renvoie la coordination aux logiciens, il dit maintenant si vous voulez étudier la coordination des propositions dans la langue, il faut faire de la logique, par contre la grammaire elle traite de la subordination, JMV20150602, - moi j’insiste sur le fait de la coordination, parce que la coordination c’est la coordination des propositions, dans ce qu’on appelle le Calcul des propositions, mais c’est les coordinations qui nous intéressent, parce que ce calcul de la coordination il est présent deux fois dans le Calcul des prédicats, réfléchissez, parce que là on rentre dans une structure narcissique, dans un nœud, dans quelque chose qui est intrinsèque et extrinsèque, qui est double et qui est un, c’est ça qui est intéressant, c’est dans l’écriture, là on est franchement plus dans l’écriture que dans la parole, on est dans la langue, mais on s’écarte de la langue parlée, on est dans la langue écrite, et on est dans l’écriture, dans le système d’écriture. JMV20150602, - que la notion de fonction propositionnelle, de concept, c’est quelque chose qui est ouvert, c’est un énoncé ouvert, et quand on va la kantifier, ou l’instancier, il va devenir un énoncé clos, fermé, et donc dans la logique des concepts, des prédicats, vous avez à la fois des concepts, des fonctions propositionnelles ET des propositions, puisque on peut transformer un prédicat, un concept en proposition, de cette manière là, donc vous avez deux régimes de la coordination, ... JMV20150602. - Clef pour la passe, 2 eme partie, dans L'amour du tout, JMV, effet sur le calcul de la coodination - lecture des formules kantiques de la sexuation (texte intégral simplifié), 2007, JMV |
||||||||||||||||||||||||||||||||||||||||||||
| Le calcul des propositions ou calcul propositionnel fait partie de la logique mathématique. Il a pour objet l'étude des relations logiques entre « propositions »1 et définit les lois formelles selon lesquelles les propositions complexes sont formées en assemblant des propositions simples au moyen des connecteurs logiques et celles-ci sont enchaînées pour produire des raisonnements valides. Il est un des systèmes formels, piliers de la logique mathématique dont il aide à la formulation des concepts 2. Il est considéré comme la forme moderne de la logique stoïcienne | W, |
|||||||||||||||||||||||||||||||||||||||||||||
| - S2 T2 (Système ou syntaxe, Théorie) - les connecteurs ¬ , ∧,∨, ⇔, - ou calcul des propositions, -Théorie de la vérifonctionnalité et algèbre de Boole, ou S2 T2 - Lukazievitch a parlé du Calcul des propositions, en nommant ce calcul par les objets de ce calcul, au lieu de l’appeler comme je propose de le faire Calcul de la coordination, en nommant ce calcul par les transformations, les opérations qu’il fait , qu’il accomplit, voyez on passe de la coordination à la proposition en s’intéressant à ce qui est coordonné, par la coordination, vous avez deux types d’objets, comme toujours en mathématiques, c’est ce qui va donner les catégories, vous avez les objets et les flèches, alors ça peut être un couple d’objet, des couples d’objets, vous pouvez faire correspondre par une flèche, une connexion, et il y aura un connecteur qui va connecter les deux lettres, v12.03, et la négation c’est un connecteur binaire par exemple, à un objet on fait correspondre un autre objet par une flèche, on voit bien que les connecteurs sont de l’ordre des flèches, et que les propositions sont de l’ordre des objets, |
||||||||||||||||||||||||||||||||||||||||||||||
| Calcul différentiel | ✔ |
- On appelle dans la haute Géométrie, quantité différentielle ou simplement différentielle , une quantité infiniment petite, ou moindre que toute grandeur assignable. On l'appelle différentielle ou quantité différentielle, parce qu'on la considère ordinairement comme la différence infiniment petite de deux quantités finies, dont l'une surpasse l'autre infiniment peu. Newton et les Anglais l'appellent fluxion , à cause qu'ils la considèrent comme l'accroissement momentané d'une quantité. Leibnitz et d'autres l'appellent aussi une quantité infiniment petite. ( suite sur Chronomath) - Calcul différentiel intégral ou calcul infinitésimal source wiki, une autre approche ici, |
||||||||||||||||||||||||||||||||||||||||||||
Calcul des énoncés ou Calcul des propositions |
✔ |
- c'est le Calcul des Propositions rebaptisé ainsi par Rivenc et Vappereau, car il porte aussi sur les concepts. | ||||||||||||||||||||||||||||||||||||||||||||
Calcul infinitésimal ↑
|
✔ |
- voir calcul différentiel intégral, | ||||||||||||||||||||||||||||||||||||||||||||
Calcul des prédicats de premier ordre↑
L1T1 |
✔ |
- ou calcul des relations, ou logique du premier ordre, ou calcul des prédicats (voir Wiki) Le calcul des prédicats a pour but de définir quels sont les énoncés valides ou non. Deux approches sont possibles : approche sémantique ou approche syntaxique. La théorie des formules de la vérité du calcul des prédicats a été appelé par Tarski sa sémantique. On peut attribuer une valeur de vérité (V ou F) aux formules du langage de ce modèle. - On parle de logique du premier ordre par rapport aux logiques d'ordre supérieures où l'on peut quantifier aussi bien les variables que les prédicats ou les fonctions. La logique du premier ordre introduit des symboles nommés variables, des symboles nommés prédicats (relations), des connecteurs logiques (∧, pour ET; et ∨, pour OU,..) , et deux quantificateurs logiques : l'un universel ∀( pour tout) et l'autre existentiel ∃ (il existe) . - voir Modalités, et Euler Venn; Logique modale, - voir Prédicat , |
Math et schema L, F, L, L2, | |||||||||||||||||||||||||||||||||||||||||||
Calcul des prédicat et des propositions
|
✔ |
- L1T1,(prédicats) lecture des formules kantiques de la sexuation (texte intégral simplifié), 2007, JMV, (Langage, Théorie) - L2T2 (propositions), |
||||||||||||||||||||||||||||||||||||||||||||
Calcul des prédicats de premier ordre kantifié↑ |
- S1 T1 ( Système ou Syntaxe, Théorie) - les connecteurs ∀, ∃, (quel que soit, et Il existe). - les prédicats ce sont les fonctions propositionnelles, ou les concepts, voir Boole et Frege -Théorie de la kantification des prédicats du premier ordre, ou S1 T1 - le calcul en question des propositions traite de la coordination des propositions, et principalement à cette occasion de la théorie de la vérifonctionnalité, (voir ce terme ci-dessous). - Boole veut y faire entrer la syllogistique d'Aristote. |
|||||||||||||||||||||||||||||||||||||||||||||
| Calcul des prédicats monadiques | ✔ |
- prédicat ou concept - (S1 T1) mon, - La syllogistique d'Aristote - Les 14 modes de syllogismes retenus par Aristote, |
||||||||||||||||||||||||||||||||||||||||||||
Calcul des propositions ↑ L2T2 |
✔ |
- P v Q (P ou Q) - En logique mathématique , le calcul des propositions est la première étape dans la définition de la Logique et du raisonnement. Il définit les règles de déduction qui relient les propositions entre elles, sans en examiner le contenu ; il est ainsi une première étape dans la construction du calcul des prédicats , qui lui s'intéresse au contenu des propositions et qui est une formalisation achevée du raisonnement mathématique. source wiki . - le calcul des propositions qu'on devrait plutôt nommer calcul des énoncés (Rivenc et Vappereau) car portant sur des propositions ET des concepts ! -JMV22062010 ENS, L56 - La LCC, in L'amour du tout aujourd'hui, 2 eme partie, JMV, 1992 et annexes 1 et 2 voir aussi Coordination, et Calcul de la coordination L2T2 |
||||||||||||||||||||||||||||||||||||||||||||
Capitonnage |
✔ |
- collapsus, - effet de capitonnage, (JMV09092014, 01.09.42, ), |
||||||||||||||||||||||||||||||||||||||||||||
caractéristique
|
✔ |
- la caractéristique c’est le nombre qui multiplie n’importe quel élément pour donner zéro, {dans 2x = 0, le nombre (2) qui multiplie n’importe quoi pour faire 0, 2 est ici caractéristique, en Algèbre de Boole}. - le nouage et l'enlacement s'efface dans le passage à l'intrinsèque, laissant une trace, sous l'aspect de ces caractéristiques, de ce qu'il y a du nœud, de la chaine Np69 |
||||||||||||||||||||||||||||||||||||||||||||
Cardinal |
✔ |
- nombre Cardinal, W, En linguistique, les nombres entiers naturels zéro, un, deux, trois, etc. s’appellent des adjectifs numéraux cardinaux. En théorie des ensembles, le nombre cardinal ou cardinal d'un ensemble E (fini ou infini) est, intuitivement, le « nombre » d'éléments lui appartenant. On peut définir formellement ce « nombre » comme la classe de tous les ensembles équipotents à E (c'est-à-dire en bijection avec E), ou, de manière fort différente, comme le plus petit ordinal équipotent à E. |
||||||||||||||||||||||||||||||||||||||||||||
Cardinal d'un ensemble |
- nombre des éléments d'un ensemble, compte tenu de l'ordre des éléments. | |||||||||||||||||||||||||||||||||||||||||||||
✔ |
En mathématiques, la cardinalité est une notion de taille pour les ensembles. Lorsqu'un ensemble est fini, c'est-à-dire si ses éléments peuvent être listés par une suite finie, son cardinal est la longueur de cette suite, autrement dit il s'agit du nombre d'éléments de l'ensemble. En particulier, le cardinal de l'ensemble vide est zéro. La généralisation de cette notion aux ensembles infinis est fondée sur la relation d'équipotence : deux ensembles sont dits équipotents s'il existe une bijection de l'un dans l'autre. Par exemple, un ensemble infini est dit dénombrable s'il est en bijection avec l'ensemble des entiers naturels. C'est le cas de l'ensemble des entiers relatifs ou de celui des rationnels mais pas de celui des réels, d'après l'argument de la diagonale de Cantor. L'ensemble des réels a un cardinal strictement plus grand, ce qui signifie qu'il existe une injection dans un sens mais pas dans l'autre. Le théorème de Cantor généralise ce résultat en montrant que tout ensemble est de cardinal strictement inférieur à l'ensemble de ses parties. L'étude de la cardinalité en toute généralité peut être approfondie avec la définition des nombres cardinaux. Il existe plusieurs notations classiques pour désigner le cardinal d'un ensemble, avec l'opérateur Card, le croisillon (#) préfixe, à l'aide de barres verticales de chaque côté ou une ou deux barres horizontales au-dessus |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
 source W, source W, |
||||||||||||||||||||||||||||||||||||||||||||||
Carnap |
✔ |
- voir JMV23092014, 53, (Systèmes formels ou Langage symbolique), La construction logique du monde, La société ouverte et ses ennemis, Le cercle de Vienne. |
||||||||||||||||||||||||||||||||||||||||||||
Catégorie,
|
✔ |
Une catégorie C, se compose de 2 CLASSES : -celle de ses objets et -celle de ses morphismes qui leurs sont associés. Objets et morphismes peuvent être : - des ensembles, les morphismes associés sont les Applications - des espaces topologiques, les morphismes associés sont les Applications continues - les espaces vectoriels, les morphismes associés sont les Applications linéaires - les groupes, les morphismes associés sont les homomorphismes On passe d'une catégorie C à une autre C' au moyen d'un foncteur, associant à tout objet et morphisme de C un unique objet et morphisme de C' |
||||||||||||||||||||||||||||||||||||||||||||
| - voir Théorie des catégories, ci-dessous - voir Consistance, voir Dimension |
||||||||||||||||||||||||||||||||||||||||||||||
| Causalité | ✔ |
- On ne peut pas éviter la causalité, il faut parler de la Cause ! et il ne faut pas essayer d'arranger les choses à la manière pragmatique. JMV20150602, - Causes selon Aristote, gaogoa |
||||||||||||||||||||||||||||||||||||||||||||
| Cercle | ✔ |
- 0, et ronds, - le "docte noeud", |
||||||||||||||||||||||||||||||||||||||||||||
| Cercle de Vienne | - Présentation du Manifeste du Cercle de Vienne, SOULEZ, - Le cercle de Vienne par Malika OUELBANI, Présentation et Table des matières, |
|||||||||||||||||||||||||||||||||||||||||||||
| Le cercle de Vienne, ou Wiener Kreis, est un groupement de savants et philosophes1 qui a fonctionné à Vienne, de 19231 – mais officiellement 1929 sous le nom de Société Ernst-Mach– jusqu'à l'assassinat de son chef de file, Moritz Schlick, le 22 juin 1936, après quoi le club se dispersa. Le Cercle existait de manière informelle déjà avant la Première Guerre mondiale. L’ouvrage de Ludwig Wittgenstein, Tractatus logico-philosophicus (1921), est un des textes de cette époque qui servit de « Bible » à la pensée viennoise. | Wikipedia, suite ... |
 |
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
| - CARNAP sur gaogoa, | ||||||||||||||||||||||||||||||||||||||||||||||
| - La construction logique du monde, CARNAP.Rudolf, ou Der logische Aufbau der Welt, Vrin,1928, 1998, 2002, |
Table des matières sur gaogoa |
|||||||||||||||||||||||||||||||||||||||||||||
| Chaine (lettre et noeud) |
✔ |
- voir Entrelacs, Noeuds, Tresses, Chaines, Echeveau, sur gaogoa, - un discours qui se tient, qui est enchainé, c’est là que la notion de chaine va apparaître en tant qu’elle représente l’effectivité, de quelque chose d’effectif, qui tient, quand on tire dessus dans tous les sens, ça tient, et c’est ça qui fait, c’est ce que moi j’appelle effectivité, et que j’oppose à la réalité qu’on voudrait nous imposer, surtout de plus en plus, du fait, c’est pas seulement du fait de l’influence du Cercle de Vienne, et du logico positivisme, même avant Russel, il faisait déjà du logico-positivisme, Bertrand Russell, donc la question de l’effectivité, en allemand, au début des Ecrits, vous verrez ça, Lacan en parle dans ses antécédents, il souligne cette différence chez Freud entre Realitad et Virtsgeigt et le virlitsgeit, c’est deux manière de parler de la réalité, et Virtgeigt, il y en a une qui s’appelle effectivité, je propose de le traduire par effectivité, si on fait quelque chose effectivement, peut être y-a-t-il du mensonge, mais pourquoi le mensonge ne serait pas lui-même effectif, le mensonge c’est bien lié au fait de dire, et ça a une effectivité le fait de dire, c’est même la fonction phallique, par excellence, JMV23062015 - Le nœud des mathématiciens est un plongement de cercle, c'est un cercle. W, |
||||||||||||||||||||||||||||||||||||||||||||
Chaîne borrroméenne ↑ |
✔ |
- Le nœud ou fausse chaîne où chaque rond se noue aux autres ronds sans emprunter le trou des autres ronds. Chaque rond n'entre dans le trou d'un autre rond qu'à en ressortir ensuite en suivant son trajet Essaim p 128. C'est la propriété borroméenne. 3333-3333, , - Dans le nœud borroméen le nœud en tant que principe, en tant qu'ordre, par quoi toute la chaine-nœud subsiste ne réside pas dans un rond, mais y réside tout de même . Car à ôter un rond, les ronds de la chaîne sont libres . |
||||||||||||||||||||||||||||||||||||||||||||
Chainette borroméenne à homotopie près |
✔ |
- "ça claque" p 55, Le noeud de Soury vient d'une chaine borroméenne à quatre de la suite des borroméens, suite issue deu premier protoype, formant les chaînes étudiées par Finke, finkéennes ou dites aussi par Soury : chainettes borroméennes à homotopie près. Soury utilise les chainettes de manière montante et non descendante ! p56 |
||||||||||||||||||||||||||||||||||||||||||||
Chaînes bruniennes |
✔ |
- ( autre nom pour les chainoeuds borroméens ) à propos du borroméen généralisé, il s'agit de la généralisation des chaînes bruniennes, esquissée par Debrunner et achevée par Penney, chaines où il suffit de retirer un nombre fixé de ronds quelconque pour défaire une chaine. Pour le borroémen, c'est 1 rond. "ça claque" p 47, pour une chaine de 5 ronds, en oter 2 pour trivialiser le noeud, serait une généralisation. | ||||||||||||||||||||||||||||||||||||||||||||
Chaine de David |
✔ |
- Chaine dite de "David", ou Hexagramme, 222-66, ( Discours liés à la Surfaces du non-noeud... non exhaustivement) - Si mise en continuité des 2 anneaux, alternés, celà produit le noeud propre 22222-55, dit Pentagramme étoile, noeud torique. |
||||||||||||||||||||||||||||||||||||||||||||
Chaînes Fichéennes↑ |
✔ |
- "ça claque" p 55, Le noeud de Soury vient d'une chaine borroméenne à quatre de la suite des borroméens, suite issue deu premier prototype, formant les chaînes étudiées par Finke, finkéennes ou dites aussi par Soury : chainettes borroméennes à homotopie près. |
||||||||||||||||||||||||||||||||||||||||||||
chaine signifiante (la) ↑ |
✔ |
- la chaine signifiante : anneaux dont le collier se scelle sur l'anneau d'un autre collier fait d'anneaux. - Le collier fait d'anneau d'une chaîne peut être enveloppé dans un tore. (Conséquence de la définition de la chaîne signifiante de Lacan les 14-26 mai 1957 !!! ci-dessus) (voir chaines Fichéennes) |
||||||||||||||||||||||||||||||||||||||||||||
Chainoeud↑
|
✔ |
- linknots, ou Noeud impropre, pour les chaines à coupure constantes, exemple du Noeud borroméen avec ses quatre coupures. Ces chainoeuds ne contiennent aucun enlacement. Noeud p109 | ||||||||||||||||||||||||||||||||||||||||||||
| Chomsky | ✔ |
- Chomsky a montré que la langue anglaise n’était pas à l’état fini, on ne pouvait pas la mécaniser, c’est un produit du langage, c’est un produit détaché du langage, et tout ces gens confondent les mathématiques avec leurs calculs, ça c’est l’erreur qu’il faut que vous appreniez à éviter, Lacan en parle dès la Lettre volée, Lacan le dit : on confond toujours les mathématiques avec leurs calculs et les mathématiciens avec leurs calculs, que les calculs puissent être autonomisés d’une manière mécanique dans certains cas favorables quand c’est récursif, quand c’est heureusement récursif, que Chomsky ait montré que les langues étaient seulement semi récursives, les langues comme l’anglais et que c’était pas mécanisable intégralement et qu’on ne peut en mécaniser qu’une portion, des petits bouts, des localités, donc toutes ces choses sont des choses élémentaires qui aujourd’hui seraient parait-il à l’ordre du jour, d’après les gens sérieux, les psychothérapeutes français devraient pour pratiquer une psychothérapie, déjà moi je trouve que c’est assez hasardeux, de pratiquer des psychothérapies, mais ils devraient avoir une formation qui fait qu’ils connaissent aussi bien les neurosciences, ça c’est le côté vitalise biologie médical, les neurosciences que le cognitivisme que la psychanalyse, mais on se moque du monde ça n’a rien à voir, car la psychanalyse elle s’occupe de la langue, et du langage, la différence que je fais entre la langue et le langage, c’est qu’il y a des langues et je tiens qu’il n’y a pas des langages, ça c’est une des faiblesses du discours des logiciens, et que vous voyez que même Lacan reprend dans sa formule célèbre que l’inconscient est structuré comme un langage (une langue pour JMV), mais il s’en explique, il n’a pas pu se retenir d’employer le comme un langage, dans comme un il y a commun, ça veut dire que l’inconscient est structuré comme du langage commun, comme du langage banal, peut être que ça a à voir avec le Nom du père, JMV19012010, - L'étude la linguistique doit surmonter les deux épreuves de son enterrement en grandes pompes ! La première due à Chomsky (1, 2) qui reprend les grammaires chomskyennes de Carnap, ( Structure syntaxiques et théorie des traces, puis gouvernement et liage ! ) et stope net les recherches en linguistique, ce qu'il viendra marteler pour les sourds au Collège de France (entre autre) du 28 au 31 mai 2010. et la seconde épreuve (l'à Mort du Signe), du côté de chez Saussure, qui revient à la représentation du Signe Saussurien, entre Signifiant et signifié, alors qu'il faudrait revenir au PHONEME découvert par Baudouin de Courtenay, or c'est pas le signal qui compte, pas la phonétique, mais le son, le signifiant, ça se passe du côté des oreilles. Il faut se tourner vers la phonologie, du côté de chez Troubetskoï, et ses "Principes de phonologie". (à préciser, à développer) - Voir gaogoa, Linguistique & Bibliographie & Biographie, |
||||||||||||||||||||||||||||||||||||||||||||
| (remarque du scrib : Notons que J-Y.GIRARD a publié : TURING Alan,voir TURING ci-dessous, La machine de Turing, Sciences, S131, Points, 1991, 1995), | ||||||||||||||||||||||||||||||||||||||||||||||
| Clinique | ✔ |
- Ce qui importe dans les Noeuds : chaînes ou noeud propre, c'est s'il y a ou pas du noeud ! (noeud / enlacement) (ex : le noeud borroméen, a 1 noeud et 0 enlacement ! aussi n'est pas vraiment un noeud, il est improprement dit ..., ou chainoeud, ) - voir Structure, Nosographie, Théorie de l'asile, Structures freudo-lacanienne du symptôme, Treillis, - Clinique du processus du neuds, JMV, 12-12-2014 |
||||||||||||||||||||||||||||||||||||||||||||
| Classe | ✔ |
- Les classes sont ausi appelées ensembles. Une branche spéculative des mathématiques appelée théorie des ensembles est issue de l'oeuvre de Cantor. Elle s'occupe des problèmes de l'infini et traite des classes dans une perspective réaliste qui ne peut en aucun cas en être écartée comme une simple façon de parler à l'instar de l'algèbre booléienne des classes. Le terme "ensemble" tend à être préféré à celui de "classe", exception faite d'un certain contexte technique où la double terminologie est utilisée pour marquer une distinction particulière. Dans les mathématiques modernes des "classes secondaires", la dénomination élargie de théorie des ensembles est confusément appliquée à l'autre extrémité de l'échelle : à l'algèbre booléienne des classes, donc en réalité à la simple logique des termes généraux. in Méthode de Logique, Quine. |
||||||||||||||||||||||||||||||||||||||||||||
- En mathématiques, la notion de classe généralise celle d'ensemble. Ce n'est pas forcément le cas d'une classe, qui est une collection d'objets que l'on peut définir, dont on peut donc parler, mais qui ne forme pas nécessairement un ensemble. Quand une classe n'est pas un ensemble, elle est appelée classe propre. Elle ne peut alors pas être élément d'une classe (ni, a fortiori, d'un ensemble). Les paradoxes de la théorie des ensembles, comme le paradoxe de Russell, montrent la nécessité d'une telle distinction. Ainsi la propriété « ne pas appartenir à soi-même » (x À l'aube du XXe siècle, certains logiciens et mathématiciens comme Ernst Schröder, Giuseppe Peano ou Bertrand Russell emploient le terme « classe » la plupart du temps pour ce qui est appelé aujourd'hui « ensemble »1. Cet usage perdure dans certains cas particuliers. Ainsi pour la notion usuelle de relation (dont le graphe est un ensemble de couples), une classe d'équivalence est un ensemble. Si on élargit aux classes propres, on ne peut plus parler d'ensemble quotient. Parfois les deux termes sont employés pour améliorer la clarté d'expression : dans certains contextes, on peut préférer parler de classe d'ensembles plutôt que d’ensemble d'ensembles sans y attacher un sens particulier. |
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
| Cogito cartésien, | planche, en lien à la Structure Logique du Sujet divisé, source cours de JMV du mardi 15 juin 2010, 3 planches, | |||||||||||||||||||||||||||||||||||||||||||||
| Cogitatur Lacanien | planche, en lien à la Structure Logique du Sujet divisé, source cours de JMV du mardi 15 juin 2010, 3 planches, | |||||||||||||||||||||||||||||||||||||||||||||
| Cloture algèbrique | ✔ |
- En mathématiques, une clôture algébrique d'un corps commutatif K est une extension algébrique L de K qui est algébriquement close, c'est-à-dire telle que tout polynôme de degré supérieur ou égal à un, à coefficients dans L, admet au moins une racine dans L.
Une clôture algébrique d'un corps K peut être vue comme une extension algébrique maximale de K. En effet, il suffit de remarquer que si L est une extension algébrique de K, alors une clôture algébrique de L est également une clôture algébrique de K, donc L est contenu dans une clôture algébrique de K. exemples : D'après le théorème fondamental de l'algèbre, le corps des nombres complexes est une clôture algébrique du corps des nombres réels. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
analyse Combinatoire↑ |
✔ |
- En mathématiques, la combinatoire, appelée aussi analyse combinatoire, étudie les configurations de collections finies d'objets ou les combinaisons d'ensembles finis, et les dénombrements. - ou analyse combinatoire, En mathématiques , la combinatoire étudie les configurations de collections finies d'objets ou les combinaisons d' ensembles finis , et les dénombrements. (source wiki) |
sur wiki |
|||||||||||||||||||||||||||||||||||||||||||
| Un résultat de combinatoire plus sophistiqué, remontant à l'Antiquité grecque, est attesté par l'anecdote suivante : Plutarque rapporte, dans les Propos de table, une assertion de Chrysippe « contredite par tous les mathématiciens, et entre autres par Hipparque », sur le nombre de façons de combiner dix propositions. Hipparque savait que le nombre de « propositions composées positives » que l'on peut former à partir de dix propositions simples est 103 049, et que le nombre de propositions négatives est 310 952. Cette affirmation est restée inexpliquée jusqu'en 1994, quand David Hough, un étudiant de l'université George-Washington, observe qu'il y a 103 049 façons de parenthéser une suite de dix éléments. Une explication semblable peut être donnée pour le deuxième nombre : il est très proche de (103 049 + 518 859)/2 = 310 954, qui est la moyenne des dixième et onzième nombres de Schröder-Hipparque, et qui compte le nombre de parenthésages de dix termes avec un signe. |
||||||||||||||||||||||||||||||||||||||||||||||
| - voir jeux... | ||||||||||||||||||||||||||||||||||||||||||||||
| Commutatif, | ✔ |
- En mathématiques, et plus précisément en algèbre générale, une loi de composition interne * sur un ensemble S est dite commutative lorsque, pour tous x et y dans S, |
W, |
|||||||||||||||||||||||||||||||||||||||||||
corps commutatif, ou anneau commutatif, |
En mathématiques, un corps commutatif (parfois simplement appelé corps, voir plus bas, ou parfois appelé champ) est une des structures algébriques fondamentales de l'algèbre générale. C'est un ensemble muni de deux opérations binaires rendant possibles les additions, soustractions, multiplications et divisions. Plus précisément, un corps commutatif est un anneau commutatif dans lequel l'ensemble des éléments non nuls est un groupe commutatif pour la multiplication. Selon la définition choisie d'un corps qui diffère selon les auteurs (la commutativité de la multiplication n'est pas toujours imposée), soit les corps commutatifs sont des cas particuliers de corps (dans le cas où la commutativité n'est pas imposée), soit la dénomination corps commutatif est un pléonasme qui désigne simplement un corps (dans le cas où elle l'est). On renvoie à l'article corps (mathématiques) pour plus de détails. Des exemples élémentaires de corps commutatifs sont le corps des nombres rationnels noté La théorie des corps commutatifs est le cadre historique de la théorie de Galois, une méthode d'étude qui s'applique en particulier aux corps commutatifs et aux extensions de corps, en relation avec la théorie des groupes, mais s'étend aussi à d'autres domaines, par exemple l'étude des équations différentielles (théorie de Galois différentielle), ou des revêtements. |
W, |
↑ | |||||||||||||||||||||||||||||||||||||||||||
Commutateur ↑
|
✔ |
- zone la plus centrale dans la composition de deux ronds (en situation de faux trou). P133. |
||||||||||||||||||||||||||||||||||||||||||||
✔ |
- Liste des principaux concepts de logique générale (W), de logique mathématique (W), de logique classique (W), - Ecrits logiques et philosophiques, G.FREGE, Vrin, 1971, & C.IMBERT, .pdf, |
F, Idéographie, Techno-science,
|
||||||||||||||||||||||||||||||||||||||||||||
Condensation |
✔ |
- C'est ce qui "ne cesse de ne pas s'écrire" dès la condensation irréversible, et irréductible au service du refoulement primordial, (Urverdräng) préalable à la signifiance du sujet, soit des "raisons" qui n'en sont pas encore à jouer du repésentant. "ça claque" p61, | ||||||||||||||||||||||||||||||||||||||||||||
Congruence↑ |
✔ |
- Sous le terme de congruence se cachent des notions semblables mais de niveaux d'abstraction différents. Historiquement, la notion de congruence sur les entiers relatifs a été introduite par Gauss vers 1801. Arithmétique des congruences ou modulaire. Voir Théorie des congruence sur Chronomath, :.. La relation ≡ est une relation d'équivalence . L'ensemble des classes d'équivalence constitue l' anneau des classes résiduelles modulo p . (≡ pour congruence..) |
||||||||||||||||||||||||||||||||||||||||||||
Coniques↑ |
✔ |
- Les coniques, W, - Desargues, W, - La géométrie projective, gaogoa, (es), - Le DI, la droite infinie, 2006, J-M.V |
||||||||||||||||||||||||||||||||||||||||||||
Connecteur |
✔ |
- Treillis des connecteurs logiques binaires, tentative d'écriture en live, du JMV27012015 .pdf, - Connecteurs logiques, connecteurs propositionnels classiques: la liste de tous les connecteurs, d’abord avez-vous l’idée que les connecteurs logiques, si vous avez les deux unaires, x et x + 1 ou x et ¬ x, vous avez des connecteurs binaires, et il y en a combien, il y en a 16 !, si vous avez 16 connecteurs binaires, avec les connecteurs binaires et les connecteurs unaires, vous pouvez construire tous les connecteurs trinaires, il y a des gens qui sont tout à fait stupides et nuls en mathématique, ils commencent à se proposer comme exercice de faire la liste de tous les trinaires, j’ai connu plusieurs de ces auditeurs et des collègues faire cet exercice, il y en a 500 (cinq cents et quelques) des trinaires, c’est sans intérêt, l’intérêt c’est de voir qu’il y en a 16 binaires, et que dans les binaires il y en a déjà des unaires qui font partie des binaires - construction des connecteurs logiques, tentative du JMV27012015, (lien ci-dessus), exercice de haute voltige, sans filet ... - En logique, un connecteur logique est un opérateur booléen (variable à deux états, binaire) utilisé dans le calcul des propositions. Comme dans toute approche logique, il faut distinguer un aspect syntaxique (fonction) et un aspect sémantique. (sens) D'un point de vue syntaxique, les connecteurs sont des opérateurs dans un langage formel pour lesquels un certain nombre de règles définissent leur usage1, au besoin complétées par une sémantique. sur wikipedia, |
||||||||||||||||||||||||||||||||||||||||||||
Conscience ↑ |
✔ |
- - Wundt, Langage, sur gaogoa, - Conscience et non conscience, Inconscient, (voir ce mot) - La double lecture, (à minima !), Cas MAJORITAIRE des langues à tons dans le monde ! W, ce qui justifie la remarque que les Japonnais ne sont pas des candidats à l'Analyse ! Les Kanji sont des idéogrammes d'origine chinoise importés au 5ème siècle. Chaque Kanji possède 2 lectures : On-Yomi qui est la lecture chinoise, et Kun-Yomi, qui est la lecture japonaise. Voir aussi la Langue chinoise, W, aussi Hangeul, - l'amour du tout, partie 3, 1992, JMV - Freud, ...Cs : . « ne se peut ni expliquer, ni décrire. Cependant, lorsqu'on parle de conscience, chacun sait immédiatement par expérience de quoi il s'agit » l'acte psychique qui permet le devenir conscient est soutenu par l'attention, fonction psychique sur laquelle il insiste à plusieurs reprises, remarquant sa nécessité en raison de la fugacité spontanée de la conscience. L'orientation de l'attention favorise le passage vers le conscient des représentations préconscientes, tout autant que l'énergie investie dans lesdites représentations. L'inconscient, quant à lui, « ne peut en aucun cas devenir conscient » en dehors du travail de la cure, qui doit permettre la prise de conscience du refoulé. ...suite sur ....carnet psycho, - Lacan, Il avance en partant de la critique du cogito que « ce qui pense est barré de la conscience et que le sujet qui parle, c'est le sujet de l'inconscient » Lacan ne néglige pas la conscience mais il en dénonce les illusions. Pour lui, la conscience n'est pas connaissance mais mé-connaissance, où il joue sur le double sens du mé. En outre, il ne laisse pas la perception dans son statut freudien de pur filtre. Il la structure en la liant au symbolique, car à quoi servirait le perçu s'il n'était pas nommé? Quant au désir, étant en grande partie inconscient, il échappe dans cette mesure à la conscience..... suite sur carnet psycho, - Lettre 52 & Schémas R, L, F, |
||||||||||||||||||||||||||||||||||||||||||||
Consistance↑ |
✔ |
- Consistance, 1, 2, (pour Lacan), - Pour LeRobert !, |
||||||||||||||||||||||||||||||||||||||||||||
Continu↑ |
✔ |
- Ce terme définit ce qui relève de la topologie. C'est à la topologie générale nommée aussi topologie ensembliste que revient la charge de définir les applications continues. Elle donne donc son cadre à la topologie dans son ensemble. Essaim p 27. Les applications continues dépendent de la définition des espaces topologiques, de ce que nous appelons une topologie. Ce n'est pas réalisé dans l'analysis situs. La véritable topologie ne cerne ses objets quéà partir des invariants préservés par des transformations, ici continues, comme en toute catégorien d'objet mathématique. Essaim,
|
||||||||||||||||||||||||||||||||||||||||||||
| Continuité, | ||||||||||||||||||||||||||||||||||||||||||||||
Controle |
✔ |
- c’est que vous pouvez conquérir avec la psychanalyse une indépendance, alors que vous voyez que la psychanalyse se transforme en soumission volontaire, tous ces gens qui sont en contrôle toute leur vie, le fait qu’à Paris on vous dit que n’importe qui peut pratiquer l’analyse s’il est en contrôle, c’est un scandale, ça veut dire que la cure ne sert à rien ! Faire une analyse c’est se donner les moyens de devenir un analysant infini, et c’est la condition pour être dans le fauteuil ! JMV20150602 - La psychanalyse est une prophylaxie de la dépendance ! |
||||||||||||||||||||||||||||||||||||||||||||
Coordination ↑ S2T2 |
✔ |
- La coordination elle porte aussi bien sur les Prédicats que sur les Propositions, dans le calcul des Prédicats, JMV20150602, - Il y a deux relations dans les propositions, la subordination et la coordination, et Grevisse il dit coordination parce que dans un traité de logique, la coordination est traitée en logique, alors que la subordination elle est traitée en grammaire, cela montre qu’il y a une proximité entre la logique et la grammaire, vous voyez que la logique au niveau de la coordination, c’est de la grammaire, mais les grammairiens abandonnent ça aux logiciens parce que, il y a une histoire de vérité qui va apparaître, un calcul sur le Vrai et le Faux. - Clef pour la passe, 1ere partie, argument 3, dans L'amour du tout, JMV, aspect modal de la logique de la coordination - Clef pour la passe, 2 eme parie, dans L'amour du tout, JMV, effet sur le calcul de la coodination - les deux régimes de la coordination, JMV20150602, p13, 14, 15 |
F, |
|||||||||||||||||||||||||||||||||||||||||||
| Corollaire | ✔ | - Résultats que l’on doit démontrer également et qui découlent d’un théorème qui les précède (une sorte de conséquence),(L.PUJO-MENJOUET_Fonfamentaux,) | ||||||||||||||||||||||||||||||||||||||||||||
| Corps, | ✔ |
- I, Imaginaire, le corps, c'est l'imaginaire, la dimension deux, 2 - Le tore c'est le corps ! - La surface du tore est de dimension 2, alors que son volume s'inscrit dans la dimension 3 |
||||||||||||||||||||||||||||||||||||||||||||
| Corps, | ✔ |
- Groupe, anneaux, corps et module, algèbre, espace vectoriel ! donc moi je vous propose de noter que vous avez pour l’instant la notion de groupe, et la structure linéaire qui accompagne les groupes ça s’appelle module , vous avez ensuite les anneaux, et la structure linéaire qui accompagne les anneaux ça s’appelle Algèbre, vous avez les corps, et la structure linéaire qui accompagne les corps ça s’appelle les espaces vectoriels, et on les connait bien ceux là, les espaces vectoriels, parce que ça sert en géométrie, avec les vecteurs, c’est pour ça que ça s’appelle espace vectoriel, on a appris ça en mécanique, celle de Newton, la mécanique se fait dans un espace vectoriel, JMV27012015 |
||||||||||||||||||||||||||||||||||||||||||||
| Corps de Galois | ✔ |
- Mais ici nous allons nous apercevoir que nous allons utiliser les termes de module pour les groupes, algèbre pour les anneaux, et espace vectoriels pour les corps, et que ça permet de distinguer ce que nous allons faire, et ce qu’a fait Guitart, qui lui est parti de ce corps là, et voilà ce qu’il a fait, il a construit : l’algèbre de Boole, c’est ce que je suis en train d’essayer de construire, 1.22.34, et puis il a construit aussi les espaces vectoriels, qui s’appellent les corps de Galois, et qui ne sont pas très compliqués à construire puisqu’ils sont, ont les écrit comme ça, GF(2n) ; ça veut dire pour un anglais Galois Fields 2n, et ce qu’il a montré c’est qu’il y avait une corrélation entre les deux, ce qui fait que c’est la première fois à ma connaissance, mais à la connaissance des mathématiciens, qu’on établit une relation entre Galois et Boole, JMV27012015 | ||||||||||||||||||||||||||||||||||||||||||||
| Corps parfait, | ||||||||||||||||||||||||||||||||||||||||||||||
| Corps premier, | ||||||||||||||||||||||||||||||||||||||||||||||
| Corps symbolique | ✔ |
- Le corps du symbolique de s'incorporer au corps propre, le fait corps. Etoffe p28 | ||||||||||||||||||||||||||||||||||||||||||||
| Coupure | ✔ |
- Noeud coupure : Ce sont des noeuds alternés dont tous les croisements sont traversés par une coupure. Noeud p 167. ( C'est le cas du Trefle ou de la famile des Trèfles) - c'est ce que doit tracer l'interprétation du nœud (plusieurs coupures, donc autant d'interprétations) Np78, - la coupure qui condense la désorientation de la surface, au désir, est identifiée à une métonymie (E a' 21, p601) Np69 -Nombre de la coupure k : la coupure passe par un certain nombre de demi torsion, ce nombre est le nombre de la coupure noté k, Np78 - pour une chaine faite de plusieurs ronds il y a plusieurs coupures possibles. Si le nombre de ronds est noté r, le nombre de coloriage possibles est 2 r , et le nombre de la coupure k est 2 r-1 . Ces différentes coupures ont la même parité (pair pour la famille des des Listing ou impair pour les famille des Trèfles – que ce soit un nœud propre ou une chaine !). K est le nombre de demi torsion, ou le nombre de croisements par où passe la coupure.Np76 |
||||||||||||||||||||||||||||||||||||||||||||
| - Topologie de la coupure, comment se fabrique la coupure . - Notion de "petite coupure" et de " grande coupure". - L'articulation des coupures compose la structure. Le noeud est coupure(s), est Structure ! - Trou coupure, 2, |
||||||||||||||||||||||||||||||||||||||||||||||
| - Coupure et cure, Cure & noeuds, | ||||||||||||||||||||||||||||||||||||||||||||||
| Critique | ✔ |
- qu'est ce qu'une critique : c'est pas l'incrédulité,
pour critiquer un auteur il faut lui faire confiance, et pister des coupures où on va pouvoir introduire un commentaire, et le meilleur commentaire que l'on puisse faire de quelqu'un qui a une pratique c'est de pratiquer, un instrument, l'écriture, les mathématiques, ... - c'est l'idée de la critique transcendantale , c'est l'idée de la structure même du langage, en tant qu'il n'y a pas de métalangage, c'est qu'il y a du métalangage, mais cela n'en est pas, alors c'est difficile à comprendre pour un occidenté, c'est que le processus critique, la meilleur c'est celle de Kant, c'est la seule chose qu'on pourra retenir de Kant, la critique transcendantale, ce n'es pas transcendant, c'est pas le dépassement, c'est juste que nous avons une relation avec un objet, et j'ai une relation à la relation que j'ai avec cet objet, c'est-à-dire que je peux faire un commentaire, et si je fais un bon commentaire qui rejoint l'objet, si je joue de la musique, et si quelqu'un trouve que ce que je fais rejoint la musique, alors la critique va fonder la musique, JMV09092014 ; ..... il y a l'arithmétique qui s'écrit et la théorie des nombres que vous êtes en train de faire, qui est un commentaire, et quand vous écrivez quelque chose sur les nombres vous écrivez un nombre, ce qui fait que vous allez produire un effet de ce que Lacan appel un capitonnage , 01.09.42, un collapsus, ça va se rejoindre, c'est le principe de la critique transcendantale de Kant, JMV09092014; |
||||||||||||||||||||||||||||||||||||||||||||
Croisement ↑ |
✔ |
- il existe deux types de croisements selon qu'il s'agit du croisement de deux composants de ficelle localisables dans le trajet de deux ronds distincts pour les croisements impropres, ou du même rond pour les croisements propres. (Théorie des non-nœuds entiers, site JMV) |
||||||||||||||||||||||||||||||||||||||||||||
Cross-cap↑ |
✔ |
- Cross cap, lutecium, Définitions, Assertions, Mathematas, - Plan projectif en cross-cap, sur Lutecium, J.S, - Cross-cap et surface de Boy, VALAS, - cross-cap, - objet a et cross-cap, bibliographie gaogoa, - animation, - Moebius et cross-cap, -voir Plan projectif, Noeud p303 - voir Plan projectif, - Clinique du processus du neuds, JMV, 12-12-2014 |
||||||||||||||||||||||||||||||||||||||||||||
| CURRY-HOWARD | ✔ |
- N'est pas (encore !) un homard au curry ! ça tient à peu , juste deux quarts de tour et c'est QI !!
- La correspondance de Curry-Howard, appelée1 également isomorphisme de Curry-de Bruijn-Howard, correspondance preuve/programme ou correspondance formule/type, est une série de résultats à la frontière entre la logique mathématique, l'informatique théorique et la théorie de la calculabilité. Ils établissent des relations entre les démonstrations formelles d'un système logique et les programmes d'un modèle de calcul. Les premiers exemples de correspondance de Curry-Howard remontent à 1958, date à laquelle Haskell Curry remarqua l'analogie formelle entre les démonstrations des systèmes à la Hilbert et la logique combinatoire, puis à 1969 où William Alvin Howard remarqua que les démonstrations en déduction naturelle intuitionniste pouvaient formellement se voir comme des termes du lambda-calcul typé. La correspondance de Curry-Howard a joué un rôle important en logique, car elle a établi un pont entre théorie de la démonstration et informatique théorique. On la retrouve utilisée sous une forme ou une autre dans de très nombreux travaux allant des années 1960 à nos jours : sémantique dénotationnelle, logique linéaire, réalisabilité, démonstration automatique, etc. |
- source W, - source w, Fonctionnel Formel, |
|||||||||||||||||||||||||||||||||||||||||||
| - Recherche sur la théorie de la démonstration, HERBRAND.Jacques, 1930, | ||||||||||||||||||||||||||||||||||||||||||||||
| - Théorie de la démonstration, GIRARD.Jean-Yves, | ||||||||||||||||||||||||||||||||||||||||||||||
| D | ||||||||||||||||||||||||||||||||||||||||||||||
David |
✔ |
- Noeud de David, ou Hexagramme, 222/66, 222/44, 22/22, Chaine de David et Pentagramme, | ||||||||||||||||||||||||||||||||||||||||||||
Debrunner
|
✔ |
- De Brunn à Debrunner, | ||||||||||||||||||||||||||||||||||||||||||||
| Définition | ✔ | C'est donner un nom à un objet ou un concept vérifiant une certaine propriété non encore introduite en mathématique.(L.PUJO-MENJOUET_Fonfamentaux,) | ↑ | |||||||||||||||||||||||||||||||||||||||||||
Degré |
✔ |
Le degré des problèmes en mathématique : - Le premier degré est un problème ( linéaire) qui peut se mettre en équation et où l'inconnue, x, vérifie une équation du type ax + b = 0, et s'il y a plusieurs inconnues x, y, z, quelles vérifient un système de telles équations. Equation d'une droite passant par l'origine : y = ax. Equation d'une droite ne passant pas par l'origine : ax +by + c = 0 Les problèmes linéaires concernent l' addition et la multiplication par un nombre et le parrallélisme et la proportionnalité. - Le second degré, résoud les problèmes non linéaires, soit un problème qui peut se mettre en équation de telle manière que l'inconnue x vérifie une équation du type ax² + bx + c = 0. Second degré du fait que l'inconnue a une puissance égale à deux ! Il peut y avoir plusieurs inconnues avec des puissances de 2 ! Le second degré traduit les questions de mesures et de distances. |
||||||||||||||||||||||||||||||||||||||||||||
Demande |
✔ |
- la coupure est un composé de deux tours longitude et d’un tour méridien, je vous explique tout de suite ce que je veux dire, (figure du tore central dans les schémas), vous avez les tours longitudes comme ça, et le tour méridien comme ça, pour obtenir la coupure qui définie la bande de moebius, c’est deux tours longitudes et un tour méridien, V01-32.54 ; 39.20, mais vous pouvez aussi faire le bande de moebius si vous retournez le tore comme une crêpe ou comme une sphère que vous retournez, vous pouvez l’obtenir par deux tours méridiens et deux tours longitudes, ( ?), ça c’est ce que Lacan va faire pour parler dans l’Étourdit de la même chose que dans l’Identification, mais en le disant à l’envers, de 1961 à 1974, dans l’Étourdit il dit la même chose que ce qu’il a dit de ce qu’il appelle le tour de la demande et le tour du désir, il le dit d’une manière inversée dans l’Étourdit, puisqu’il définit le tour de la demande comme le tour longitude et le tour du désir comme méridien, JMV16062015, | ||||||||||||||||||||||||||||||||||||||||||||
| Démonstration | ✔ | En mathématiques et en logique, une démonstration est un ensemble structuré d'étapes correctes de raisonnement. Dans une démonstration, chaque étape est soit un axiome (un fait acquis), soit l'application d'une règle qui permet d'affirmer qu'une proposition, la conclusion, est une conséquence logique d'une ou plusieurs autres propositions, les prémisses de la règle. Les prémisses sont soit des axiomes, soit des propositions déjà obtenues comme conclusions de l'application d'autres règles. Une proposition qui est la conclusion de l'étape ultime d'une démonstration est un théorème. Le terme « preuve » est parfois employé comme un synonyme de démonstration par attraction de l'anglais proof. La démonstration est foncièrement différente de l'argumentation, qui est une autre forme de raisonnement, employant des arguments qualitatifs, en faisant référence éventuellement à des données chiffrées, dans le but de pousser quelqu'un à agir. |
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
Dans le style de Fitch pour la déduction naturelle, une démonstration est « une suite finie de formules dont chacune est soit un axiome, soit une conséquence immédiate des formes précédentes en vertus d'une règle d'inférence »3. De manière générale, une démonstration est un « raisonnement qui permet d'établir une proposition4 ». Dans son documentaire consacré au dernier théorème de Fermat5, Simon Singh demande à des mathématiciens parmi lesquels John Conway, Bary Mazur, Ken Ribet, John Coates, Richard Taylor de préciser la notion de démonstration en mathématiques. Ils proposent, informellement : « suite d'arguments basée sur des déductions logiques, qui découlent les unes des autres, étape par étape, jusqu'à ce que vous établissiez une preuve rigoureuse ». |
||||||||||||||||||||||||||||||||||||||||||||||
| voir Théorie de la démonstration, ci-dessous, | ||||||||||||||||||||||||||||||||||||||||||||||
| De Morgan | - lire ci-dessous : De MORGAN; - Lois de De Morgan : idem ci-dessous, |
|||||||||||||||||||||||||||||||||||||||||||||
| Dérivation, | ||||||||||||||||||||||||||||||||||||||||||||||
| Désir | ✔ | - Chez Lacan, selon Wikipedia, Ce qui est visé dans le désir c’est donc la jouissance, i.e. une présence immédiate, une complétude que Lacan, après Freud, nomme La Chose (das Ding), autrement dit cela qui ne peut être nommé. L’homme étant parlant, son désir ne peut se faire que sur le mode symbolique du langage, par conséquent, il ne peut jamais atteindre l’objet de sa jouissance ; autrement dit, parce que sa jouissance se porte sur des objets phénoménaux qui ne sont pas à proprement parler l’objet du désir (objet a), il ne peut qu’être confronté à l’insatisfaction. Mais cette insatisfaction permet alors de relancer le désir en l’homme, c'est-à-dire que si La Chose était quelque chose dont on pouvait jouir, il n’y aurait plus de désir. La jouissance est donc bien visée dans le désir, mais elle demeure inatteignable, mieux, interdite. La Chose est en effet une béance qui fait que chaque objet est insatisfaisant. Ainsi après la jouissance de chaque objet, le désir est donc relancé vers un autre par la dynamique dont procède La Chose, elle est donc entre deux objets du désir, ces deux objets qui ne peuvent être que « dits » : elle est inter-dite. Ce vide impénétrable de La Chose, ce manque perpétuel est donc constitutif du désir. suite sur wikipedia, - Selon M.SIBONI, - Cupidon dans la mythologie grecque, gaogoa, |
↑ | |||||||||||||||||||||||||||||||||||||||||||
| Diagramme d'Euler-Venn↑ | ✔ |
- un diagramme d'Euler-Venn c'est quelque chose qui correspond aux Tables de Vérité. - Voir Syllogismes, ARISTOTE, Organon, |
||||||||||||||||||||||||||||||||||||||||||||
Diagrammes d'EULER, de VENN et de CARROLL Les diagrammes d'Euler, de Venn et de Carroll sont des schémas géométriques utilisés pour représenter des relations logico-mathématiques. Créés pour visualiser la structure logique des syllogismes, ils sont couramment utilisés pour l'étude des relations entre ensembles.
|
W, |
|||||||||||||||||||||||||||||||||||||||||||||
| - 08 septembre 2009,, 181, j’ai trouvé le type 181 d’écritures algébriques qui permet de lire au travers de diagrammes logiques la 182 topologie de Lacan dans les graphes les surfaces et les noeuds, c'est-à-dire que Lacan, il fait 183 du Descartes de la géométrie algébrique mais l’algèbre qu’il emploie c’est l’algèbre de Boole, 184 c’est ce qu’à pas compris, c’est ce qu’à pas capté Badiou dans son article dans Conditions 185 quand il veut corriger Lacan, | ||||||||||||||||||||||||||||||||||||||||||||||
Dimension↑ |
✔ |
- La dimension est l'invariant topologique principal. La dimension d'un objet topologique est définie par la dimension des coupures qui le disjoingnent en plusieurs morceaux. Une dimension est faite de dimensions plus petites, elles même faites de dimensions. Etoffe p 13, 14, Il existe d'autres définitions de la dimension (dimension inductive étroit ou large, dimension par recouvrement, dimension par enroulement faite de dimensions intermédiaires, Etoffe p 15 Lacan use d'abord du terme de Catégorie pour parler du Réel, de l'Imaginaire et du Symbolique, R pour la réalité psychique, puis S et I , trois zones distinctes de son schéma R, .swf, - du point à la ligne, D1, D2, D3, ... |
||||||||||||||||||||||||||||||||||||||||||||
Etendue |
Pour la philosophie classique, l'étendue est une des propriétés de la matière, celle qu'elle a d'occuper une place dans l'espace. Descartes en fait même l'essence de la matière, comme il fait de la pensée l'essence de l'âme. L'idée d'étendue nous vient par l'exercice de l'organe du tact, après que la main, par exemple, a été l'intermédiaire de perceptions successives sur un corps. (Les paragraphes qui suivent devraient être profondément amendés à la lumière des concepts élaborés par la physique quantique et par la refonte de ceux d'espace et de temps opérée par Einstein. Nous nous en tiendrons ici aux notions auxquelles ont puisé les philosophes, c'est-à-dire celles dont la sédimention est allée de pair avec l'élaboration de la physique classique). 1° une continuité; 2° une certaine combinaison de directions du mouvement qu'elle nécessite pour être sentie. ... les lois d'après lesquelles nous explorons les dimensions des corps ne sont pas des lois de l'esprit, mais des lois de notre corps, des lois corporelles et réelles par cela même. Nous n'imposons aux autres corps les trois dimensions que parce que nous sommes nous-mêmes des corps. Si maintenant nous faisons abstraction du corps particulier qui possède les dimensions, pour ne considérer que la figure de ces dimensions, nous aurons l'étendue abstraite qui est l'objet de la géométrie. La considération isolée d'une des trois dimensions fournira l'objet de la géométrie linéaire; la considération isolée de deux des trois dimensions donnera lieu à la géométrie plane, et la géométrie dans l'espace enfin sera constituée par la considération des trois dimensions réunies. Les mathématiciens peuvent faire une géométrie à plus de trois dimensions, qu'ils ont appelée à n dimensions. Ces mathématiciens peuvent conduire très loin la série analytique de leurs déductions sans aboutir à aucune absurdité, ce qui semble bien prouver que nos conceptions géométriques à trois dimensions nous sont dictées par les relations corporelles, et que l'esprit ne fait sur ce point qu'accepter les données des sens. |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
Discret↑ |
✔ | - Discret ou discontinu..../ ≠ au continu | ||||||||||||||||||||||||||||||||||||||||||||
Discontinu↑ |
✔ |
- et la bande de moebius si je la mets en bleu, le bord ici, ( les deux parties inférieures des schémas) si je recolle ces deux bords, je vais obtenir, voyez cette portion de bord ici, et cette portion de bord là, ( V01-28.08) qui viennent se coller ensemble et qui vont donner une bande de moebius, il est évident qu’il n’est pas question de dire qu’il n’y a pas une discontinuité ! Mais justement le fait de reconnaître qu’il y ait une discontinuité, n’empêche pas de dire qu’il y a une relation entre le tore et la bande de moebius, et que cette relation n’est pas une relation d’identité topologique, puisque c’est discontinu, et que les variétés topologiques qui sont identiques elles sont nécessairement identiques selon des mouvements continus, donc ça doit plutôt nous mobiliser, il faut bien reconnaître que c’est un usage qui est judicieux, pertinent, mais pas systématique, dans la topologie, ce segment vient s’identifier avec celui là, il va venir là, et je vous le dessine comme ça, vous allez obtenir de cette manière là tout le long de la coupure vous allez obtenir cette chose là, vous allez pouvoir coller votre tore de cette manière là, (schéma inférieur gauche) le long du trait bleu qui est double, qui est comme ça, avec la partie rouge qui va venir ici se coller avec la partie verte, qui est là, et si vous continuez le coloriage, vous voyez que tout ça peut être parfaitement cohérent, puisque la partie verte, au moment où vous allez passé le bord, ce bord c’est un reste du bord périphérique du tore, et vous allez obtenir ici, la partie rouge, dessinée là, donc en coupant le tore le long de ce huit intérieur, vous n’obtenez pas ça, ( la figure inférieure gauche), vous obtenez ceci ( la figure gauche ), 36.41, V01-30.26, une bande que Lacan appelle bipartite, qui est comme ceci, entre les deux vous avez la couleur bleue qui apparaît là, parce que ici, c’est le vert de la coupure, et vous avez cette bande ici comme ceci, comme cela, là c’est un trait bleu, vous avez donc quelque chose qui est rouge ici, et vert là, et ça c’est obtenu de la coupure du tore, c’est obtenu aussi de la coupure de ce trait bleu là, ( sur la figure gauche inférieure, le trait bleu continu en cercle), et vous voyez que ça permet de contrôler quoi, que dans ces deux plis et dans ce pli, vous avez là le passage de la couleur rouge à la couleur verte intérieure, p9 JMV16062015 |
||||||||||||||||||||||||||||||||||||||||||||
Discours↑ |
✔ |
- les autres discours, voir lettre D, gaogoa - de 4 ou 5 discours, les places, |
||||||||||||||||||||||||||||||||||||||||||||
| Discours de la Science et du Kapital (DSK) (prolonge le DM)↑ |
✔ |
- DSK, le discours de la science et du Kapital, sur gaogoa, - Le discours de la science, c'est le chercheur ! qui ne trouve jamais rien et vit du l'exploitation des découvertes des autres. - C'est un discours sur la pantalon sans ôter le pantalon ! (voir Marx) - Le DSK prend le relais du Discours du Maître - Il y a une communion entre le DM, la Science, la dictature du prolétariat et dictature de l'inconscient, qui profère : pense pas, tais toi et bosse ! - mise au rencart du sexe, - Destruction du semblant, - Transformer le travail en marchandise, - Le sujet du capitalisme c'est le sujet de la science, - Le sujet d'analyse c'est le sujet de la science, il bosse et paie ...! - Le travailleur idéal c'est le sujet de la science. - Le travailleur idéal c'est la salarié esclave et spolié, le "c.." employé... |
||||||||||||||||||||||||||||||||||||||||||||
| Discret | - discret s'oppose à continu. | |||||||||||||||||||||||||||||||||||||||||||||
Droite infinie, la ↑ |
✔ |
- La seule adjonction d'une droite infinie au faux-trou fait de celui-ci un trou qui borroméennement subsite. Lacan, STH18111975, 4442-4442, - Le DI, la droite infinie, 2006, J-M.V- L'involution - Psychanalyse et mathématique, Freud contemporain de Cantor, JMV, 2007 : - |
||||||||||||||||||||||||||||||||||||||||||||
Dualité↑ |
✔ |
- Dualité logique, dualité de De Morgan, in -Le vel de l'aliénation, 2006, JMV - échange des pleins et des vides dans une présentation donnée. Noeuds p56 - Dualité en topologie : le nœud ou la chaîne modifient l'espace dans lequel ils sont plongés. -Dualités pour le noeud de Lacan, .swf, |
||||||||||||||||||||||||||||||||||||||||||||
| Dualité | ✔ |
- Une dualité est définie à l'intérieur d'une famille F d'objets mathématiques, c'est-à-dire qu'à tout objet X de F on associe un autre objet Y de F. On dit que Y est le dual de X et que X est le primalde Y. Si X = Y (par = on peut sous-entendre des relations d'isomorphies complexes), on dit que X est autodual.
Dans de nombreux cas de dualité, le dual du dual est le primal. Ainsi, par exemple, le concept de complémentaire d'un ensemble pourrait être vu comme le premier des concepts de dualité. Utilisations : |
W, |
|||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
| E | ||||||||||||||||||||||||||||||||||||||||||||||
| Echeveau | - voir Entrelacs, Noeuds, Tresses, Chaines, Echeveau, sur gaogoa, | |||||||||||||||||||||||||||||||||||||||||||||
Ecriture
|
✔ |
- La vérité parle, le savoir écrit ! - que la parole c'est continue et que ça dit la vérité, alors que l'écriture est discrète et produit du savoir, c'est à cette occasion là qu'on parle du savoir, qui n'est pas la connaissance, ce n'est pas non plus un savoir faire, c'est un savoir lire, savoir écrire, savoir compter, le savoir ça commence avec la différence entre l'écrit et la parole, JMV09092014, - Le corps écrit, déviant ses organes pour faire des lettres, il est entré dans cette fonction par les oreilles, aussi, "ça parle" ! in "ça claque", p60, JMV - L'écriture permet de se corriger, - Les animaux parlent mais n'écrivent pas ! Le corps écrit, déviant ses organes pour en faire des lettres (pas uniquement alphabétique !!), et il est entré dans cette fonction, comme sujet du langage, par les oreilles, d'où que "ça parle". Pas de déviation sexuelle, car le sexe, soit le langage de ce mammifère n'est que déviation. L'écriture va jusqu'à la castration de l'Autre, son manque. - Psychanalyse et mathématique, Freud contemporain de Cantor, JMV, 2007, de l'écriture - l'écriture est un délire alphabétique qu va donner un certain nombre de textes religieux, à partir des alphabets , mais ça a été calqué sur la numération par position, ( JMV09092014, 00.30) .., des arabes et des indiens, nous héritons de leurs chiffres, c'est-à-dire des lettres qui écrivent les nombres, et du coup on croit que ça va donner une écriture, l'écriture alphabétique c'est un délire ! La voix c'est un processus continue , et le propre de l'écriture c'est justement de découper, la lecture et l'écriture c'est de la découpe , et vous avez ça dès les premières pages de Freud, 0.32.44, et vous avez ça dès les premières pages de Freud sur les Aphasies - on fabrique des Lettres et des Noms propres avec des restes de discours tombés en désuétude - Du fait du Symbolique, il y a des peuples qui inventent une écriture. (cas du chinois à partir des écailles de tortue ! ... à partir de déchets ...) - de la polyvalence structurale littérale (JMV09062015) - Lecture puis écriture ... - L’écriture Introduit la discontinuité dans le continu, hors il se trouve que ça fonctionne très bien avec le phonème, qui est d’abord parlé, ce que Lacan appelle le Signifiant, et moi je vous propose de parler du phonème dans la psychanalyse avec Lacan en terme de Signifiant pour ce qui est du côté des oreilles, dans ce qui s’entend, et de parler du phonème dans ce qui s’écrit et qui s’appelle la Lettre chez Lacan, vous avez ça dans l’Instance de la lettre, Lacan parle, au moment ou Lacan introduit l’algorithme Saussurien, le S/s, il parle de la chaine signifiante et il dit, et il parle de l’élément différentiel dernier qui est la Lettre et qu’on appelle phonème, !!, alors voyez là, il emploie le mot phonème pour la lettre ! et même le mot phonème pour le lettre et le mot lettre pour le phonème, donc moi je pense que le phonème des linguistes, il y a le phonème dans la langue parlée, du locuteur, dans la langue vulgaire, dans la langue de celui qui parle de manière plus ou moins continue, dans le flux verbal qu’on ne comprend pas si on ne le découpe soit même, donc écouter quelqu’un ou lire, c’est découper, c’est introduire ce que Freud appelait dès les Etudes sur l’aphasie, les verneinugzeichen, voyez dans les schémas de Freud, vous avez Verneinung et Verneinungzeichen, vous avez perception et perception-signe, JMV16062015, - vous avez cette idée que les chinois eux n’ont pas cherchés à faire une géométrie ils ont cherchés à construire un discours divinatoire pour prédire l’avenir, mais que ça a donné des traits distinctifs, des lettres, on va appeler ça des lettres, qui ne font pas partie d’un alphabet, et c’est donc, et il n’est pas exclu que l’’écriture silencieuse vienne avant l’écriture de la langue, et que l’écriture de la langue vienne forcément d’abord avant l’écriture mathématique, ça veut dire qu’il ne faut pas se précipiter de conclure. JMV23062015, |
||||||||||||||||||||||||||||||||||||||||||||
Effacement
|
✔ |
- Les principes de la pensées, in l'Amour du tout, JM-Vappereau - oubli, mémoire, ardoise magique, inscription, trace, généralisation, - Freud invente la cure analytique un procédé pour retourner dans cet autre lieu, qu’il appelle l’Autre scène, l’Inconscient, ce, sans dormir ! Pourquoi il y a de l’inconscient et bien parce que il y a des sujets qui veulent raconter leurs rêves, et ces rêves sont des messages, des textes qui viennent de cette Autre scène, qui est structurée par une autre logique, par une autre syntaxe, donc il faut étudier pour chacun la pratique, c’est pas un savoir, moi je ne fais pas des analogies avec ça, je prétends pas du tout, et je dis que dans l’écriture, ça ( en désignant les diagrammes de 3 ronds au tableau) , étudier la Logique modifiée à côté de la Logique classique c’est formateur, ça me permet à moi, d’être épaté par le fait que ça s’efface, .. Alors j’ai fait deux expériences d’effacement majeures, V02-50.38 ; c’est deux textes qui sont dans ma page, qui s’appellent L’Amour du tout aujourd’hui, (argument II) j’ai écrit la Loi de la Vérité de Tarski, (argument IV) en Logique modifiée, et le fait de l’écrire l’efface ! V02-50.51 ; JMV20150602 , - le Sujet c’est comme un prestidigitateur qui joue avec une pile d’assiette dans les mains et qui veut faire un tour, et qui rate son tour, alors toutes les assiettes se cassent la gueule et il reste avec deux morceaux d’assiettes dans les mains, c’est une chose qui arrive constamment, c’est l’effacement de la logique modifiée, JMV20150602, |
||||||||||||||||||||||||||||||||||||||||||||
effectivité
|
✔ |
- c'est l'enchainement (JMV020914-39.42) - voir Chaine, lettres et noeuds, |
||||||||||||||||||||||||||||||||||||||||||||
| Eléménts de géométrie d'EUCLIDE, Les | ✔ |
- Les éléments de géométrie d'EUCLIDE, , source remacle, - Géométries, gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
| Eléments de mathématique, BOURBAKI.N | ✔ |
BOURBAKI, Elements de mathématique, et sur W, | archives-bourbaki | ↑, |
||||||||||||||||||||||||||||||||||||||||||
3.1 Première partie 3.1.1 Théorie des ensembles (1939-1970) |
||||||||||||||||||||||||||||||||||||||||||||||
3.2 Deuxième partie (depuis 1960) 3.2.1 Groupes et algèbres de Lie (1960-1982) 3.3 Éléments d'histoire des mathématiques (1960-1974) |
||||||||||||||||||||||||||||||||||||||||||||||
| Empan | ✔ |
- Surface d'engendrement du noeud. - voir Surface d'empan |
||||||||||||||||||||||||||||||||||||||||||||
Enlacement ↑
|
✔ |
- folie névrotique de l'enlacement, Noeud p 300, - Le plus petit non-nœud est une chaine de deux ronds, dont un fils emprunte le trou de l'autre et réciproquement.Noeud p35 |
||||||||||||||||||||||||||||||||||||||||||||
énonciation |
✔ |
- « la neige est blanche » est vrai , c’est un segment cité comme le dit Tarski dans son exposé, il le met entre guillemets, c’est donc une citation, pourquoi ? parce que ça vient à la place du sujet d’un prédicat : est vrai, donc « la neige est blanche » est vrai, c’est « la neige est blanche » c’est cité, c’est la mention, dit Tarski, la mention de « la neige est blanche » dire que c’est vrai, il met des guillemets et c’est là, c’est là-dessus que s’applique la fonction de vérité, si et seulement si la neige est blanche, mais là il faut considérer que la seconde occurrence de la neige est blanche, dans cette seconde occurrence, il ne s’agit pas du fait physique de la couleur de la neige, il s’agit de l’énonciation, si quelqu’un dit « la neige est blanche », c’est vrai, c’est ça l’énonciation ! et ça c’est la fonction de l’autorité de la parole, et de la fonction phallique, qui est la fonction de ce type d’autorité, qu’il ne faut pas rabattre trop vite sur les parties génitales, et imaginaires du corps, ...JMV16062015 - voir Noeud, Parole, |
||||||||||||||||||||||||||||||||||||||||||||
Entrelac Entrelacs ↑ |
✔ |
- voir Entrelacs, Noeuds, Tresses, Chaines, Echeveau, sur gaogoa, - en Théorie des noeuds, wiki, - def wiki , - Entrelacs et graphes, wiki, - Cours de dessins d'entelacs.... |
||||||||||||||||||||||||||||||||||||||||||||
Entrelac brunien ↑ |
✔ |
- voir Borroméen ou noeud borroméen, - Brunien, de Hermann Brunn, l'entrelac brunien le plus simple est le noeud borroméen.(Jablan.S.V) |
||||||||||||||||||||||||||||||||||||||||||||
Entrelacs de Hopf ↑ |
✔ |
- entrelacs de Hopf, wiki, | ||||||||||||||||||||||||||||||||||||||||||||
Enseignement↑ |
✔ |
- L'enseignement n'est pas la transmission d'un savoir, c'est pas les vases communiquants. On enseigne pour s'instruire, s'instruire de ses erreurs et les corriger. Chacun ne peut apprendre qu'à la mesure de son savoir. Ce savoir acquis au temps du trauma forme l'intuition du sujet, qui passera sa vie à trouver les bonnes formules de ce qui s'écrit symptomatiquement sur la table de jeux de son corps et de ses pensées. Sujet qui préférera le plus souvent masquer ou dissimuler les rattages de ses essais... ( ne cherchons pas plus loin pour objectiver le propos que le flacon de Tipp-Ex de votre bureau, sans parler de la touche retour de votre clavier .. et des miens ..!.) - le mot d’esprit, et c’est la seule transmission raisonnée, et raisonnable, parce que le sujet malgré même le jugement qu’il va avoir, il va rire, donc il faut une métaphore, c’est par les incorporelles, il faut un mot d’esprit, il faut quelque chose que ce soit savant, érudit ou vulgaire, pour moi le prototype de la lisibilité, c’est le fait qu’un type, on lui raconte une histoire, et il rit, ensuite il va le répéter, c’est la seule transmission profane, et tout ces espèce de curés qui nous parlent du Père, du Nom de baptême, parce qu’il y a les Nom du père, le nom de baptême dans Kripke, c’est le sobriquet, il dit que les logiciens l’appelle Nom de baptême, pourquoi cette référence religieuse, vous voyez bien que le sobriquet c’est un mot d’esprit, vous parlez de quelqu’un dans un groupe, que tout le monde connait, et vous l’appelez Lunette ou Moustache, si le mot est bien trouvé tout le monde pige, tout le monde rigole, et dit que c’est pas mal trouvé, c’est ça le mot d’esprit, et c’est la seule transmission raisonnée, et raisonnable, parce que le sujet malgré même le jugement qu’il va avoir, il va rire, et quand un mot l’a faire rire, il va avoir du mal de s’empêcher d’aller le raconter à quelqu’un ! Mais il y a des sujets qui ne comprennent pas les mots d’esprits ! JMV20150602 - voir Inititiation, -Parcours mathématique de Lacan, -Mathématiques et Séminaires, -Il y a trois chapitres topologiques dans l'enseignement de Lacan, rapportés à trois types de variétés mathématiques : graphes (1953-1961), surfaces (1961-1971), noeuds (1972-1981) - Psychanalyse et mathématique, Freud contemporain de Cantor, JMV, 2007, Matemata, Mathème - Idéal des facultés à développer ... - Scilicet : tu PEUX savoir, et non : tu dois savoir ! Le sujet est convoqué ....à y mettre du sien ! (et du chien !). |
||||||||||||||||||||||||||||||||||||||||||||
Ensemble↑ |
✔ |
- Voir Théories des ensembles, ci-dessous,
|
||||||||||||||||||||||||||||||||||||||||||||
| Ensemble cantorien, | ✔ | - définition d'un ensemble cantorien, JMV27012015, et ici, | ||||||||||||||||||||||||||||||||||||||||||||
Ensemble infini
|
✔ |
- En mathématiques, plus précisément en théorie des ensembles, un ensemble infini est un ensemble qui n'est pas fini, c'est-à-dire qu'il n'y a aucun moyen de « compter » les éléments de cet ensemble à l'aide d'un ensemble borné d'entiers. Un ensemble en bijection avec un ensemble infini est donc infini. Tout ensemble contenant un ensemble dénombrable est infini. W, - un ensemble est infini s'il est une bijection avec un de ses vrais sous-ensemble. - C'est une collection d'objets, de nombres, comptant une infinité de ces objets. L'ensemble de nombres entiers est infini: il contient une collection sans fin de nombres: {0, 1, 2, … 123, 124, …}. Les trois points indiquent qu'il n'y a pas de limite à la succession de ces éléments. Le symbole L'ensemble des nombres entiers positifs est décrit par: {tous les nombres de zéro à l'infini}. |
||||||||||||||||||||||||||||||||||||||||||||
Ensemble vide |
✔ |
- L'ensemble vide peut être noté d'un O barré, à savoir Ø ou simplement { }, qui est une paire d'accolades ne contenant qu'une espace, pour représenter un ensemble qui ne contient rien. La notation Ø a été introduite par André Weil, dans le cadre de l'institution de notations par le groupe Bourbaki. - Lacan dit que le Symbolique tient au corps par les incorporels, et ensuite il embraye sur les étoiles dans le ciel, et les sépultures, il va jusqu’à dire un truc incroyable, il va jusqu’à dire que dans la sépulture, les ossements qui sont réunis là, au milieu des autres objets de la jouissance, qui sont les attributs de la jouissance, les ossements c’est l’ensemble vide de la théorie des ensembles de Cantor, ça montre jusqu’où Lacan porte sa lecture, JMV16062015, |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Entier naturel
|
✔ |
- Classification des nombres, - Nombre entier positif ou nul, (nombres) |
||||||||||||||||||||||||||||||||||||||||||||
Enveloppement↑ |
✔ |
- Le collier fait d'anneau d'une chaîne peut être enveloppé dans un tore. (Conséquence de la définition de la chaîne signifiante de Lacan les 14-26 mai 1957 !!! : la chaine signifiante : anneaux dont le collier se scelle sur l'anneau d'un autre collier fait d'anneaux) . L'instance de la lettre dans l'Inconscient, ELP, date du 1957-05-09, |
||||||||||||||||||||||||||||||||||||||||||||
Equation diophantienne |
✔ |
- Equation dont les coefficients sont des nombres entiers et les solutions recherchées sont également entières. Terme utilisé aussi pour les équations à coefficients rationnels. Elles participent d'une branche des mathématiques nommée : Arithmétique. ax +by = c |
||||||||||||||||||||||||||||||||||||||||||||
| -Une équation diophantienne, en mathématiques, est une équation polynomiale à une ou plusieurs inconnues dont les solutions sont cherchées parmi les nombres entiers, éventuellement rationnels, les coefficients étant eux-mêmes également entiers. La branche des mathématiques qui s'intéresse à la résolution de telles équations s'est appelée longtemps l'analyse indéterminée avant de se fondre dans l'arithmétique ou la théorie des nombres.
Si l'expression du problème posé est parfois simple, les méthodes de résolution peuvent devenir complexes. Carl Friedrich Gauss, au XIXe siècle, écrivait de la théorie des nombres que « son charme particulier vient de la simplicité des énoncés jointe à la difficulté des preuves. » exemple : Gauss se plaignait « des efforts démesurés que lui a coûté la détermination d'un signe d'un radical dans la théorie des nombres ; bien d'autres choses ne l'ont pas retenu autant de jours que cette question l'a retenu d'années. » Le dernier théorème de Fermat est un exemple archétypal ; il est conjecturé par Pierre de Fermat et démontré en 1994 par Andrew Wiles, après 357 ans d'efforts de la part de nombreux mathématiciens. |
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
Equipotence
|
✔ |
- Deux ensembles sont équipotents s'il existe une bijection de l'un sur l'autre ( "équivalents" pour Cantor) | ||||||||||||||||||||||||||||||||||||||||||||
En mathématiques, l’équipotence est une relation entre ensembles, selon laquelle deux ensembles sont équivalents lorsqu'il existe une bijection entre eux. Cette notion permet de définir la cardinalité, c'est-à-dire le nombre d'éléments d'un ensemble, qu'il soit fini ou infini. La subpotence est une relation plus faible, satisfaite lorsqu'il existe une injection entre deux ensembles. Elle permet de définir une comparaison de taille entre les ensembles, sans présupposer la construction des nombres cardinaux. |
W, |
|||||||||||||||||||||||||||||||||||||||||||||
| Enchevêtrement, | « Ce livre traite des enchevêtrements. Être enchevêtré n’est pas seulement être entrelacé avec un autre, comme dans l’assemblage d’entités séparées, c’est être privé d’existence indépendante, autonome. L’existence n’est pas une affaire individuelle. Les individualités ne préexistent pas à leurs interactions ; les individualités émergent plutôt de leur intra-relation enchevêtrée et dépendent d’elle. Ce qui ne veut pas dire que l’émergence se produit une fois pour toutes, comme un évènement ou un processus qui s’effectue conformément à une mesure extérieure de l’espace et du temps, mais plutôt que le temps et l’espace, comme la matière et la signification, viennent à l’existence, sont reconfigurés itérativement à chaque intra-action, rendant ainsi impossible de différencier formellement création et recommencement, origine et retour, continuité et discontinuité, ici et là, passé et futur ». Karen Barad |
|||||||||||||||||||||||||||||||||||||||||||||
| Erlangen, Programme d'..., | - Le programme d'Erlangen, Felix KLEIN, 1991, Editions GABAY, Table des matières, et gaogoa - Wikipedia, Wikiversity, Hist-Math, B.YCART, SABIX : Genèse du ...par RUSSO.F, GABAY, Ed, - Textes (I, II) mathématiques de F.KLEIN, gaogoa, - Klein et Lie, gaogoa, & Mathématiques sur gaogoa, |
|||||||||||||||||||||||||||||||||||||||||||||
Le programme d'Erlangen (1872) : Comme Descartes l’avait fait avec l’algèbre de son temps, l’Allemand Christian Felix Klein et le Norvégien Sophus Lie utilisent celle du XIXe siècle pour étudier la géométrie. Klein donne ainsi une classification des géométries en fonction de leurs groupes de transformations (programme d’Erlangen). Lie procède à une étude géométrique des équations différentielles, au moyen de groupes continus de transformation appelés groupes de Lie. Au XXe siècle, l’algèbre s’applique également à une autre approche de la géométrie appelée topologie. Au XIXe siècle, les fondements des mathématiques sont bouleversés, en particulier par l’ouvrage de George Boole, Recherches sur les lois de la pensée (1854), et par la théorie des ensembles de Cantor. Cependant, vers la fin du XIXe siècle, on découvre une série de paradoxes dans la théorie de Cantor. Bertrand Russell met en évidence un paradoxe à propos de la notion d’ensemble. Les mathématiciens reformulent alors des théories des ensembles suffisamment restrictives pour éliminer ces paradoxes, mais la question reste ouverte de savoir si d’autres paradoxes ne surgiront pas de ces théories, c’est-à-dire de savoir si ces théories sont consistantes. Depuis, et jusqu’à ce jour, on n’a pu donner que des démonstrations de consistance relative, c’est-à-dire correspondant au schéma suivant : la théorie A est vérifiée si la théorie B l’est. Un résultat particulièrement troublant est démontré en 1931 par Kurt Gödel : dans tout système d’axiomes, il est possible de construire des propositions qui ne peuvent être démontrées. |
||||||||||||||||||||||||||||||||||||||||||||||
| Espace topologique | ✔ | - De la même manière qu'en algèbre générale, les notions de groupes, d'anneaux et de corps généralisent ce que nous savons de l'addition des réels à des structures plus abstraites, voire exotiques, la structure d'espace topologique permet de généraliser celle d'espace euclidien à des objets mathématiques de nature totalement différente (espace de nombres, espaces fonctionnels…). L'intuition géométrique joue un grand rôle en topologie, bien qu’il faille toujours se méfier des dessins (dont la pertinence est limitée quand il s'agit de représenter des espaces de dimension infinie).
On définit donc la structure de base de la topologie : l'espace topologique, défini comme la donnée d’un ensemble X et d’une topologie sur X , c'est-à-dire un ensemble de sous-ensembles de X vérifiant certaines propriétés, dont les éléments sont appelés ouverts. Intuitivement, un ouvert correspond à un ensemble qui ne contient pas sa « frontière ». |
|
|||||||||||||||||||||||||||||||||||||||||||
Un espace topologique est un couple ( X , T ), où T est un ensemble de parties de X , vérifiant les trois propriétés :
T s’appelle une topologie sur l'ensemble X . La plupart du temps, la topologie est sous-entendue, si bien qu'on commettra l'abus de parler de « l'espace topologique X » (au lieu de ( X , T ) ). Les éléments de T sont appelés les ouverts de cet espace. - Voir Topologie Générale, ci-dessous, |
||||||||||||||||||||||||||||||||||||||||||||||
Essaim |
✔ |
- le livre Essaim, TEE, de Jean-Michel-Vappereau |
||||||||||||||||||||||||||||||||||||||||||||
| Esthétique | ✔ |
- voir Esthétique, | ||||||||||||||||||||||||||||||||||||||||||||
| Ethique | ✔ |
SOCRATE, PLATON, ARISTOTE, ZENON,EPICURE, BIBLE, DESCARTES, KANT, HEIDEGGER, LEVINAS, - W, L'éthique est une discipline philosophique portant sur les jugements moraux et dont le concept est donc très proche de celui de la morale. C'est une réflexion fondamentalede tout peuple afin d'établir ses normes, ses limites et ses devoirs. Dans les pays laïcs, l'éthique est étroitement liée à la philosophie politique qui la sous tend, mais elle peut aussi être liée à la culture, la religion, les croyances et les traditions d'un pays, d'un groupe social, ou d'un système idéologique. Pour des philosophes tel qu'Aristote ou Kant, l'éthique a pour but de définir ce qui doit être. - L'Éthique ou la Morale démontrée par la méthode géométrique (Ethica ordine geometrico demonstrata) est un traité philosophique de SPINOZA, L'ouvrage est divisé en cinq parties : la première traite de Dieu, la seconde de la nature et de l'origine de l'âme, la troisième de la nature et de l'origine des passions, la quatrième de la servitude humaine, et la cinquième de la liberté humaine ou de la puissance de l'intelligence. Une substance unique; deux attributs, la pensée et l'étendue; les modes divins de ces deux attributs formant toutes les existences indépendantes; la source unique de l'étendue et de la pensée inconnue en elle-même et dépouillée d'un entendement déterminé et d'une volonté personnelle; l'âme humaine considérée comme une collection d'idées, le corps humain comme une collection de propriétés, la liberté comme une illusion de la conscience le vice comme une simple privation (defectus) : voilà en quelques mots la doctrine de Spinoza. in cosmovisios, - Séminaire VII, l'Ethique de la psychanalyse, LACAN, |
||||||||||||||||||||||||||||||||||||||||||||
Etoffe↑ |
✔ |
- Lacan distingue deux modalités de l'étoffe à la fin de son premier chapître topologique, Ep793-827 : Il y a le fantasme, S <> a (S barré poinçon a) , étoffe du sujet de l'insconscient, où S barré signe le refoulement originiare, Ep816, L'acte d'énonciation du sujet renverse instantanément le schema R en schéma L et le fantasme fait alors étoffe de la fermeture de la caverne condensé dans le poinçon . La structure de la surface est unilatère. Et il y a l'objet a, constante au sens mathématique, et objet au sens de la théorie des ensembles . L'objet a est l'étoffe du sujet, composition entre Perception et Conscience, détourné par la dérive de l'Inconscient, et tendu entre l'objet de la phobie (névrose) et le fétiche (perversion). Cet objet relève d'une structure de surface bilatère. d'après Etoffe p 25 |
||||||||||||||||||||||||||||||||||||||||||||
| Evanouissement ↑ | voir Théorie de l'évanouissement | |||||||||||||||||||||||||||||||||||||||||||||
Eulérien↑ |
✔ |
- Un chemin est eulérien en tant que l'on ne passe qu'une fois et une seule fois par chaque arête. - En théorie des graphes, un parcours eulérien ou chemin eulérien1, ou encore chaine eulérienne d'un graphe non orienté est un chemin qui passe par toutes les arêtes, une fois par arête. Le nom a été donné en référence à Leonhard Euler. Si un tel chemin revient au sommet de départ, on parle de circuit eulérien3 ou cycle eulérien, ou encore tournée eulérienne. Un graphe qui admet un circuit eulérien est dit eulérien. S'il admet un parcours eulérien, il est dit semi-eulérien. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Euler-Venn |
✔ |
- Diagramme d'Euler-Venn, JMV20150602, p4 - Diagrammes d'Euler, de Venn et de Caroll, : des schémas géométriques utilisés pour représenter des relations logico-mathématiques. Créés pour visualiser la structure logique des syllogismes, ils sont couramment utilisés pour l'étude des relations entre ensembles. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Extérieur↑ |
✔ |
-
Qui se trouve le plus éloigné du milieu, du centre réel ou fictif.CNRTL L'algèbre extérieure est utilisée en mathématiques dans la théorie des déterminants qui permettent de calculer les volumes et les surfaces. L'algèbre extérieure permet en particulier de définir les formes différentielles sur une variété et les champs de multivecteurs. Les formes différentielles sont particulièrement utiles en topologie algébrique et surtout en géométrie différentielle et en physique mathématique. En géométrie algébrique, l'algèbre extérieure intervient dans l'étude des faisceaux localement libres. Ces applications sont à peine abordées dans cet article qui se veut avant tout introductif. |
||||||||||||||||||||||||||||||||||||||||||||
Extrinsèque↑ |
✔ |
- Qui est extérieur à l'objet que l'on considère; qui ne lui appartient pas mais dépend des circonstances, de faits accessoires. CNRTL - Afin de préciser le narcissisme, JMV, 2007, Intrinsèque extrinsèque, la géométrie, la symétrie, la symétrie miroir, L'envers du narcissisme - Deux aspects géométriques du narcissisme, JMV 17 mai 2011 |
||||||||||||||||||||||||||||||||||||||||||||
| Les propriétés intrinsèques et extrinsèques d'un système ou d'une entité sont la distinction de leurs caractéristiques et fonctionnement selon leur degré de dépendance de facteurs externes : dépendance nulle ou voisine de zéro dans le cas d'une propriété intrinsèque entièrement définie par la constitution ou nature de l'objet considéré. Une propriété intrinsèque est ainsi indépendante de la quantité de matière présente autant que de sa forme, par exemple, un grand fragment ou une collection de petites particules. Les propriétés intrinsèques dépendent principalement de la composition chimique ou de la structure de la matière | W, |
|||||||||||||||||||||||||||||||||||||||||||||
| F | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
Famille Groupe |
✔ |
- La famille reste un sinthome dans le symptôme psychanalytique (arg III, p172, clef pour la passe) - Les complexes familiaux, 1938, Lacan, - Le territoire de la phobie, 2008, JMV, - Le bavardage sur la famille est une rente, en user jusqu'à la trame en assure le rendement. Le ver est dans le fruit et " Les pères ont mangé des raisins verts et les dents des enfants en ont été agacées ". Ezéchiel chap 18 verset 1 à 9. C'est le lit des nourrices ...! Vite, passer son chemin ! - La famille est le Royaume des Chaînes ... heureusement il y a des fins de séries ....! - Se référer aux Groupes, aux Foules, voir Freud... (Psychologie des foules et analyse du Moi), Voir théorie des groupes .... |
||||||||||||||||||||||||||||||||||||||||||||
Famille des Lacan (noeuds de la) |
✔ |
- Les nœuds propres dit de Lacan, dont le Lacan, 3322-442, est un prototype, sont des « non-nœuds », c'est-à-dire qu'ils sont bilatères, et ne nécessitent donc pas de coupure !Np68 |
||||||||||||||||||||||||||||||||||||||||||||
Fonction |
- Une fonction est une mise en correspondance d'un ensemble avec un autre ( en général R) . - Lorsque des quantités variables sont tellement liées entre elles, que, la valeur de l'une d'elles étant donnée, on puisse en conclure les valeurs de toutes les autres, on conçoit d'ordinaire ces diverses quantités exprimées au moyen de l'une d'entre elles, qui prend le nom de variable indépendante; et les autres quantités, exprimées au moyen de la variable indépendante, sont ce qu'on appelle des fonctions de cette variable. |
|||||||||||||||||||||||||||||||||||||||||||||
Fantasme ↑ |
✔ |
- Un fantasme est une phrase du modèle "Un enfant est battu." La sublimation égalise et complète les sommets formés par la répétition et la hâte articulés dans un temps logique, ce dans un nouveau graphe de Klein. et inscrive la distance du Sujet supposé savoir dans son insertion au Réel, satisfaisant à la logique ici proposée, car il n'y a pas d'autre entrées pour le sujet dans le réel que le fantasme ! Le fantasme a fonction d'axiome, et figure dans chaque structure, dans chaque symptôme, comme constante. Lien à la théorie des ensembles. Le fantasme rendu au clavier de la logique en fera percevoir la place qu'il tient pour le sujet (AE323) - Lacan distingue deux modalités de l'étoffe à la fin de son premier chapître topologique, Ep793-827 : Il y a le fantasme, - Topologie ( E-V) de la logique du fantasme, JMV 2014, |
||||||||||||||||||||||||||||||||||||||||||||
Faux↑ |
✔ |
- voir Vérité, vrai, - voir Vérifonctionalité, |
||||||||||||||||||||||||||||||||||||||||||||
Faux-trou↑ |
✔ |
- Faux-trou, - Le faux-trou, qui est un mode de nouage de deux anneaux ou colliers, diffère de l'enlacement car elle permet que se développe l'essaim signifiant. P132 |
||||||||||||||||||||||||||||||||||||||||||||
Fibonacci, suite de ↑ |
✔ |
- R suites, F suites, suite des rapports..; -En mathématiques, la suite de Fibonacci est une suite d'entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent. Elle commence par les termes 0 et 1 si on part de l'indice 0, ou par 1 et 1 si on part de l'indice 1. Notée ( Fn ) , elle est donc définie par F0 = 0 , F1 = 1 , et Fn = Fn − 1 + Fn − 2 pour n ≥2. Les termes de cette suite sont appelés nombres de Fibonacci et forment la suite A000045 de l'OEIS : 0, 1,1, 2, 3, 5, 8, 13, 21, 34, ... Cette suite est liée au nombre d'or, φ (phi) : ce nombre intervient dans l'expression du terme général de la suite. Inversement, la suite de Fibonacci intervient dans l'écriture des réduites de l'expression de φ en fraction continue : les quotients de deux termes consécutifs de la suite de Fibonacci sont les meilleures approximations du nombre d'or. suite sur Wikipedia, |
||||||||||||||||||||||||||||||||||||||||||||
Fichéennes (Chaînes)↑ |
✔ |
- en quoi consiste la partie prototypique des nœuds borroméens, Essaim p 131 |
||||||||||||||||||||||||||||||||||||||||||||
Folie↑ |
✔ |
- voir Folie 1) hors Table Structures freudo lacanienne du Symptôme, et 2) discours fous, ici aussi, - la folie ne se soigne pas... elle ne relève pas de la psychanalyse, elle sévit et s'évite (surtout), ou se combat ! - voir Fou |
||||||||||||||||||||||||||||||||||||||||||||
Fonction imaginaire du phallus symbolique↑ |
✔ |
- la fonction imaginaire du phallus symbolique et le parlêtre en équation, in Eros et psyché, JMV, partie 2, - Fonction imaginaire du phallus symbolique : elle ne connait que 2 constantes notées : 0 et 1 avec leurs relation d'aliénation non Réciproque (0 <≠1 ). |
||||||||||||||||||||||||||||||||||||||||||||
Fonction phallique ↑ |
✔ |
-DI (ou la Dei)=trauma=le Phallus=la Parole=fonction phallique - ou phonction phallique du F (grand phi), comme phonction phonatoire (le Sinthome 16031976) |
||||||||||||||||||||||||||||||||||||||||||||
fonction du phallus symbolique |
✔ |
- Fonction imaginaire du pallus symbolique : la fonction de l’énonciation qui à mon avis est découverte par l’enfant au moment du trauma, quand les parents justement n’en tiennent pas compte, et bien c’est la fonction phallique, mais c’est pas la fonction imaginaire du phallus des animaux, dans la sexualité animale, c’est la fonction imaginaire du phallus symbolique, qui va redevenir génitale au moment du narcissisme, dans l’image du corps, dans l’image narcissique, cette fonction d’autorité, de puissance, cette fonction phallique de la parole va redevenir génitale avec la question des éléments en pointe dans la géométrie, les éléments en pointes nécessaires à créer une différence de notre image dans le miroir, image symétrique, et puis les organes érectibles, chez le mâle, alors les enfants ne sont pas complètement crétins, ils font des théories phalliques, mais dans toute la période qui est prégénitale, avant l’Œdipe, le phallus c’était la puissance érotique, JMV20150602, .pdf, - voir Effectivité - voir Parole, |
||||||||||||||||||||||||||||||||||||||||||||
✔ |
- les tables de vérité, vous savez, elles ont été introduites en 1921, par Post, c’est Post qui a montré que la syntaxe du système d’écriture de cette logique classique des connecteurs logiques découverts par Frege, c’est découvert par Frege dans Recherche logique, et s’est développé ensuite, et comme Russel va adopter le point de vue de Frege en parlant des fonctions propositionnelles pour les concepts, Frege il était très inquiet de cette question, il a écrit 4 articles fameux, à cause de cette inquiétude qu’il avait, il se rendait bien compte que c’était un geste, un acte extrêmement important que d’appeler le concept fonction propositionnelle ! Passer de quelque chose qu’on peut appeler concept, C(x), qu’on écrit à la rigueur comme ça, lui il dit : c’est une fonction, F(x), le concept, c’était le prédicat P(x), vous trouvez ça, ça rentre lentement dans l’écriture contemporaine et occidentale, mais Frege lui va parler de fonction propositionnelle, mais les fonctions et les concepts, nous sommes là dans la notion du calcul des prédicats, donc ici vous avez le mot concept, le mot prédicat, et si vous prenez la syllogistique d’Aristote, vous voyez que dans la Syllogistique d’Aristote, vous avez un concept prédicat et vous avez un concept sujet, et tout ça ça va être des fonctions propositionnelles pour Frege, mais lui il se rend compte que c’est un acte, Russell, lui ne s’en rend pas compte, il l’adopte, c’est rendre hommage à Frege, même si Frege il est un peu raide, c’est quand même un grand logicien, il a tout à fait la notion du risque délirant voir psychotique qu’il y a à vouloir parler des fonctions propositionnelles à propos des concepts, d’ailleurs c’est ce qui fait que durant tout le XX siècle on a continué à se bagarrer en philosophie contre la logique mathématique, en disant qu’il y a avait deux logiques, il faut voir ce que raconte madame Claude Imbert, c’est complètement idiot, c’est très bien ce qu’elle dit sur l’Histoire de la logique, mais pour ce qui est de la logique de Lukasiewicz même si Lukasiewicz était très timide, très timoré, c’est un grand logicien, V01-43.52 ; son analyse et sa lecture de la syllogistique d’Aristote, qu’il a mené pendant 50 ans, c’est quelque chose de magnifique, c’était presque prêt à publier en 19o5, il l’a publié en 1955, JMV20150602 - Ecrits logiques et philosophiques, G.FREGE, Vrin, 1971, & C.IMBERT, .pdf, |
F, |
||||||||||||||||||||||||||||||||||||||||||||
fonction Ψ |
✔ |
- Ce noeud là à 6 croisements, ça commence avec celui là, (le trèfle) ceux là ce sont des nœuds non triviaux, des nœuds propres, faits d’un seul fil, à gauche c’est le nœud trivial, c’est le nœud zéro, 0, alors ici vous avez (u, V) pour les nœuds logiques, vous avez des nœuds logiques, pour n’importe quel (u, V), il faut sa placer dans une algèbre de Boole qui est plus grande, qui s’appelle Z2n = [(0,1)n , +uV, xuV] comment créer ce plongement que j’appelle psy, Ψ u,V, comment balancer la logique classique avec tout ce qui suit, et qu’on va regarder, en particulier avec le fait qu’on y trouve l’aliénation, comme étant une condition nécessaire de la logique classique, l’aliénation au sens ou Lacan la définit, et tout ce qui est ici (à gauche) doit se trouver développé là, (à droite) , mais comment on passe de l’un à l’autre par une fonction que j’appelleΨuV; V01-37.03 il y a une fonction, il y a un plongement pour chaque nœud logique, ici il y a un plongement qu’on peut appeler N, N indice x, pour chaque nœud qui va du cercle S1 à ces objets là qui sont noués, qu’on peut appeler Nx, les nœuds topologiques, il s’agit de déformations..., JMV20150602 - JMV20150602, p21, p10, p30 |
||||||||||||||||||||||||||||||||||||||||||||
| Fonction de vérité | ✔ |
- fonction identité - fonction phallique, - , là vous retrouvez la fonction identique, i(x) = x, c’est la fonction phallique, pourquoi, parce que c’est la fonction de la vérité, c’est la fonction de la parole, qu’est ce que c’est que la vérité pour Tarski, c’est : « la neige est blanche » est vrai, si et seulement si la neige est blanche, (x) « la neige est blanche » est vrai, i, prédicat de vérité, = si et seulement si, x, la neige est blanche , « la neige est verte » est vrai, si et seulement si la neige est verte, donc voyez que le prédicat de vérité, la fonction phallique, ça marche même quand l’énoncé est Faux, dire que quelque chose de Faux est Vrai, c’est égal à dire cette chose parce que c’est Faux, …que de le dire !! Donc vous avez là une raison pour laquelle les enfants ne sont pas complètement infondés à dire que leur mère a un phallus, parce qu’est ce qu’ils disent : quand on le voit, il est là le phallus, la fonction de vérité, la fonction identique ça s’appelle, quand il est là, il n’est pas là, et quand il n’est pas là, il est là quand même, V02-52.50 ; quand Hans il dit : ma petite sœur elle a un fait-pipi , il est tout petit, mais quand elle va grandir il va devenir plus grand, les enfants ils font des complications énorme pour arriver avant de découvrir la castration, pour établir que la fonction phallique elle est omniprésente, ... JMV20150602, |
||||||||||||||||||||||||||||||||||||||||||||
| Fonctionnel/Formel | ✔ |
 |
- source w, | |||||||||||||||||||||||||||||||||||||||||||
| Fondement | ✔ |
- crise des fondements, Burali Forti, 1897, c'est la pandémie ... L'argument utilise donc la notion d'ordinal, c’est-à-dire essentiellement celle de bon ordre : il est plus technique que le paradoxe de Russell, bien que son argument ne soit pas si éloigné de ce dernier qui est plus simple à comprendre et à formaliser. Cependant, le paradoxe de Burali-Forti est le premier des paradoxes de la théorie des ensembles à être publié, six ans avant le paradoxe de Russell, et Georg Cantor en fait état dans sa correspondance, ainsi que du paradoxe du plus grand cardinal (dit paradoxe de Cantor), dans les mêmes années. Par ailleurs, le paradoxe de Burali-Forti met directement en jeu la notion d'ordre, et non celle d'appartenance (même si aujourd'hui ces deux notions coïncident pour les ordinaux tels qu'ils sont définis en théorie des ensembles). Ainsi l'incohérence de certaines théories a été établie en dérivant directement le paradoxe de Burali-Forti1. C'est ainsi que John Barkley Rosser a démontré en 1942 l'inconsistance d'une des premières versions des New Foundations2 de Willard Van Orman Quine3 . |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Forcing |
✔ |
- Théorie du forcing, | ||||||||||||||||||||||||||||||||||||||||||||
Forclusion
|
✔ |
- La foclusion, c'est la forclusion de la lisibilité.JMV20150602 - DenreFor, |
||||||||||||||||||||||||||||||||||||||||||||
fort da
|
✔ |
-
Le jeu du fort-da décrit par Freud dans Au-delà du Principe de plaisir (1920) - fort da, |
||||||||||||||||||||||||||||||||||||||||||||
Forme, Formel↑ |
✔ |
- le formel, la forme s'oppose à la matière et présente dans l'histoire de la philosophie une involution qui lui a fait faire un tour complet, depuis l'antiquité jusqu'à l'époque médiévale, d'où la difficulté de lire Spinoza qui y a encore valeur médiévale. Pour Marx, le matérialisme tient à la notion de matière, comme matière d'écriture, comptabilité, système d'écriture. JMV22062010, -la syntaxe, c’est le fait de découper et à partir de là, et là de voir qu’effectivement on peut s’orienter dans un ordre, et la syntaxe, le mot syntaxe, ça veut dire l’ordre, donc la syntaxe, c’est seulement l’aspect syntaxique que vous retrouvez en arithmétique, même en algèbre, même en logique, voyez ça, ( au tableau) ça c’est le fruit de certaines clauses formatives qui sont des clauses formatives dans les systèmes que Smullyan appelle formels, mais que moi j’appelle système d’écriture, parce que je pense que la forme c’est un mot qu’il faudrait bannir, parce que on s’est tellement gargarisé avec formalisation, formel, pourquoi dire qu’on veut formaliser, il y a des gens qui disent que moi, je veux formaliser la psychanalyse, pas du tout, moi, dans la psychanalyse, je pratique une écriture et même mathématique, et il y a une syntaxe, et j’invente même une nouvelle syntaxe pour la logique, pour faire le nœud logique, et que le nœud logique il ne pose pas de grands problèmes de nœuds, il est un plongement de la logique classique dans une logique plus grande, dans une Algèbre de Boole plus grande, JMV23062015, |
||||||||||||||||||||||||||||||||||||||||||||
- SPINOZA, l'Ethique, - Evolution du concept de Forme (Platon, Aristote,(Hylémorphisme, Entéléchie), , Scolastique, Kant,...), W, Cosmovisions, |
||||||||||||||||||||||||||||||||||||||||||||||
Formel (système) ↑ |
✔ |
- systèmes formels, Smullyan.Raymond, (les systèmes formels, le théorème de Gödel et les structures de Tarski, , les îles godéliennes, ...), - Un système formel est une modélisation mathématique d'un langage en général spécialisé. Les éléments linguistiques, mots, phrases, discours, etc., sont représentés par des objets finis (entiers, suites, arbres ou graphes finis…). Le propre d'un système formel est que la correction au sens grammatical de ses éléments est vérifiable algorithmiquement, c'est-à-dire que ceux-ci forment un ensemble récursif. Les systèmes formels s'opposent aux langues naturelles pour lesquels les algorithmes de traitement sont extrêmement complexes et surtout doivent évoluer dans le temps pour s'adapter aux transformations du langage. Les systèmes formels sont apparus en logique mathématique afin de représenter mathématiquement le langage et le raisonnement mathématique, mais peuvent se trouver également dans d'autres contextes : informatique, chimie… - Les systèmes formels ont été conçus par les logiciens afin de poser et étudier mathématiquement certains problèmes liés au langage mathématique. De ce point de vue on peut les considérer comme des métathéories générales, des théories sur les théories (mathématiques). ... Les systèmes logiques visant à modéliser le langage mathématique résolvent trois problèmes :
Les systèmes formels ont permis l'émergence d'une épistémologie des mathématiques appelée point de vue formaliste au terme de laquelle les mathématiques apparaissent comme un jeu de manipulation de symboles suivant des règles rigoureuses mais a priori dépourvues de sens ; le sens des formules est reconstruit a posteriori par les interactions qu'elles entretiennent les unes avec les autres au travers des règles de raisonnement. ... - Une théorie axiomatique est un système logique qui représente une théorie mathématique, c'est-à-dire un ensemble de résultats se rapportant tous à un même type d'objet. Une théorie axiomatique est fondée sur un ensemble d'axiomes qui sont des formules définissant les objets et relations de base de la théorie ; à partir de ces axiomes et en utilisant les règles de raisonnement on dérive les théorèmes de la théorie. Par exemple, la théorie des ensembles est un système formel dont les axiomes définissent la notion d'ensemble. Un axiome est donc une proposition non démontrée qui sert de point de départ à un raisonnement : par exemple « par deux points il passe une et une seule droite » est un axiome de la géométrie euclidienne. La vérité des axiomes ou des formules est définie relativement à un modèle, un univers possible, dans lequel les formules sont interprétées. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
formulaire (langage) ↑ |
✔ |
- Frege (Idéographie, Vrin,) et Frege ci-dessous, - Formule logique, W : En logique on dit d’une suite finie de lettres qu’elle est une formule, ou parfois formule bien formée, d'un langage logique donné lorsqu’elle peut être construite en appliquant une combinaison des règles de la grammaire formelle associée, on parle de la syntaxe du langage. Informellement les formules sont les assemblages de lettres auxquels il est possible de donner une signification en termes de valeur de vérité (Vrai, ou Faux). Les formules logiques sont l'équivalent des phrases du langage naturel. Les formules du langage sont interprétées, suivant la sémantique de la logique considérée, en leur attribuant une valeur de vérité. La syntaxe du calcul des prédicats nécessite d'introduire une autre notion, celle de terme, la syntaxe des termes du langage étant liée à une signature. Les termes sont eux interprétés par des objets (nombres, points, etc.). Il est possible d'assembler les formules pour construire des démonstrations, suivant des règles formelles associées à un système de déduction. L'appellation « formule bien formée » (traduction de (en)well-formed formula) pour formule, est une trace d'un usage ancien où on appelait formules les suites finies de caractères quelconques.
|
||||||||||||||||||||||||||||||||||||||||||||
Formule élémentaire du noeud ↑ |
✔ |
- où P + V = C + 2, Noeud p80 et 137 (Pleins, Vides, Croisements) |
||||||||||||||||||||||||||||||||||||||||||||
Formules de la sexuation ↑
|
✔ |
- Formules de la sexuation, - dans le séminaire Encore et ..., -voir 6 annexes de logique, ici la Table des matières, Lecture des formules kantique de la sexuation 2009 et 2012, JMV, SEPARATION, chapitre III, -Refaire la clinique psychanalytique à partir des formules kantiques de la sexuation , .pdf & enseignement de JMV 2013 - voir Identifications sexuées, |
||||||||||||||||||||||||||||||||||||||||||||
Fou |
✔ |
- le fou c’est celui qui n’a plus la responsabilité de dire oui ou de dire non ! (cas des employés, des militiaires, de certaines conceptions éducatives... de toute subordination autoritariste...impérative) - la folie c’est la méconnaissance, donc vous avez des fous névrosés, des fous pervers, des fous psychotiques, et des fous psychanalystes, les quatre formes du symptôme freudien (névrose, psychose, perversion et psychanalyse) peuvent donner lieu, si les sujets sont fous, il n’y a rien à faire puisque la folie ça ne se guérit pas ! Aujourd’hui on sait rendre les gens fous mais on ne sait pas les arrêter ! Et on ne saura jamais, puisque la folie c’est la méconnaissance, c’est un refus de reconnaître, comment vous pouvez convaincre quelqu’un de reconnaitre, s’il ne reconnait pas ! Pour que ce soit une vraie reconnaissance il faut que ce soit lui qui reconnaisse ! Les fous on ne peut que leurs dire une chose : ou vous vous faites casser la gueule parce qu’on ne vous laissera pas faire, ou bien vous arrêtez d’être fous ! Je dis que c’est la seule façon de parler correctement à un anorexique ou à un addicte, ce sont des héros du désir, ils sont passionnés par la jouissance, mais ils sont fous, mais ils méconnaissent qu’ils sont responsables, JMV20150602, .html, |
||||||||||||||||||||||||||||||||||||||||||||
Frege
Logicisme |
✔ |
-
Frege, il voulait faire une idéographie, Begriffsschrift, ( calcul des propositions et théorie de la quantification), dans la marge pour commenter toutes les démonstrations de l'arithmétique, et il reproche à Boole, d'avoir fait une arithmétique de la logique , parce que du coup il dit qu'il ne peut pas l'utiliser, pour commenter l'arithmétique, parce que du coup il va y avoir deux arithmétiques, donc je vais avoir deux fois le signe plus, deux fois le signe multiplié, deux fois le signe égal, dans la marge et dans le texte et on va confondre JMV09092014, 1.01.40) - Ecrits logiques et philosophiques, G.FREGE, Vrin, 1971, & C.IMBERT, .pdf, |
||||||||||||||||||||||||||||||||||||||||||||
| Freud.Sigmund↑ | ✔ |
- Freud Sigmund, (1856-1939), médecin psychiatre et psychologue humaniste autrichien. Découvre la psychanalyse et l'embaume par le mythe et le sexe, dans une perspective régressive. - La psychnalyse freudienne remplace l'hystérie et est un ancien système de production qui survit dans le nouveau système de production (l'analyse lacanienne). à ce titre le nouage freudien relève de la psychose... - Freud-Lacan, - biblio, - Textes, - Uquac, ebooks Freud, - Valas, - Vocabulaire allemand français , - le rêve chez Freud, - divan, - L'anneau secret !, - Freud invente la cure analytique un procédé pour retourner dans cet autre lieu, qu’il appelle l’Autre scène, l’Inconscient, ce, sans dormir ! Pourquoi il y a de l’inconscient et bien parce que il y a des sujets qui veulent raconter leurs rêves, et ces rêves sont des messages, des textes qui viennent de cette Autre scène, qui est structurée par une autre logique, par une autre syntaxe, donc il faut étudier pour chacun la pratique, c’est pas un savoir, moi je ne fais pas des analogies avec ça, je prétends pas du tout, et je dis que dans l’écriture, ça ( en désignant les diagrammes de 3 ronds au tableau) , étudier la Logique modifiée à côté de la Logique classique c’est formateur, ça me permet à moi, d’être épaté par le fait que ça s’efface, ...JMV20150602; |
||||||||||||||||||||||||||||||||||||||||||||
| G | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
| GALOIS.Evariste, | ✔ | Évariste Galois est un mathématicien français, né le 25 octobre 1811 à Bourg-Égalité (aujourd’hui Bourg-la-Reine) et mort le 31 mai 1832 à Paris. Son nom a été donné à une branche des mathématiques dont il a posé les prémices, la théorie de Galois. Il est un précurseur dans la mise en évidence de la notion de groupe et un des premiers à expliciter la correspondance entre symétries et invariants. Sa « théorie de l'ambiguïté » est toujours féconde au XXIe siècle. Mort à la suite d'un duel, apparemment galant, à l'âge de vingt ans, il laisse un manuscrit élaboré trois ans plus tôt, dans lequel il établit qu'une équation algébrique est résoluble par radicaux si et seulement si le groupe de permutations de ses racines a une certaine structure, qu'on appellera plus tard résolublea. Ce Mémoire sur les conditions de résolubilité des équations par radicaux, publié par Joseph Liouville quatorze ans après sa mort, ainsi qu'un article Sur la théorie des nombres paru alors qu'il avait dix-neuf ans, ont été considérés par ses successeurs, en particulier Sophus Lie, comme le déclencheur du point de vue structural et méthodologique des mathématiques modernes. |
- GALOIS.Evariste, W, | |||||||||||||||||||||||||||||||||||||||||||
Galois (Corps de ) |
✔ |
- Mais ici nous allons nous apercevoir que nous allons utiliser les termes de module pour les groupes, algèbre pour les anneaux, et espace vectoriels pour les corps, et que ça permet de distinguer ce que nous allons faire, et ce qu’a fait Guitart, qui lui est parti de ce corps là, et voilà ce qu’il a fait, il a construit : l’algèbre de Boole, c’est ce que je suis en train d’essayer de construire, 1.22.34, et puis il a construit aussi les espaces vectoriels, qui s’appellent les corps de Galois, et qui ne sont pas très compliqués à construire puisqu’ils sont, ont les écrit comme ça, GF(2n) ; ça veut dire pour un anglais Galois Fields 2n, et ce qu’il a montré c’est qu’il y avait une corrélation entre les deux, ce qui fait que c’est la première fois à ma connaissance, mais à la connaissance des mathématiciens, qu’on établit une relation entre Galois et Boole, JMV27012015, -le nœud logique il ne pose pas de grands problèmes de nœuds, il est un plongement de la logique classique dans une logique plus grande, dans une Algèbre de Boole plus grande, au lieu d’être uniquement dans Z2, comme ça, Z2 c’est 0,1, avec l’addition et la multiplication, +, x, c’est un anneau de Boole, et celui là c’est le plus petit, c’est un corps de Boole, et si on plonge cette logique classique, tout ce qu’on fait avec ce 0 et ce 1 ; dans Z2 puissance n, Z2n, donc vous avez 0, 1, à la puissance n, et vous avez + et x, là c’est plus un corps ce sont des anneaux de Boole, mais Guitart a montré qu’à partir de là, on pouvait aussi faire des extensions de corps, donc à partir de Z2, le plus petit, et qu’on obtenait des corps de Galois, ça s’appelle GaloisField en anglais, 59.37, 2 puissance n, 2n, de caractéristique 2, vous voyez que le 2 joue un rôle, mais ne confondez pas ce 2 qui ici, est un élément qui est dit caractéristique, la caractéristique c’est le nombre qui multiplie n’importe quel élément pour donner zéro, donc l’algèbre de Boole, que ce soit la plus petite qui est un corps, ou les anneaux de Boole et les Algèbres de Boole la structure linéaire, ça c’est de caractéristique 2, et les corps de Galois de caractéristique 2 correspondent à des Algèbres de Boole, ça on peut appeler ça Algèbre de Boole, AB (2n), des algèbres de Boole de plus grand cardinal que simplement 2, ici, vous avez une toute petite algèbre avec 0,1, (nœud logique), seulement, 1.00.29, je vous ai écrit au tableau les deux formules du plus et du multiplier, le plus c’est o, 1 qui va nous donner 0, 1 et ici du 0, je répète que je vous ai donné un moyen de rendre ça plausible, pour votre pratique, pour que vous ayez les coudées franches pour pourvoir apprendre à compter, à faire de l’algèbre de Boole sans être un ordinateur, sans être obligé de vous transformer en automate,... JMV23062015, L475 |
G, Apport de GALOIS aux mathématiques, W, |
|||||||||||||||||||||||||||||||||||||||||||
✔ |
- généralisation en mathématique et logique (selon wiki). Il arrive souvent dans l'histoire des mathématiques qu'une notion apparaisse d'abord dans un domaine précis, puis se voit transposée à d'autres domaines, et enfin généralisée à un domaine plus large, dont le domaine primitif ne soit qu'un cas particulier. - Mais Lacan semble invalider cette approche, dans La science et la Vérité, E869 : théorie généralisée ne saurait nullement être pris pour vouloir dire : passage au général, et dans L'Etourdit AE481 : un champ ne procède pas de la généralisation, mais de remaniement topologiques, d'une rétroaction sur le commencement telle qu'elle en efface l'histoire. Cité par JMV dans "ça claque". - Bog, pour Borromeen généralisé, (abréviation sur ce site), suite des définitions |
|||||||||||||||||||||||||||||||||||||||||||||
Génératrice, chaine |
✔ |
Chaine borroméenne ET de Whitehead, B + W, (pas de noeud), qui vont permettre de produire tous les noeuds (JMV10062014-12'.30").
|
||||||||||||||||||||||||||||||||||||||||||||
| Géométrie euclidienne | ✔ |
La géométrie euclidienne commence avec les Éléments d'Euclide, qui est à la fois une somme des connaissances géométriques de l'époque et une tentative de formalisation mathématique de ces connaissances. Les notions de droite, de plan, de longueur, d'aire y sont exposées et forment le support des cours de géométrie élémentaire. La conception de la géométrie est intimement liée à la vision de l'espace physique ambiant au sens classique du terme. Les conceptions géométriques connaissent, depuis les travaux d'Euclide, des évolutions suivant trois axes principaux :
Plus de 2 000 ans après sa naissance, l'espace géométrique euclidien est un outil toujours efficace aux vastes domaines d'applications. À l’exception des échelles cosmiques et microscopiques, l'espace des physiciens reste encore principalement du domaine de la géométrie euclidienne. Son aspect mathématique est traité de manière didactique dans l'article produit scalaire. L'article se fonde sur la formalisation d'un vecteur à l'aide d'un bipoint, développé dans vecteur. Une approche plus poussée, fondée sur la formalisation axiomatique de l'espace vectoriel est développée dans espace euclidien. |
||||||||||||||||||||||||||||||||||||||||||||
| des géométries, sa fonction, W, | ||||||||||||||||||||||||||||||||||||||||||||||
| Géométrie algèbrique, | ✔ |
La géométrie algébrique est un domaine des mathématiques qui, historiquement, s'est d'abord intéressé à des objets géométriques (courbes, surfaces…) composés des points dont les coordonnées vérifiaient des équations ne faisant intervenir que des sommes et des produits (par exemple le cercle unité dans le plan rapporté à un repère orthonormé admet pour équation x2 + y2 = 1 ). La simplicité de cette définition fait qu'elle embrasse un grand nombre d'objets et qu'elle permet de développer une théorie riche. Les besoins théoriques ont contraint les mathématiciens à introduire des objets plus généraux dont l'étude a eu des applications bien au-delà de la simple géométrie algébrique ; en théorie des nombres par exemple, cela a conduit à une preuve du grand théorème de Fermat. Cette branche des mathématiques n'a désormais plus grand-chose à voir avec la géométrie analytique dont elle est en partie issue.
Les mille paysages de la géométrie algèbrique, CNRS, P.DANCHIN, C.FERMANIAN KAMMERER |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Géométrie analytique, | ✔ | La géométrie analytique est une approche de la géométrie dans laquelle les objets sont décrits par des équations ou des inéquations à l'aide d'un système de coordonnées. Elle est fondamentale pour la physique et l'infographie. En géométrie analytique, le choix d'un repère est indispensable. Tous les objets seront décrits relativement à ce repère. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Géométrie descriptive, | ✔ |
- Géométrie descriptive et anamorphoses, Chantal GABRIEL-RANDOUR, & J.DABRE, - Origine de la géométrie projective, en espagnol |
- |
|||||||||||||||||||||||||||||||||||||||||||
Géométries |
✔ |
- Fonction de la géométrie, R.Thom - Qu'est-ce qu'une géométrie ? - Joyce et la géométrie - Langage , mathématique et topologie, - La topologie selon Listing, - Topologie et dimensions et mouvements, - La topologie, - histoire de la topologie, - Origine de la géométrie projective, en espagnol - Le DI, la droite infinie, 2006, J-M.V - géométrie des Grecs ....aux dimensions supérieures, - Symétries et groupes, - Afin de préciser le narcissisme, JMV, 2007, Intrinsèque extrinsèque, la géométrie, la symétrie, la symétrie miroir, L'envers du narcissisme, - Lire "L'origine de la géométrie" (.pdf) de Husserl, et critique de JMV |
||||||||||||||||||||||||||||||||||||||||||||
Géométries |
✔ |
- La géométrie est nettement distincte de de la topologie, mais avec des points de contact et des appréciations mutuelles ( Essaim voir p 143) . Géométrie classique : Inaugurée par les Grecs, cette étude est fondée sur la logique et considère les objets de l'espace, et vise à donner un exposé axiomatique et déductif. Voir les "Eléments d'Euclide" Essaim p23 Géométrie analytique : Existe au début du second tour de la métaphysique occidentale, une renaissance de la tradition ecuclidienne avec Galilée. Mais la géométrie analytique est attachée au témoignage de Descartes, qui initie le mouvement scientifique qui s'achève sous nos yeux. La géométrie analytique est en défaut sur un point : non qu'elle s'attache à l'algèbre au détriment du dessin, mais elle s'attache trop servilement à une algèbre spécifique et réduite (algèbre classique, harmonique) au détriment de la structure. Défaut encore actuel dans l'enseignement. Essaim p 24 - la géométrie du Moi, se définit par la géométrie classique (euclidienne et cartésienne). La topologie du sujet n'exclut pas que l'on sache ce qu'est une géométrie depuis 1872, moment de son achèvement. Essaim p 12. - Lacan et les Mathématiques, & Langage, |
||||||||||||||||||||||||||||||||||||||||||||
Géométrie des non-nœuds |
✔ |
- Géométrie au sens de Félix Klein, catégorie dit-on aujourd'hui. Définie par Une multiplicité d'objets, les Transformations permises, (B1, M2, T3, et le mouvement nœud N3). Voir cas d'identité entre une chaine et l'enlacement simple dont elle possède le même invariant Noeuds p8 Et l'invariance de la répartition du nombre d'enlacement. Les invariants sont : Conséquences : |
Quatre mouvements dans le noeud, Reidmaster, |
|||||||||||||||||||||||||||||||||||||||||||
| GIRARD.J-Y | ✔ |
Logicien, voir GIRARD, | ||||||||||||||||||||||||||||||||||||||||||||
| Gödel, | ✔ |
avec le paradoxe de Gödel :
|
||||||||||||||||||||||||||||||||||||||||||||
Grammaire |
✔ |
- la logique au niveau de la coordination, c’est de la grammaire, mais les grammairiens abandonnent ça aux logiciens parce que, il y a une histoire de vérité qui va apparaître, un calcul sur le Vrai et le Faux, |
||||||||||||||||||||||||||||||||||||||||||||
Gramme ↑ |
✔ |
- voir graphe - gramme de Lacan ( graphe du désir, p817, Subversion du sujet..., E793, Lacan); - graphe du désir augmenté , |
||||||||||||||||||||||||||||||||||||||||||||
Graphe↑ |
✔ |
- le graphe du désir, sur la sphère, puis sur le tore |
||||||||||||||||||||||||||||||||||||||||||||
Graphe de Terrasson |
✔ |
- Noeud, p 41,76,339 - le graphe de Terrasson, dans le noeud, repésente un axe de symétrie entre la partie noeud et la partie non-noeud du noeud ! Il peut être présenté sous forme de Droite infinie, DI, (voir JMV23092014, 31.00) |
||||||||||||||||||||||||||||||||||||||||||||
Groupe fondamental du noeud |
✔ |
- G, pour Groupe fondamental, Noeud p13, Essaim p167 - le groupe fondamental d'un espace donné est un invariant au travers des transformations continues relevant de ce type d'études ou d'explorations qui cherchent à associer des structures de l'algèbre à des objets de la topologie." ça claque ", p52, JMV, 1998, sur Cairn info - objet du livre Essaim , - voir |
||||||||||||||||||||||||||||||||||||||||||||
| Groupe, | ✔ |
- Groupe mathématiques, W, - Axiomatiquement un groupe est un ensemble muni d'une loi de composition interne (x,y) -->x*y associative, telle qu'il existe un élément privilégié e, appelé élément neutre, tel que x*e = e*x = x et tel que tous les éléments aient un inverse (c-à-d que pour tout x il existe un élément y tel que x*y = y*x = e). Un tel groupe est dit abélien ou commutatif, si x*y = y*x . (Dictionnaire des mathématiques, T1, p14, EU, Albin MICHEL), - Ensemble d'éléments (au moins deux !) muni d'un loi interne. et on les connait bien ceux là, les espaces vectoriels, parce que ça sert en géométrie, avec les vecteurs, c’est pour ça que ça s’appelle espace vectoriel, on a appris ça en mécanique, celle de Newton, la mécanique se fait dans un espace vectoriel, JMV27012015, - Groupe géométrique, W, -Groupe de rotation, de permutation - Introduction à la topologie, Etude préliminaire à la topologie, Johann Benedict LISTING, |
||||||||||||||||||||||||||||||||||||||||||||
Groupe fondamental d'une surface ↑ |
✔ |
- est le groupe qui forme les classes de lacets (coupures) homotopes dans la surface prise comme espace (lacets orientés et pointés, ont tous même origine). | ||||||||||||||||||||||||||||||||||||||||||||
Groupe eulérien ↑
|
✔ |
- Esssaim p 29 | ||||||||||||||||||||||||||||||||||||||||||||
Groupe de Klein ↑
|
✔ |
- Essaim p 30 - voir Klein , - voir Fantasme |
||||||||||||||||||||||||||||||||||||||||||||
| Groupe de Li, | ✔ | - Groupe de Li, - Groupe de Li et R.THOM, - Un groupe de Lie est un groupe — au sens mathématique — continu (c'est-à-dire dont chaque élément est infinitésimalement proche d'au moins un autre élément). sur Techo-Science, |
||||||||||||||||||||||||||||||||||||||||||||
✔ |
- Guitart René, -la découverte de René Guitar en matière d’Algèbre et de Logique ! Ce que je vise c’est que Guitar va me permettre de comprendre ce que je ne comprenais pas quand on commence à compliquer un peu la logique modifiée, |
|||||||||||||||||||||||||||||||||||||||||||||
| H | ||||||||||||||||||||||||||||||||||||||||||||||
| Harmonie | ✔ |
- Il n'y a ni harmonie sexuelle, ni harmonie dans les sciences, ni harmonie en général, sauf à maquiller les résultats à l'aide d'une mise en scène ! L'harmonie est une illusion qui relève de la prestidigitation, de la suggestion et d'un tempon idéologique. Idéologie grecque, où d'admirables perspectives se referment dans votre dos sans prévention ! Masque de l'Inconscient ! | ||||||||||||||||||||||||||||||||||||||||||||
| Hauptsatz | ✔ |
- Hauptsatz ≡ Théorème de Herbrand, (≡ pour équivaut) Théorème de Herbrand : En logique, le théorème de Herbrand, publié en 1930 par Jacques Herbrand, établit un lien entre la logique du premier ordre et la logique propositionnelle (qui peut-être vu comme la logique d'ordre zéro). La validité (ou prouvabilité) d’une formule du premier ordre se ramène à la validité (ou prouvabilité) d'un ensemble fini de formules propositionnelles. |
||||||||||||||||||||||||||||||||||||||||||||
| Hénologie | ✔ |
- Science de l'Un, - Hénologie, - voir, Vide, Non-être, Incorporels, |
||||||||||||||||||||||||||||||||||||||||||||
| HERBRAND | ✔ |
Jacques Herbrand, né à Paris le 12 février 1908 et mort dans un accident de montagne à La Bérarde en Oisans (Isère), le 27 juillet 1931, est un mathématicien et logicien français. Reçu deuxième au concours de l'École normale supérieure en 1925, il est premier à l'agrégation de mathématiques en 1928. Il rejoint l’armée en octobre 1929 pour faire son service militaire, puis soutient sa thèse à la Sorbonne en 1930, devant un jury présidé par Ernest Vessiot. En 1930-1931, une bourse de la Fondation Rockefeller lui permet de se rendre en Allemagne pour étudier d’abord à Berlin avec John von Neumann, puis à Hambourg avec Emil Artin, et enfin à Göttingen avec Emmy Noether. Signalons aussi qu'il n'a pu relire son manuscrit Le développement moderne de la théorie des corps algébriques : corps de classes et lois de réciprocité (Mémorial des sciences mathématiques, fasc. LXXV, 72 pages, Gauthier-Villars, 1936), qui a été relu par Claude Chevalley pour sa publication posthume et discuté en cette occasion avec Jean Cavaillès. Ces aspects de la théorie du corps de classes seraient à préciser, notamment en ce qui concerne un autre « théorème de Herbrand » de nature cohomologique sur les unités des corps de nombres, de grande importance et très souvent utilisé et généralisé, le fameux quotient de Herbrand (en). Il n'en laisse pas moins son nom à deux autres théorèmes, le théorème de Herbrand-Ribet, en théorie des nombres, et le théorème de Herbrand, en logique. Il est à l'origine du « modèle de Herbrand-Gödel » des fonctions récursives. Selon le mathématicien Claude Chevalley, « Jacques Herbrand aurait détesté Bourbaki3 ». Une exposition4 lui a été consacrée à l'École normale supérieure, à l'occasion du centenaire de sa naissance. |
||||||||||||||||||||||||||||||||||||||||||||
| Herbrand, Théorème de, | ✔ |
En logique, le théorème de Herbrand, publié en 1930 par Jacques Herbrand, établit un lien entre la logique du premier ordre et la logique propositionnelle (qui peut-être vu comme la logique d'ordre zéro). La validité (ou prouvabilité) d’une formule du premier ordre se ramène à la validité (ou prouvabilité) d'un ensemble fini de formules propositionnelles. Alors qu'il est possible de déterminer algorithmiquement si une formule propositionnelle est démontrable ou pas, on sait — depuis les travaux de Gödel, Tarski, Church, Turing et autres — que la même question pour les formules du premier ordre est indécidable. Le théorème de Herbrand montre qu’elle est cependant semi-décidable : bien qu’il n’existe pas d’algorithme qui détermine si une formule donnée est prouvable ou pas, il existe une procédure qui résout partiellement la question en répondant « oui » si et seulement si la formule donnée est prouvable (pour certaines formules non prouvables, le calcul ne s'arrête pas). W, |
||||||||||||||||||||||||||||||||||||||||||||
Hexagramme |
✔ |
- Hexagramme ou Chaine dite de "David", voir Chaine de David, ( voir Pentagramme) (usages), ou Etoile de David ou Bouclier de David, composée de deux triangles équilatéraux superposés, l'un la pointe vers le haut, l'autre vers le bas,. Ou Sceau de Salomon, Etoile de Sion, Triangle de Salomon. | ||||||||||||||||||||||||||||||||||||||||||||
Histoire |
✔ |
- l'Histoire c'est la science de l'embarras ! (faire parler les morts !) - Histoire des mathématiques, de la Logique, JMV23062015 |
||||||||||||||||||||||||||||||||||||||||||||
| Homéomorphie↑ | - Equivalence topologique entre deux courbes, peut s'étendre à leur voisinage dans l'espace p 19 | |||||||||||||||||||||||||||||||||||||||||||||
Homologie↑ |
✔ | - Relation d'équivalence définie entre des objets qui peuvent présenter un nombre de ronds différents Noeud p318 - Les noeuds propres sont à coupure constante, du fait d'être constitué d'un seul élément de corde. |
||||||||||||||||||||||||||||||||||||||||||||
| Une première approche, qui reste proche de l’intuition géométrique décrite ci-dessus, consiste à suivre l’idée du bordisme. Cette approche fonctionne très bien en dimension 1 et peut servir d’introduction à l’homologie. Elle n’est toutefois pas complètement fidèle à l’esprit de Poincaré, et possède surtout un défaut majeur : en dimension plus grande, elle diffère de l’homologie. Cependant, le début de la théorie du bordisme fait une bonne introduction à l’homologie. suite sur .... in Analysis Situs, HPdSG, in Topologie algébrique des variétés, |
||||||||||||||||||||||||||||||||||||||||||||||
Homotope↑ |
✔ | Lacet, équivalent par déformation continue, cela ne s'opposant pas à ce qu'il se recoupe en eux même, Etoffe p117 | ||||||||||||||||||||||||||||||||||||||||||||
Homotopie↑
|
✔ |
- L'homotopie est une transformation d'immersion qui autorise l'inversion d'un croisement à condition qu'il soit un croisement propre, soit d'un même composant de ficelle. " ça claque " p50, JMV revue Essaim. - Mouvement d'inversion d'un dessus dessous entre deux brins d'un noeud propre. - voir mouvements noeud - l’homotopie c’est quand on passe en dimension quatre, l’homotopie en dimension trois, c’est un modèle de ce qu’il se passe en dimension quatre, JMV23092014,.html, (2), 2.10.00 |
||||||||||||||||||||||||||||||||||||||||||||
| Hybride (mouvement noeud) ↑ |
✔ |
- mouvement noeud hybride, noté Nh, ou mouvement de Whitehead, ou quart de tour. (en lien à Kant avec Sade) - introduit un couple de ronds noués dans le borroméen, ou crée entre deux ronds un lien-couple que l'on associe à la structure du fantasme, pour décrire la réversibilité des ronds, des points de vue ! |
||||||||||||||||||||||||||||||||||||||||||||
| Hystoricité | ✔ |
- voir Tore - Joyce Hystorique - L'Histoire c'est la science de l'ambarras ....! Faire parler les morts ....! |
||||||||||||||||||||||||||||||||||||||||||||
| I | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
| Imaginaire | ✔ |
- L'imaginaire, son espace de constructions optiques géométrique, de leurre, s'origine dans la symétrie plane du miroir, et relève tant de la dimension deux (des surfaces) que de la présence de l'autre, "d'eux" ! Lieu sans temporalité, ni topos, ni précison. Cet espace est structuré par l'apparition et le disparition de traits. Entre corps et image, le pénis médium présent ou absent, ainsi que l'autre imginaire, rival ou idéal, non sans tensions subjectives habitées par l'angoisse. C'est le lieu fondateur de la connaissance paranoïaque du sujet dont les modes imaginaires donnent sa consistance à la connaissance spéculaire (l'image spéculaire c'est i(a), l'autre du miroir, mon porchain ou moi même, et enveloppe l'objet a).. Cet espace est distinct du repérage du fantasme. L'imaginaire est à situer dans la topologie du sujet. Le schéma de Freud dans la lettre 52, devient le graphe de ligne (temporel) de l'appareil psychique qui sera articulié par Lacan dans le schéma R puis F et L avec sa fermeture proposée par J-M.Vappereau. d'après Etoffe p 16 à ... 49 ! - L'imaginaire c'est le corps ! - dans le schéma L, Lacan situe la relation imaginaire entre a et a'. Le gril imaginaire c'est aa'. Ep55. - L'imaginaire est du type de la fonction des nombres complexes dans la résolution des équations algébriques. Etoffe p21 - Les effets par quoi l'organisme subsiste, c'est ce par quoi nous sommes forcés de concevoir l'imaginaire ; quelque chose lui indique que tel élément de l'extérieur, du milieu, de l'Umwelt comme on dit est absorbable ou plus généralement propice à sa conservation. Cela veut dire que l'Umwelt est une sorte de halo, de double de l'organisme, et puis c'est tout. C'est ça qu'on appelle l'imaginaire.(p514) (Lacan Aa 07051969) |
||||||||||||||||||||||||||||||||||||||||||||
| Immersion | ✔ |
- plongement c’est-à-dire qu’on met un objet dans un espace plus grand, et plongement ça veut dire que la transformation de l’objet initiale, le rond ou les ronds, on plonge dans l’espace la fonction mathématique qu’on emploie si elle est injective, si elle n’est pas injective, ça s’appelle pas un plongement, ça s’appelle une immersion. - Une application f : X → Y entre deux espaces topologiques est un plongement de X dans Y si elle induit (par corestriction) un homéomorphisme de X dans f(X) (muni de la topologie induite).
- Voir SMALE.S, ci-contre
|
- W, plongement - W, Immersion, - SMALE.S, Cronomaths, |
|||||||||||||||||||||||||||||||||||||||||||
Impropre (noeud) ↑ |
✔ |
- Les nœuds propres et impropres se répartissent en deux familles dites Trèfles et Listing Np81 - Classification Noeuds et Chaines alternables, gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
Implication↑
|
✔ |
-
Relation logique entre deux phénomènes telle que la vérité ou la réalité de l'un fait connaître avec certitude la vérité ou la réalité de l'autre. Implication réciproque, simple, stricte. Tout ce que la vie contenait d'abord à l'état d'implication réciproque ( Bergson , Évol. créatr., 1907 , p. 118) CNLRT, -linguistique : Implication entre deux propositions. Relation telle que, la première étant vraie, la seconde est nécessairement vraie. CNLRT - ⇒, ⇔, - Clef pour la passe, 1ere partie, argument 3, dans L'amour du tout, JMV, de l'implication des logiciens ... |
||||||||||||||||||||||||||||||||||||||||||||
| Implication girardienne | ||||||||||||||||||||||||||||||||||||||||||||||
| Inconscient | ✔ | - L'inconscient est cette partie du discours concret en tant que transindividuel, qui fait défaut à la disposition du sujet pour rétablir la continuité de son discours conscient. p 258, Ecrits, Fonction et Champ de la Parole et du Langage, LACAN, 1953, Seuil, - L'insconscient est ce chapitre de mon histoire qui est marqué par un blanc occupé par un mensonge : c'est le chapitre censuré. Mais la vérité peut être retrouvée; le plus souvent déjà elle est écrite ailleurs. A savoir : * Dans les monuments : et ceci est mon corps, c'est-à-dire le noyau hystérique de la névrose où le symptôme hystérique montre la structure du langage et se déchiffre comme un inscription qui, une fois recueillie, peut sans perte grave être détruite. * Dans les documents d'archives aussi, et ce sont les souvenirs de mon enfance, inpénétrables aussi bien qu'eux, quand je n'en connais pas la provenance. *Dans l'évolution sémantique; et ceci répond au stock et aux acceptions du vocabulaire qui m'est particulier, comme au style de ma vie et mon caractère; * Dans les traditions aussi, voire dans les légendes qui sous une forme héroïsée véhiculent mon histoire; * Dans les traces, enfin, qu'en conservent inévitablement les distorsions, nécessitées par le raccord du chapitre adultéré dans les chapitres qui l'encadrent, et dont mon exégèse rétablira le sens. p 259, Ecrits, Fonction et Champ de la Parole et du Langage, LACAN, 1953, Seuil, |
||||||||||||||||||||||||||||||||||||||||||||
| - Inconscient sur Lutécium, J.SIBONI, | ||||||||||||||||||||||||||||||||||||||||||||||
| - Le langage est la condition de l'inconscient, et l'inconscient est la condition de la linguistique, s'il n'y a pas de lecture de l'inconscient , il n'y a pas de linguistique. JMV23062015 - = "il est faux Cs. et il est faux non-Cs". - l'Inconscient n'est pas le non-conscient -Freud - lire Position de l'inconscient lacan Ecrits p829 ou 193 - l'Inconscient mutera en Ça dans la deuxième topique de Freud , Topiques, sur gaogoa, Lettre 52, 1ere topique, 2d topique, - effet de langage - remplacer l'Inconscient (Ics) par le parlêtre - c'est de ça que je supporte l'Inconscient, de la copulation du langage avec notre propre corps p3 le Sinthome 16031976, Lacan, - L'amour du tout, partie 3, JMV 1992 - L'inconscient freudien en équation, in Eros et psyché, 1ere partie, JMV, 2012, - Ouverture et fermeture de l'inconscient JMV20-01-2015 (MP3), (La fermeture , c'est l'évènement psychique de Freud, ou l'acte de Lacan, l'inconscient devient circuit fermé, si ça s'ouvre ça provoque une destitution subjective, un ruissellement, une maladie dans le corps, un délire, ...) |
||||||||||||||||||||||||||||||||||||||||||||||
| - Eros et Psyché, JMV (II-Argument IV), ( le mode mineur de l'écriture de la vérité) + 3casplus !? L'écriture de l'Ics.freudien en logique. De la loi de vérité intrinsèque au calcul ( Tarsky, Hans, et Wundt ) à l'écriture de l'Ics. de Freud : sa contruction littérale dans la logique modifiée en topologie du sujet. Ou comment contredire Wundt (Locke) en raison. - je peux construire l’inconscient freudien, je peux dire que la conscience, niée par cette négation, c’est équivalent comme le dit Freud, et il a beaucoup de mal avec ça, c’est équivalent à la non conscience, et à la non non conscience.  Ce qui fait dire à Freud que l’Inconscient, ça c’est l’inconscient, n’est pas le non conscient, c’est le non (¬) conscient et quelque chose dont il est faux de dire (¬ ) qu’il est non (~) conscient, donc je le lis comme ça : Il est faux de dire que c’est conscient, et il est faux de dire que c’est non conscient. L’inconscient c’est un truc intermédiaire qui va se trivialiser très rapidement, à cause de cet axiome de van Belinghen, vous pouvez à partir de cet axiome, démontrer l’énoncé suivant que - l’objection que fait Wundt à Freud, il lui dit on ne peut pas parler d’Inconscient parce que si l’inconscient c’est équivalent au non conscient, alors c’est du non psychisme, le psychisme inconscient équivalent à du non psychisme, le psychisme inconscient équivalent à du non conscient ça équivaut à du non psychisme, ce qui ne voit pas Wundt c’est qu’on peut ici changer les négations modifiées, les prendre dans un autre nœud, qui n’est pas le même nœud que celui dans lequel on est en train d’écrire toute la phrase, ce qui se fait en logique en général, Wundt il ne pouvait pas imaginer des choses comme ça, ça confirme que Freud a raison de maintenir que si on en a pas la pratique, qui est pour Freud une pratique de langue parlée, il analyse les rêves dans la langue parlée, - pour WUNDT lire Wundt gaogoa, in Logique, & Wundt gaogoa, in Langage, |
||||||||||||||||||||||||||||||||||||||||||||||
Incorporation↑
|
✔ |
- L'évènement premier de l'incorporation a pour effet insurmontable le refoulement originaire. - L'incorporation répond à la prématuration du mammifère humain qui constitue la composante réelle de ce qui le caractérise. Cette déficience organique fait du mammifère humain un être foncièrement arriéré ! C'est par le recours au signifiant, à la structure du langage qu'il tente de surmonter cette insuffisance ! Etoffe p28 - Corps, incorporation et incorporelles, JMV, 2010 - dans la réponse à la Question II il va introduire la version dogmatique, puisque c’est écrit, mais définitive de la doctrine de l’incorporation, c’est là qu’il parle des incorporels, c’est là qu’il parle de la barre, il n’en a jamais parlé comme ça, il dit que les incorporels qu’ont découvert les stoïciens, c’est ce qui fait tenir le langage au corps, JMV16062015, |
||||||||||||||||||||||||||||||||||||||||||||
✔ |
- L'incorporation c'est un corps symbolique qui rentre dans le corps au sens naïf, c'est ce qu'il faut reconnaitre avec Lacan dans Radiophonie, comme la behajung, le jugement d'attribution (L62p1, JMV18022014) -L’incorporation il en parle dans Radiophonie, question II, il en parle 3 fois dans le séminaire, Relation d’objet, l’Ethique, et Problème Cruciaux, , il emploie le mot, 2 ou 3 fois dans les Ecrits, il va partir de l’incorporation orale phallique, dans la Relation d’objet, ce qui va le conduire ensuite à poser la question : qu’est ce que c’est que ça ?, sans le dire comme ça, il va dire dans l’Ethique, mais qu’est ce qu’on mange ?, l’incorporation orale, mais qu’est ce qu’on mange ?, là il va introduire la notion du Livre, de manger le Livre, manger du signifiant, manger la phallus comme signifiant, 27.36, et puis dans Problèmes cruciaux, il va conclure de cette manière là, il s’agit bien de manger la lettre du signifiant, c’est-à-dire le phonème, et il va écrire le texte princeps sur l’incorporation dans Question II de Radiophonie, si vous voulez avoir une vue assez serrée de ce dont parle Lacan, juste avant il dit des choses sur la réalité, la réalité de la présence de la lettre dans le monde, je ne vais pas m’étendre là-dessus, des formules mathématiques qui habitent le monde, c’est déjà assez intéressant, ça modifie tout à fait ce qu’on peut faire et ce qu’on va découvrir avec les nœuds, JMV20150602, |
|||||||||||||||||||||||||||||||||||||||||||||
Incorporel
Incorporelle ↑ |
✔ |
- les incorporels, c'est ce qui rend lisible le signifié, Radiophonie, 1970, -dans la réponse à la Question II Lacan va introduire la version dogmatique, puisque c’est écrit, mais définitive de la doctrine de l’incorporation, c’est là qu’il parle des incorporels, c’est là qu’il parle de la barre, il n’en a jamais parlé comme ça, il dit que les incorporels qu’ont découvert les stoïciens, c’est ce qui fait tenir le langage au corps, - Incorporels et incoporelles, - les incorporels .... - Etoffe p28 - Corps, incorporation et incorporel, J-M.Vappereau, - Pascal a fait un relevé des tous les éléments incorporels dans Bréhier, qui sont beaucoup plus vaste ( Style, manière d'être, harmonie..) que ce qu’on dit en général du vide, du temps, et du lekton ; Bréhier le lekton, il l’appelle l’exprimable, Lacan reprend le terme grec en l’écrivant en latin, mais de quoi s’agit-il, Lacan va ajouter 3 incorporel(le)s, mais qui sont au féminin, il introduit : la fonction pour les mathématiques, l’application pour la topologie, alors c’est typiquement du Lacan il fait une confusion entre théorie des ensembles et la topologie, à cause de la topologie générale, il dit pour la topologie, mais les applications c’est la théorie des ensembles, et le troisième c’est quoi, pour la logique, Jacques : l’analyse, JMV : oui, l’analyse pour la logique, donc il donne trois incorporel(le)s qui sont au féminin, ça élargit un peu les choses, c’est pas spécialement au masculin, Alors ces incorporels, qu’elle est la meilleur définition pour apprécier ce que sont les incorporels, et pour voir les difficultés du paranoïaque avec ça, vous pouvez lire ça dans des cours de philo !, il y a des textes qui définissent les incorporels comme ce que l’étranger ne peut pas comprendre, JMV16062015, - et langage, et narcissisme, JMV20150602 p17, |
||||||||||||||||||||||||||||||||||||||||||||
| Inférence | Mouvement de pensée allant des principes à la conclusion. | |||||||||||||||||||||||||||||||||||||||||||||
| Infini | ✔ |
- Ce qui est non terminé, |
||||||||||||||||||||||||||||||||||||||||||||
| - L'infini, c'est la DI, la droite infinie, celle de l'axe orthonormé de la géométrie euclidienne, .. il y a toujours de l'espoir..., Voir vocabulaire de topologie Nodologie... L'axe de toute les religions, de toutes les politiques, demain ...demain, tous les espoirs sont permis.... la Dei !! Le Dieu de la procrastination... - Comment se ferme le noeud .... dans l'Inconscient ....? La question du nouage (RSI, au mieux borroméen) est donc une inconnue qui telle une planète invisible mais influente oriente l'axe du destin personnel. L'objet (ou son absence) focal de ce nouage, est idéalement un signifiant, qui ruissellera, ou surgira dans le discours du sujet sous forme de signifié ... mais cela peut être un tout autre objet du désir ...., alors le noeud disparait, de n'être plus noué ...pour se reformer autour, dans un autre signifiant .... - Psychanalyse et mathématique, Freud contemporain de Cantor, JMV, 2007 |
voir D.I, JMV |
|||||||||||||||||||||||||||||||||||||||||||||
| - L'infini et l'Univers, W, | ||||||||||||||||||||||||||||||||||||||||||||||
| Informatique & mathématiques, | - - fourier-Parisse, - GIRARD.J-Y, |
|||||||||||||||||||||||||||||||||||||||||||||
| - Binaire, gaogoa, | ||||||||||||||||||||||||||||||||||||||||||||||
| Informatique théorique | ✔ | L'informatique théorique est l'étude des fondements logiques et mathématiques de l'informatique. C'est une branche de la science informatique. Plus généralement, le terme est utilisé pour désigner des domaines ou sous-domaines de recherche centrés sur des vérités universelles (axiomes) en rapport avec l'informatique. L'informatique théorique se caractérise par une approche par nature plus mathématique et moins empirique de l'informatique et ses objectifs ne sont pas toujours directement reliés à des enjeux technologiques.
De nombreuses disciplines peuvent être regroupées sous cette dénomination diffuse dont :
|
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Mais JYG, évacue le recours à la topologie et à la nodologie ....(me semble-t-il !?). à documenter et préciser ... | ||||||||||||||||||||||||||||||||||||||||||||||
| Inertie | ✔ |
- voir Principe d'inertie, loi d'inertie, Force d'inertie, Ency d'Alembert , - Inertie, La force d'inertie, - Principes mathématiques de le philosophie naturelle, Newton, 1687 (pour le référentiel galiléen) - Histoire de l'inertie, D'Aristote à Einstein, Robert Signore, 2012, Vuibert, - Voir Langage, structure du langage, Langage et inertie, la structure du langage c'est le principe d'inertie |
||||||||||||||||||||||||||||||||||||||||||||
| Initiation | ✔ |
- La psychanalyse est une anti-initiation. L’initiation, c’est ce par quoi on s’élève, si je puis dire, au Phallus. C’est pas commode de savoir ce qui est initiation ou pas. Mais enfin l’orientation générale, c’est que le phallus, on l’intègre. Il faut bien qu’en l’absence d’initiation, on soit homme ou on soit femme. Bon...TT16011979, - Mode de transmission d'un savoir par des épreuves rituelles et sexuelles, marquant un changement d'état du sujet, et fédérant un groupe social. ( apprentissage de codes, attribution de signes distinctifs, de traits, révélation de symboles, d'un mythe et mise en relation avec les ancêtres ..) ...constitutifs de la loi de groupe. (voir Mauss.M) - De l'initiation avec CANTOR, |
||||||||||||||||||||||||||||||||||||||||||||
| Intégration, | ✔ |
-En mathématiques, l'intégration est le fait de calculer une intégrale. C'est aussi une des deux branches du calcul infinitésimal, appelée également calcul intégral, l'autre étant le calcul différentiel.
Les opérations de mesure de grandeurs (longueur d'une courbe, aire, volume, flux...) et de calcul de probabilités étant souvent soumises à des calculs d'intégrales, l'intégration est un outil scientifique fondamental1. C'est la raison pour laquelle l'intégration est souvent abordée dès l'enseignement secondaire. Les différents domaines dans lesquels peuvent se rencontrer des intégrales ont conduit à donner des définitions différentes de l'intégrale permettant d'en calculer pour des fonctions de moins en moins régulières. On rencontre ainsi les intégrales dites de Riemann, de Lebesgue ou de Kurzweil-Henstock. Mais toutes ces définitions coïncident dans le cas des fonctions continues. Le symbole mathématique représentant l'intégration, le « S long » : ∫ , ∫est appelé signe somme, signe d'intégration, signe intégral ou intégrateur ; il a été introduit par Leibniz pour noter l'intégrale. - des méthodes d'intégration approchées, sur Crhono Math, |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Intrinsèque↑
|
✔ | -
[En parlant d'un objet ou d'une pers.] Qui est inhérent, indépendamment de tous les facteurs extérieurs. - Interne ( Balay 1971 ). Nous entendons par propriétés intrinsèques et permanentes celles qui serviraient dans tous les cas, à la définition et à la construction des parties de la figure que nous avons appelées intégrantes ou principales ( Chasles , Aperçu, hist. orig. et développ. méth. géom., 1837 , p. 205). CNLRT, - Afin de préciser le narcissisme, JMV, 2007, Intrinsèque extrinsèque, la géométrie, la symétrie, la symétrie miroir, L'envers du narcissisme - Deux aspects géométriques du narcissisme, JMV 17 mai 2011 |
||||||||||||||||||||||||||||||||||||||||||||
Introjection ↑
|
✔ |
- couple introjection-projection - vient de Ferenczi et de M.Klein : bon ou mauvais objet introduit ou expulsé - L'introjection est symbolique (emprunt d'un trait signifiant, alors que la projection est imaginaire) (définitions empruntées au dictionnaire de la psychanalyse Larousse -hi !) : |
||||||||||||||||||||||||||||||||||||||||||||
| Invariant, | - - pour la topologie, la dimension, - pour la géométrie, pour le noeud, pour la psychanalyse, |
|||||||||||||||||||||||||||||||||||||||||||||
Involution signifiante ↑ |
✔ |
- C'est le rapport de la bande de Moebius et du tore dans l'Etourdit. Dans le Logique du fantasme du 5 ou 15 février 1967, il définit l'involution signifiante comme la copule qui unit l'identique et le différent, c'est la différence dans le phonème, la différence dans le rapport sexuel qu'il n'y a pas, dans le fait qu'il y a deux sexes et que c'est peut être le même (une seule libido masculine) mais aussi deux, celle du moi et celle de l'objet ! Nous travaillons avec deux libidos parce qu'on travaille sur le phonème, on travaille dans l'opposition. JMV 0906210 ENS - Le DI, la droite infinie, 2006, J-M.V - La métaphore du nom du père comme envers du narcissisme, JMV 2004, involution entre les formules de la sexuation et les tours du dit dans l'Etourdit |
||||||||||||||||||||||||||||||||||||||||||||
| Insensé | ✔ |
-un logicien de Louvain qui lui a parlé des insensés, il a introduit un nouveau type d’écriture que René Guitart a repéré en Logique justement, il y a les irrationnels des grecs, les imaginaires des classiques, et bien parlons maintenant après Boole et les magnifiques constructions des logiciens du XIX et du XX siècle, il dit parlons des insensés, et il dit que c’est toujours comme ça, ça parait insensé à première vue, parce qu’on a des préjugés, mais finalement, ça résout ...JMV23062015 | ||||||||||||||||||||||||||||||||||||||||||||
Isométrie ↑ |
✔ |
- les isométries permettant les changements de présentations d'un noeud s'effectuent selon les mouvements élémentaires de Reidemaster. Noeud ChapIVp123... - Dans le plan euclidien, on appelle symétrie axiale la symétrie orthogonale par rapport à une droite : le vecteur MM' est perpendiculaire à (d). Cette symétrie conserve les distances : il s'agit d'une isométrie . Les angles géométriques sont conservés mais elle change les angles orientés en leur opposé. On appelle isométrie toute application de E dans E conservant les distances. Chronomath , - Isométries du cube, - Deux aspects géométriques du narcissisme, JMV 17 mai 2011 - Isométries du tore : rotation, retournement, symétrie centrale, symétrie axiale, et composition d'une rotation et d'un retournement . - Dans l'espace euclidien, toute application de E dans E conservant les distances est une Isométrie pour A et B. ex : -le groupe orthogonal (ou rotations vectorielles), -la translation, -la symétrie axiale, - la symétrie centrale, -la réflexion, -la symétrie glissées, -la rotation dans le plan(sic), -le vissage ou déplacement hélicoïdal, Cronomath source, |
||||||||||||||||||||||||||||||||||||||||||||
| Isomorphisme, | ✔ |
- Se dit de deux ensembles en correspondance biunivoque (ou bijective), munis chacun d'une loi de composition interne, de telle façon que ces lois appliquées à des éléments correspondants donnent pour produit des éléments correspondants`` (Lar. encyclop.). Nos deux espaces se correspondent donc point à point : ils peuvent être « transformés » l'un dans l'autre : ils sont isomorphes (H. Poincaré, Valeur sc.,1905, p. 122).Klein découvre deux groupes isomorphes; l'un concernant le polyèdre régulier appelé icosaèdre, l'autre l'équation du cinquième degré (Gds cour. pensée math.,1948, p. 203). CNRTL, |
- W, |
|||||||||||||||||||||||||||||||||||||||||||
Isotopie↑ |
✔ |
- déformation continue d'un objet sans recoupement, Etoffe p 117, p 30 - l'isotopie est définie par les mouvements de Reidermaster. |
||||||||||||||||||||||||||||||||||||||||||||
| J | ||||||||||||||||||||||||||||||||||||||||||||||
| Jeux | - le jeu et la topologie, chap V, La description de la caverne, p157, Etoffe, JMV - Jeux divers, pour les quatre saisons , - Matériel en vue ... d'exercices pour assouplir ... au moins les doigts ... ! |
|||||||||||||||||||||||||||||||||||||||||||||
| K | ✔ |
Ka-Kl- |
||||||||||||||||||||||||||||||||||||||||||||
k |
✔ |
- Nombre de la coupure Kip = q - b , ( q et b correspondent aux croisements par où passe la coupure, pouvus ici de leur signe de torsion. Nous appellerons partie nouage cette espression (q - b ), c'est le nombre de la coupure. ( i pour orientation et p pour présentation) (J-M.V, Noeud p 104) |
||||||||||||||||||||||||||||||||||||||||||||
Kant |
- La logique de Kant,
in Bibliographie, - Critique de la Raison pure, Préface de la seconde édition, 1787, Texte ! philo-labo, 22 pages Traduction et analyse par Ole Hansen-Love, 2019, - l'idée de la critique transcendantale , c'est l'idée de la structure même du langage, en tant qu'il n'y a pas de métalangage, c'est qu'il y a du métalangage, mais cela n'en est pas, alors c'est difficile à comprendre pour un occidenté, c'est que le processus critique, la meilleur c'est celle de Kant, c'est la seule chose qu'on pourra retenir de Kant ! |
|||||||||||||||||||||||||||||||||||||||||||||
Kantiques (formules ); Kantification |
✔ |
- lecture des formlules kantiques de la sexuation (texte intégral), 2007, JMV (Saint Anselme ! divers arguments ontologiques (St Anselme, Descartes, Leibnitz, ...St Thomas...), .pdf, IFAC, |
||||||||||||||||||||||||||||||||||||||||||||
Kauffman L.H |
✔ |
- bio, - On Knots, (ouvrir dans un nouvel onglet) |
||||||||||||||||||||||||||||||||||||||||||||
| Klein | - Programme d'Erlangen, voir ci-dessus Erlangen, | |||||||||||||||||||||||||||||||||||||||||||||
Klein ( Bouteille de) |
✔ |
- la bouteille de Klein est associée à la voix dans l'analyse. Surfaces topologiques, - Les surfaces topologiques intrinsèques, - Surface topologique unilatère, |
||||||||||||||||||||||||||||||||||||||||||||
Klein (groupe de ) |
- Vievergruppe, est le pllus petit groupe non trivial qui ne soit pas cyclique. Il a quatre éléments et tous sauf l'élément neutre ont un ordre égal à 2 - sur wiki, ! |
|||||||||||||||||||||||||||||||||||||||||||||
| En mathématiques, le groupe de Klein, est, à isomorphisme près, l'un des deux groupes à quatre éléments, l'autre étant le groupe cyclique C4 ; c'est le plus petit groupe non cyclique. Il porte le nom du mathématicien allemand Felix Klein, qui en 1884 le désignait par « Vierergruppe » (groupe de quatre) dans son « cours sur l'icosaèdre et la résolution des équations du cinquième degré » | ||||||||||||||||||||||||||||||||||||||||||||||
| Les groupes, J.DIEUDONNÉ, EU, | W, |
|||||||||||||||||||||||||||||||||||||||||||||
| L | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
| LACAN et les mathématiques, | ✔ |
- Lacan et les mathématiques, JMV09022011, Rouen, - Parcours mathématique, |
||||||||||||||||||||||||||||||||||||||||||||
Lacan (noeud de ) |
✔ |
- 332252-442, noeud de Lacan, .pdf, |
||||||||||||||||||||||||||||||||||||||||||||
| Lambda calcul | ✔ |
- Le lambda-calcul (ou λ-calcul) est un système formel inventé par Alonzo Church dans les années 1930, qui fonde les concepts de fonction et d'application. On y manipule des expressions appelées λ-expressions, où la lettre grecque λ est utilisée pour lier une variable. Par exemple, si M est une λ-expression, λx.M est aussi une λ-expression et représente la fonction qui à x associe M.
Le λ-calcul a été le premier formalisme pour définir et caractériser les fonctions récursives : il a donc une grande importance dans la théorie de la calculabilité, à l'égal des machines de Turing1 et du modèle de Herbrand-Gödel. Il a depuis été appliqué comme langage de programmation théorique et comme métalangage pour la démonstration formelle assistée par ordinateur. Le lambda-calcul peut être typé ou non. Le lambda-calcul est apparenté à la logique combinatoire de Haskell Curry et se généralise dans les calculs de substitutions explicites. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Langage↑ |
✔ |
- Langage, langue, Lecture, parole et écriture *, |
||||||||||||||||||||||||||||||||||||||||||||
Langage des prédicat de premier ordre ↑ |
✔ | - voir calcul des prédicats, -L1T1, langage des prédicats, articulation dans le graphe, (Langage Théorie) - lecture des formules kantiques de la sexuation (texte intégral simplifié), 2009, JMV articulatio dans le graphe |
||||||||||||||||||||||||||||||||||||||||||||
Langage des prédicat
de premier ordre monadique↑ |
✔ | - Chaque symbole de prédicat a une arité qui détermine le nombre d'argument ou d'objet auquel il est appliqué. Dans : ses yeux sont bleus, le prédicat bleux a une arité d'un, on dit qu'il est monadique ou unaire -L1T1mon, |
||||||||||||||||||||||||||||||||||||||||||||
Langage des propositions ↑ |
✔ | - Calcul des propositions, (logique stoïcienne), -L2T2, langage des propositions ou calcul de la coordination, articulation dans le graphe, (Langage Théorie) - La LCC, in L'amour du tout aujourd'hui, 2 eme partie, JMV, 1992 - lecture des formules kantiques de la sexuation (texte intégral simplifié), 2009, JMV |
||||||||||||||||||||||||||||||||||||||||||||
| LT ST |
✔ | Langage, (Langue); Théorie, Système d'écriture, Syntaxe; Théorie, |
F, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
| Mathématiques, Topolgie générale, Topologie ensembliste, |
- Les mathématiques se distinguent des autres sciences par un rapport particulier au réel car l'observation et l'expérience ne s'y portent pas sur des objets physiques ; les mathématiques ne sont pas une science empirique. | |||||||||||||||||||||||||||||||||||||||||||||
| L0T0 (L0T0) S0T0 (S0T0) |
Théorie des ensembles, Pcs, |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
| L1T1 S1T1 |
✔ |
Calcul des prédicats, Quantification, Fonctions propositionnelles...Concepts... connecteurs logiques (∧, ET; ∨, OU) , deux quantificateurs logiques : l'un universel ∀( pour tout) et l'autre existentiel ∃(il existe) . |
||||||||||||||||||||||||||||||||||||||||||||
| L2T2 S2T2 |
✔ | Calcul des propositions, calcul propositionnel, calcul des énoncés, calcul de la coordination, Vérification et vérifonctionnalité, V-F, 1,0; Algèbre de Boole, |
↑ | |||||||||||||||||||||||||||||||||||||||||||
| L3T3 S3T3 |
✔ | Topologie du sujet, Logique modifiée, Négation modifiée, Premier, |
||||||||||||||||||||||||||||||||||||||||||||
Effectivité |
✔ | Entre Cs et P, (Conscience et Perception) , ente m.i et M.I, - c'est l'enchainement (JMV020914-39.42), .htm, , planche, .swf, - un discours qui se tient, qui est enchainé, c’est là que la notion de chaine va apparaître en tant qu’elle représente l’effectivité, Substituer l'Effectivité à la Réalité ...! |
||||||||||||||||||||||||||||||||||||||||||||
développement ci-dessous |
||||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
| LT ST |
✔ | Langage, (Langue); Théorie, Les systèmes d'écriture sont des Langage symboliques (Carnap), ou langues formulaire (Frege et Claude Imbert) qui s'opposent à la Phénoménologie, et aux USA c'est devenu les Systèmes formels. (voir Système d'écriture). |
||||||||||||||||||||||||||||||||||||||||||||
Mathématiques, faire des mathématiques, Topologie Générale, ou Topologie ensembliste, |
✔ | -Les mathématiques se distinguent des autres sciences par un rapport particulier au réel car l'observation et l'expérience ne s'y portent pas sur des objets physiques ; les mathématiques ne sont pas une science empirique. Elles sont de nature entièrement intellectuelle, fondées sur des axiomes déclarés vrais ou sur des postulats provisoirement admis. Ces axiomes en constituent les fondements et ne dépendent donc d'aucune autre proposition. - Faire des mathématiques, résoudre un problème, par différentes voies, se tromper, ..... - Les mathématiques (ou la mathématique) sont un ensemble de connaissances abstraites résultant de raisonnements logiques appliqués à des objets divers tels que les ensembles mathématiques, les nombres, les formes, les structures, les transformations, etc. ; ainsi qu'aux relations et opérations mathématiques qui existent entre ces objets. Elles sont aussi le domaine de recherche développant ces connaissances, ainsi que la discipline qui les enseigne. Elles possèdent plusieurs branches telles que : l'arithmétique, l'algèbre, l'analyse, la géométrie, la logique mathématique, etc. Il existe également une certaine séparation entre les mathématiques pures et les mathématiques appliquées. - Topologie générale, TG, Théorie des catégories, Cs, m...i, Secondaire, Symboles; , - Avec pour antécédent historique La Syllogistique d'Aristote, La Logique mathématique moderne est un des piliers des Mathématiques, - vous avez pour les structures algébrique : |
|
|||||||||||||||||||||||||||||||||||||||||||
| Les catégories Langage, Syntaxe ou Systèmes d"écriture, Théorie sont indiciées, elles ne le sont souvent pas par ....paresse ! | ||||||||||||||||||||||||||||||||||||||||||||||
| L0T0 S0T0 |
Théorie des ensembles, Pcs, - voir Ensemble, ci-dessus, - voir Théorie des ensembles ci-dessous, - Une collection est un ensemble et les ensembles sont des assemblages, ils ne représentent pas, ils sont ! Qu’est-ce qu’un ensemble ? Une multiplicité d’éléments, une collection, une classe, mais en Théorie des ensembles il apparait que n’importe quelle multiplicité n’est pas un ensemble (Paradoxe du coiffeur de Russel : ensemble des ensembles qui ne se contiennent pas eux-mêmes), soit une Classe ! Théorie des ensembles, J-M.VAPPEREAU, 10-09-2013, |
F, |
||||||||||||||||||||||||||||||||||||||||||||
| L1T1 S1T1 |
✔ |
Calcul des prédicats, Quantification, Ics, - voir la Logique d'Aristote, antécédents hisoriques, du Calcul des prédicats; lire les Textes d'Aristote sur gaogoa, |
Math et schema L, L1, L2, F, .swf, |
|||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
| L2T2 S2T2 |
✔ | Calcul des propositions, calcul propositionnel,
La logique stoïcienne (W) qui se prolonge dans une partie du Calcul des propositions, est un autre pilier des mathématiques. |
↑ | |||||||||||||||||||||||||||||||||||||||||||
| L3T3 S3T3 |
✔ | Topologie du sujet, Logique modifiée, Négation modifiée, Premier, |
F, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
| La Logique modifiée est une logique construite d'une manière linéaire sur une Algèbre de Boole.voir JMV juin 2015, Algèbre de Boole , est de caractéristique 2 (0,1); qui a pour éléments 2 puissance n, pour 2 : (00, 01, 10, 11); pour 3 : (000, 001, 010, 011, 100, 101, 110, 111); C'est une extention des dimensions de la LCC. |
Math et schema L, L1, L2, F, .swf, |
|||||||||||||||||||||||||||||||||||||||||||||
Le plongement de la logique classique dans la logique modifiée permet de former, d'écrire, côté femme, |
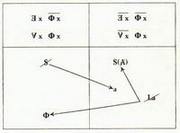 |
|||||||||||||||||||||||||||||||||||||||||||||
Effectivité |
✔ | Entre Cs et P, (Conscience et Perception) , ente m.i et M.I, | ↑ | |||||||||||||||||||||||||||||||||||||||||||
| - c'est l'enchainement (JMV020914-39.42), .htm, , planche, .swf, - un discours qui se tient, qui est enchainé, c’est là que la notion de chaine va apparaître en tant qu’elle représente l’effectivité, de quelque chose d’effectif, qui tient, quand on tire dessus dans tous les sens, ça tient, et c’est ça qui fait, c’est ce que moi j’appelle effectivité, et que j’oppose à la réalité qu’on voudrait nous imposer, surtout de plus en plus, du fait, c’est pas seulement du fait de l’influence du Cercle de Vienne, et du logico positivisme, même avant Russel, il faisait déjà du logico-positivisme, Bertrand Russell, donc la question de l’effectivité, en allemand, au début des Ecrits, vous verrez ça, Lacan en parle dans ses antécédents, il souligne cette différence chez Freud entre Realitad et Virtsgeigt et le virlitsgeit, c’est deux manière de parler de la réalité, et Virtgeigt, il y en a une qui s’appelle effectivité, je propose de le traduire par effectivité, si on fait quelque chose effectivement, peut être y-a-t-il du mensonge, mais pourquoi le mensonge ne serait pas lui-même effectif, le mensonge c’est bien lié au fait de dire, et ça a une effectivité le fait de dire, c’est même la fonction phallique, par excellence, JMV23062015 |
F, |
|||||||||||||||||||||||||||||||||||||||||||||
Langue ↑ |
✔ |
- Il y a des langues, la langue, et si Lacan dit que " l'inconscient est structuré comme un langage", c'est plus pour le joke, le jeu de mot "commun langage" qu'il le dit, - langue, langage, parole, - Il ne faut pas beaucoup s'intéresser à la pensée, plutôt à la langue. JMV27012015, et Langue |
||||||||||||||||||||||||||||||||||||||||||||
| Languene (la ou le, selon le contexte) |
✔ | - La languene, 2, (le mur des formants), en langue noeuds , le Phare des lacans, mais p-ê..fard !? (en suédois far est le père !). - Parler Le Languene, c-à-d se débrouiller avec ce matériel, ... du Tricot au 3 Bo, en passant par ...boboland.... - Système d'écriture : dessins et commentaires, - voir PIANOEUDS, - voir Treillis, |
||||||||||||||||||||||||||||||||||||||||||||
langue auxiliaire ↑ |
- entre proposition et concept, et ils vont découvrir la nécessité du métalangage, révélée par Jakobson, dans la Linguisitique, mais qui déjà se trouve chez Frege sous le nom de langue auxiliaire, à côté des langues formulaires JMV22062010, nécessité d'une langue auxiliaire pour le commentaire, c'est la formule de Frege, le mot de métalangage ne viendra que plus tard, et chez Boole ça s'appelle la différence entre les énoncés primaires et les énoncés secondaires, il y a des énoncés qui traitent des énoncés primaires, et alors il faut réduire les primaires au calcul des proposition, d'où ce nom, mais le même calcul se produit pour les concepts et les deux sont mélangés | |||||||||||||||||||||||||||||||||||||||||||||
langue formulaire ↑ |
✔ | - ? - Langage des théorèmes de la géométrie, différent de la prose et de la poésie (L'Iliade et l'Odyssée), fixe le goût pour la formule, mémorisable, pérenne, vrais ... |
||||||||||||||||||||||||||||||||||||||||||||
Lattices
|
✔ |
- voir Treillis | ||||||||||||||||||||||||||||||||||||||||||||
Lecture↑
|
✔ | - origine divinatoire de l'écriture chinoise, - destruction de la lecture dans la psychose commune. - Lecture des formules de la sexuation, voir Sexuation - Tout le monde à partir du narcissime et du trauma, a des difficutlé avec la lisibilité, - Le corps écrit, et entre le Symbolique et l'écriture d'une langue, il se produit de la lisibilité, une lecture.. - Lecture puis écriture ... - voir Lire, Lisiblilité , Massacre, Paranoïa, - la lecture précède l'écriture, JMV20150602, p16 |
||||||||||||||||||||||||||||||||||||||||||||
Lemme ↑ |
✔ | Le lemme , en mathématiques et en logique mathématique , est un résultat intermédiaire sur lequel on s'appuie pour conduire la démonstration d'un théorème plus important. Dans l'Antiquité grecque, lemme (en grec ancien : λῆμμα) était un terme de logique : il désignait la majeure du syllogisme, c'est-à-dire la première assertion. Dans la dialectique grecque, le lemme, le prolemme et l'épiphore sont les trois parties de l'argument. Par extension, lemme désigne en mathématiques l'un des arguments de la preuve sans en être le fondement puis, plus généralement, un résultat intermédiaire utile à la démonstration d'un théorème. - se sont des résultats en général très court, dont la preuve est courte également, qui seront utilisé dans la preuve plus importante d’un théorème.
|
W, |
|||||||||||||||||||||||||||||||||||||||||||
Lemme de Dehn ↑ |
✔ | En mathématiques, le lemme de Dehn est un résultat de topologie des variétés de dimension trois. Il énonce que l'existence d'une fonction affine par morceaux d'un disque vers une variété de dimension 3, dont les points singuliers se trouvent dans l'intérieur du disque, implique l'existence d'une autre fonction affine par morceaux entre ces espaces, qui est un plongement et qui est identique à l'originale sur les bords du disque. On pensait ce théorème démontré par Max Dehn en 1910, mais une erreur a été trouvée dans la démonstration par Hellmuth Kneser. Le statut du lemme de Dehn est demeuré incertain jusqu'en 1956. Il a été prouvé à cette date par Christos Papakyriakopoulos en utilisant une construction ingénieuse à base de revêtements. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Lettre ↑ |
✔ | -La lettre c'est le produit de la rupture de semblant et c'est des morceaux de signifiant, le signifiant quand il est rompu, il tombe en petits bouts et ça donne des lettres.( JMV 9-06-10 ENS) - La lettre est une des deux réalisations du phonème, avec le signifiant, - voir Ecriture origine divinatoire de l'écriture chinoise, - L'instance de la lettre dans l'inconscient ou la raison depuis Freud, E493, 1957, ttymupt...tjrs trop tard ! - on fabrique des Lettres et des Noms propres avec des restes de discours tombés en désuétude - un problème qui apparait dans l’écriture, qui se formule, qui se construit, qui s’écrit, et qui n’a pas toujours des solutions, et des fois il faut ajouter des lettres pour trouver des solutions à des problèmes qui n’en ont pas sans ça ! ( voir Mathématique) - L’écriture Introduit la discontinuité dans le continu, hors il se trouve que ça fonctionne très bien avec le phonème, qui est d’abord parlé, ce que Lacan appelle le Signifiant, et moi je vous propose de parler du phonème dans la psychanalyse avec Lacan en terme de Signifiant pour ce qui est du côté des oreilles, dans ce qui s’entend, et de parler du phonème dans ce qui s’écrit et qui s’appelle la Lettre chez Lacan, vous avez ça dans l’Instance de la lettre, Lacan parle, au moment ou Lacan introduit l’algorithme Saussurien, le S/s, il parle de la chaine signifiante et il dit, et il parle de l’élément différentiel dernier qui est la Lettre et qu’on appelle phonème, !!, alors voyez là, il emploie le mot phonème pour la lettre ! et même le mot phonème pour le lettre et le mot lettre pour le phonème, donc moi je pense que le phonème des linguistes, il y a le phonème dans la langue parlée, du locuteur, dans la langue vulgaire, dans la langue de celui qui parle de manière plus ou moins continue, dans le flux verbal qu’on ne comprend pas si on ne le découpe soit même, donc écouter quelqu’un ou lire, c’est découper, c’est introduire ce que Freud appelait dès les Etudes sur l’aphasie, les verneinugzeichen, voyez dans les schémas de Freud, vous avez Verneinung et Verneinungzeichen, vous avez perception et perception-signe, JMV16062015 |
||||||||||||||||||||||||||||||||||||||||||||
Lettre 52 ↑
|
✔ | - La lettre 52, in La naissance de la psychanalyse, lettre 52 du 06121896, page 154, fig 7(2), Freud,Puf - Graphe de la lettre 52, Freud - Pliage du graphe de la lettre 52, par Lacan puis par J-M.Vappereau - L52 au schema L, - Lettre 52 & Schema L, complete |
||||||||||||||||||||||||||||||||||||||||||||
Lettre volée |
✔ | - Le séminaire sur " la Lettre volée", 1956, Ecrits p11, Lacan, [ dont Présentation de la suite ( schéma L); Parenthèse des parenthèses, (réseau α β)1966. ] - Séminaire sur la Lettre volée, (version Elp), (version Staferla); J.Lacan - la lettre volée, (htm), (.pdf), E.Poe (Dans Histoire extraordinaires, traduit par Baudelaire) |
||||||||||||||||||||||||||||||||||||||||||||
Libido ↑
|
✔ | - la surface de l'étoffe (ou quotient du groupe fondamental –Essaim, chap I, p 60), est identifiée à la libido, (E a 30, p846). |
||||||||||||||||||||||||||||||||||||||||||||
Lickorish, W.B.Raymond |
✔ | - Lickorish est un grand algébriste, j’admire Lickorish comme algébriste, c’est lui qui a écrit l’introduction au nouveau livre sur la Théorie des nœuds, très beau livre, de chez Springer, avant c’était le Fox & Crowel, ( en fait le livre de Lickorish se nomme Introduction to Knot Theory, (Sommaire) by W.B.Raymond Lickorish); ( peut être commandé à la librairie Eyrolles, au même prix que chez Verlag en vertu d’un accord Verlag/Eyrolles), le Fox & Cowell qui traitait juste des groupes, Lickorish il a mis son nez là dedans, c’est une type en Californie qui travaille, qui a beaucoup de relations avec Kauffmann, de Chicago, en Théorie des noeuds, moi ( J- M.Vappereau), je ne suis pas du tout de l’avis de faire les mêmes choses qu’eux, et de remplacer le problème topologique des nœuds par un problème algébrique classique, ils essaient de remplacer les nœuds par des polynômes, mais quand je lis Lickorish dans ses exercices d’algèbre, même quand il traite des nœuds, je reconnais que c’est un grand algébriste, et je trouve ça magnifique, je pense qu’on peut rentrer là dedans, c’est pas être un calculateur prodige (JMV23092014, 1.05.05).(.html) - |
W, En |
|||||||||||||||||||||||||||||||||||||||||||
Ligne, |
✔ |
- & dimensions, - comme ensemble de points, (.swf), |
||||||||||||||||||||||||||||||||||||||||||||
Limite |
✔ | - En analyse mathématique, la notion de limite décrit l’approximation des valeurs d'une suite lorsque l'indice tend vers l’infini, ou d'une fonction lorsque la variable se rapproche d’un point (éventuellement infini) au bord du domaine de définition. Si une telle limite existe dans l’ensemble d’arrivée, on dit que la suite ou la fonction est convergente (au point étudié). Si ce n’est pas le cas, elle est divergente, comme dans le cas de suites et fonctions périodiques non constantes (telle la fonction sinus en +∞). - Si les valeurs successivement attribuées à une variable s'approchent indéfiniment d'une valeur fixe, de manière à finir par en différer aussi peu que l'on voudra, alors cette dernière est appelée la limite de toutes les autres. (Cauchy, Résumé des leçons sur le calcul infinitésimal, site Melh) - Applications linéaires, Fonctions algèbriques, Suites numériques, |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Linéarisation | ✔ | - en géométrie, le fait de trouver la ligne ayant la même longueur qu'une courbe, par exemple déterminer le périmètre d'une figure ; la linéarisation du cercle revient à déterminer le nombre pi (voir aussi Quadrature du cercle pour ce qui est du carré ayant la même aire qu'un disque) ; - autres définitions sur wikipedia, : en analyse, en trigonométrie, en théorie des langages formels, en informatique, |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Linguisterie
|
✔ | - Néologisme de Lacan pour désigner le langage de l'inconscient de Freud et le différencier de la linguistique de Jakobson. (Encore, 19121972) (Télévision, AE,p511) (la troisième, 01111974) (L'insu que sait, 15031977) . - Langage, |
||||||||||||||||||||||||||||||||||||||||||||
Linguistique↑ |
✔ | - Il n'y a pas de linguistique . - L'étude la linguistique doit surmonter les deux épreuves de son enterrement en grandes pompes ! La première due à Chomsky (1, 2) qui reprend les grammaires chomskyennes de Carnap, ( Structure syntaxiques et théorie des traces, puis gouvernement et liage ! ) et stope net les recherches en linguistique, ce qu'il viendra marteler pour les sourds au Collège de France (entre autre) du 28 au 31 mai 2010. (voir CHOMSKY) et la seconde épreuve (l'à Mort du Signe), du côté de chez Saussure, qui revient à la représentation du Signe Saussurien, entre Signifiant et signifié, alors qu'il faudrait revenir au PHONEME découvert par Baudouin de Courtenay, or c'est pas le signal qui compte, pas la phonétique, mais le son, le signifiant, ça se passe du côté des oreilles. Il faut se tourner vers la phonologie, du côté de chez Troubetskoï, et ses "Principes de phonologie". (à préciser, à développer) . - à propos du Signe, vital et non humain, JMV20110201_01, page 11, 350 - Voir Langage & Langage et linguisitique; & Lexique, - Le langage est la condition de l'inconscient, et l'inconscient est la condition de la linguistique, s'il n'y a pas de lecture de l'inconscient, il n'y a pas de linguistique.JMV23062015 - L'inconscient est une linguistique fantastique. - La linguistique est l'étude scientifique du langage humain. (1) Le français `standard' ou le français `normatif' ne représente qu'une très petite tranche du français. Tout un ensemble de dimensions viennent compliquer ce tableau. Comme toute autre langue, le français varie selon la région, l'âge, le sexe, le niveau d'instruction des locuteurs, le registre, le genre, la situation et le médium (langue orale ou langue écrite), pour ne nommer que ces facteurs. En même temps, une langue se renouvelle constamment, au moyen de créations internes et d'emprunts à d'autres langues. La grammaire normative d'une langue fixe des principes pour la communication écrite soignée, mais n'a pas beaucoup à dire sur les autres variétés. Pour le faire, la linguistique se sert de l'approche descriptive , qui consiste à relever et à décrire les variations d'usage dans une communauté, sans porter de jugements a priori sur leur acceptabilité. - Linguistique, - Linguistique ( cours), - les écoles et courants, - Saussure ( école française), Jakobson, Troubetzkoï (école de Pragues), Hjelmslev (cercle de Copenhague), Hintikka, Chomsky ( Ecole anglaise, Yales) , Derrida, Fontanier, Martinet, Milner, Ducrot, Paulhan, Benneveniste, Parrain, Barthes ( Ecole française) [ Kripke ≠ Wittgenstein, Peirce, Quine, Carnap, Tarski.. à classer] |
||||||||||||||||||||||||||||||||||||||||||||
Lire |
✔ |
- Lire c'est une exercice qui se pratique à partir du narcissisme, et c'est difficilie pour tout le monde. |
|
|||||||||||||||||||||||||||||||||||||||||||
Lisibilité |
✔ |
- voir Lecture, voir Lire | ||||||||||||||||||||||||||||||||||||||||||||
Listing |
✔ |
- Introduction à la topologie, flip book - Thèse de Listing, .pdf, Etude préliminaire à la topologie, par Johann Benedict LISTING, traduit de l'allemand par Claude LEGER et Machael TURNHEIM, |
||||||||||||||||||||||||||||||||||||||||||||
Listing (famille des) ↑ |
✔ |
Les nœuds propres et impropres se répartissent en deux familles dites Trèfles et Listing Np81 |
||||||||||||||||||||||||||||||||||||||||||||
Logiques ↑ |
✔ |
- s'exercer, faire des exercices de Logique, et de Mathématique : récréomath, Textes et sites, ... - Le calcul de la coordination met l'accent sur les connecteurs logiques (OU, ET), leurs fonctions, plutôt que sur les objets, les lettres, comme dans le calcul des propositions qu'on devrait plutôt nommer calcul des énoncés (Rivenc et Vappereau) car portant sur des propositions ET des concepts ! -JMV22062010 ENS, L56- La Logique ne peut pas être écrite, décrite à partir de la Théorie des ensembles, c'est l'inverse ! La théorie des ensembles peut être écrite grâce à la Logique ! |
||||||||||||||||||||||||||||||||||||||||||||
Logique de Boole ↑ |
✔ |
-voir Boole - Logique de Boole, - Algèbre de Boole, - Axiome de Boole, voir Axiome de Boole 2, , - Algèbre de Boole et Logique modifiée, |
||||||||||||||||||||||||||||||||||||||||||||
Logique classique |
✔ |
- J’ai des craies, alors là je mets dans un rond des craies bleues, là je mets dans un rond les craies rouges, là les craies vertes, et ya pas d’intersection, yen a pas qui sont dans les deux ronds en même temps, c’est disjoint, c’est une partition ça s’appelle en math, 25 :54, là avec les craies blanches un autre rond, voyez je fais des petits ronds autour pour qu’ils soient bien séparés, ça s’appelle classification, c’est pour ça que ça s’appelle logique classique, la logique classique classifie, - La Logique classique est moebienne, ce qui veut dire qu'elle correspond à des surfaces qui n'ont qu'une seule face, alors que la Logique modifié est bilatère, soit des surfaces à deux faces distinctes. |
||||||||||||||||||||||||||||||||||||||||||||
Logique canonique classique L2T2 |
✔ |
La Logique canonique classique, est l'agencement de la théorie de la vérifonctionnalité et de la théorie de la kantification, désormais (LCC). - Plaçons-nous en Langage des prédicats du premier ordre, c’est à dire que nous admettons et considérons connu le Calcul des propositions, soit la théorie de la vérifonctionnalité qui régit la coordination grammaticale entre concepts et entre propositions.
- Logique classique, sur Wiki, Aristote, Le dérapage d'Aristote, par J-M.VAPPEREAU, - J’ai des craies, alors là je mets dans un rond des craies bleues, là je mets dans un rond les craies rouges, là les craies vertes, et ya pas d’intersection, yen a pas qui sont dans les deux ronds en même temps, c’est disjoint, c’est une partition ça s’appelle en math, 25 :54, là avec les craies blanches un autre rond, voyez je fais des petits ronds autour pour qu’ils soient bien séparés, ça s’appelle classification, c’est pour ça que ça s’appelle logique classique, la logique classique classifie, |
||||||||||||||||||||||||||||||||||||||||||||
| Logique déductive et logique inductive ↑ |
✔ |
- La déduction est une opération par laquelle on établit au moyen de prémisses une conclusion qui en est la conséquence nécessaire, en vertu de règles d'inférence logiques. Ces règles sont notamment l'objet des Premiers Analytiques d'Aristote. On va des causes au effets, des principes aux conséquences, du général au particulier . La conclusion est aussi certaine que les prémisses. Le Syllogisme est la principale forme de la déduction. Le syllogisme peut devenir un raisonnement fallacieux, c'est le sophisme, ! On l'oppose généralement à l'induction, qui consiste au contraire à extraire d'un nombre fini de propositions données par l'observation, une conclusion ou un petit nombre de conclusions plus générales. Du particulier au général, mais danger du fait de la partialité des observations initiales, une preuve contraire peut renfre les conclusions de l'induction fausse. - Prolongement scientifique sur les Systèmes de pensée ....Daniel KAHNEMAN, !? - L'amour du tout aujourd'hui, 1ere partie , la fonction phallique, Cs et Ics avec Wundt, Tarski, le prédicat de Vérité, logique inductive et déductive |
||||||||||||||||||||||||||||||||||||||||||||
| Logique déontique, ( c'est une logique modale d'obligation) |
✔ |
La logique déontique gère les permissions, - La logique déontique standard est une formalisation mathématique de concepts philosophiques. Le choix de s'appuyer sur la logique modale normale présente des avantages calculatoires notables, mais engendre des incohérences et des paradoxes d'un point de vue philosophique, qui sont les principales critiques adressées à la logique déontique standard. Parmi les plus importants, on peut citer : - La logique déontique (du grec déon, déontos : devoir, ce qu'il faut, ce qui convient) tente de formaliser les rapports qui existent entre les quatre caractéristiques d'une loi : l'obligation, l'interdiction, la permission et le facultatif. Gottfried Wilheim Leibniz en 16701 proposa le premier d'appliquer la logique modale à la morale en remarquant l'analogie suivante : « l'obligatoire (modalité déontique) est ce qu'il est nécessaire (modalité aléthique) que fasse l'homme bon ». Il proposa la correspondante suivante :
Elle s'est développée à partir des années 1950 grâce aux travaux du philosophe finlandais Georg Henrik von Wright (Deontic Logic 1951)2. Reprenant la correspondance notée par Leibniz, il les formalise grâce aux avancées de la logique modale. Les progrès de la sémantique, et notamment la sémantique des mondes possibles ont encouragé le développement de la logique déontique. Comme pour chaque système logique aujourd'hui, il est erroné de parler DU système de la logique déontique. Il existe une grande variété de systèmes logiques déontiques, qu'on identifie selon les axiomes qu'ils intègrent — et toujours par référence à la logique modale générale. Lorsque l'on parle de logique déontique en général, on entend souvent le système classique et minimal, celui qui utilise les deux opérateurs de l'obligation (aux propriétés calquées sur celui de la nécessité) et de la permission (idem pour la possibilité), et de simples constantes et variables propositionnelles représentant des actions et / ou des états de choses (A, B, etc.). Mais la réalité déontique est multiforme : on peut interdire un état de choses, une action de la part d'un individu déterminé, un type d'action, etc. Elle nécessite donc plusieurs systèmes de logique déontique différents. Désormais, un système de logique déontique inclut le plus souvent aussi des notations pour représenter l'action et les individus (opérateurs d'action tels que STIT), et les recherches tendent à une complexification toujours croissante : intégration de la dimension temporelle grâce à l'indexation temporelle des propositions3, notion de trivalence, et autres. La logique déontique est à l'origine des systèmes normatifs, qui permettent de modéliser les obligations, les violations et les sanctions dans une organisation, et notamment dans un système multi-agents. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Logique du concept | - la logique classique classifie, Et c’est ça le concept, la logique du concept, JMV20110125, | |||||||||||||||||||||||||||||||||||||||||||||
| Logique du fantasme | ✔ |
- - Structure logique du fantasme, JMV 15 janvier 2014, ENS, |
↑ | |||||||||||||||||||||||||||||||||||||||||||
| - La logique du fantasme et sa topologie, JMV 24082014 - Le vel de l'aliénation, ..., JMV - Alénation séparation, - La logique c'est le fantasme (aliénation, séparation), - La logique du fantasme, Séminaire XIV, 1966-1967 - - la logique du fantasme et sa logique dans le diagramme d'Euler-Venn de quatre ronds, JMV 24082014 |
||||||||||||||||||||||||||||||||||||||||||||||
Logique formelle ↑ |
✔ |
- Logique mathématique ( Péano) ou Logique formelle (Frege-Church) ou Logique Méta-mathématique (Hilbert) o-,u Logique symbolique (/ à la Logique philosophique) ou Idéographie (Frege) [ comprennent : 6 théories des ensembles, L0T0,- Primitive; ZFC; la TGénérale Tarski Grotendick; la Théorie Newman Bernay; la théorie Morse kelley, la théorie Kripke Platek- ; la théorie de la Démonstration, la théorie des Modèles, la théorie de la Calculabilité (théorie de la Démonstration ?, théorie des Relations, théorie des Classes (Boole ou-et théorie des Ensembles NGB ?), théorie de la Coordination, Axiomatique )] - La logique formelle - c'est le système de la coordination, plus le calcul des prédicats de premier ordre kantifié (avec un k), c'est le noyau de la logique formelle, pour la science, depuis Frege, et les calculs de Boole s'inscrivent là dedans. JMV22062010, L177, L1142 |
||||||||||||||||||||||||||||||||||||||||||||
| Logique intuitionniste | ✔ |
- La logique intuitionniste est une logique qui diffère de la logique classique par le fait que la notion de vérité est remplacée par la notion de preuve constructive. Une proposition telle que « la constante d'Euler-Mascheroni est rationnelle ou la constante d'Euler-Mascheroni n'est pas rationnelle » n'est pas démontrée de manière constructive (intuitionniste)1 dans le cadre de nos connaissances mathématiques actuelles; car la tautologie classique « P ou non P » (tiers exclu) n'appartient pas à la logique intuitionniste. La logique intuitionniste établit, entre autres, un distinguo entre « être vrai » et « ne pas être faux » (formulation plus faible) car ¬¬P → P n'est pas non plus démontrable en logique intuitionniste. | ||||||||||||||||||||||||||||||||||||||||||||
Logique de Lacan ↑ |
✔ |
- C'est une logique qui se développe dans une Topologie des variétés, dite aussi la Topologie des espaces linéaires par morceaux (Piece-wiece topology) qui est une catégorie du sens de la théorie des Catégories de Birkhoff et MacLaine ou de Ehresmann.... Logique hyper triviale, et hyper simple ...mais très difficile du fait de son évidence ....p19, in Le vel de l'aliénation, JM-Vappereau, B-A,juillet 2006, - Une grande logique que Lacan entreprend de construire , selon Kaufman.(p19), à la façon de Hegel... - " C'est la version la plus délicate pour les lecteurs peu versés dans la pratique de l'algèbre, mais la plus intéressante pour se former à cette mathématique dialectique introduite par Lacan depuis les années cinquante dont aucun auditeur ne s'est inquiété semble-t-il, pour écouter Lacan, ni aucun lecteur depuis lors pour le lire enfin. A l'exception peut-être de Pierre Kaufman qui suggère, dans sa lecture donnée dans l'Encyclopédie Universalis, du texte que Freud à consacré à "La construction en analyse", que Lacan entreprend de construire ce qu'il appelle dans sa langue de professeur de philosophie: "une grande Logique" évoquant Hegel à cette occasion. Nous considérons pour notre part qu'il s'agit bien d'une Logique qui se développe en une Topologie des variétés, dite aussi la Topologie des espaces linéaires par morceaux (Piece-wiece linear topology) qui est une catégorie au sens de la théorie des Catégories de Birkhoff et MacLaine ou de Ehresmann. Lacan à construit lentement, avec patience, au travers d'une succession de marches peaufinées avec attention pour son séminaire et fabriquée avec soin, cette formidable Logique hyper triviale, hyper simple si nous la comparons aux travaux des logiciens mathématiciens du siècle vingt, mais précisément très difficile du fait de son évidence pour le sujet qui veut la pratiquer dans son effectivité." in Le velle de la séparation, p19 ! , B-A, P, 09-2009, - Le temps logique : le temps pour voir, le temps pour comprendre, le temps pour conclure. in - Le temps logique et l'assertion de certitude anticipée, un nouveau sophisme, Ecrits p197, Lacan, - Langage, mathématiques et topologie, - voir Temps |
||||||||||||||||||||||||||||||||||||||||||||
Logique mathématique ↑
|
✔ |
- Voir Logique
|
||||||||||||||||||||||||||||||||||||||||||||
| Logique et/ou Mathématique, | - , JMV20110125, page 17, ligne 566, | |||||||||||||||||||||||||||||||||||||||||||||
logique modale ↑ |
✔ |
- Système de logique qui comporte, en sus des connecteurs et quantificateurs de la logique classique, deux opérateurs unaires de modalité, l'un pour la nécessité (« il est nécessaire que… »), l'autre pour la possibilité (« il est possible que… »). Elle spécifie la qualité du Vrai ! voir wiki, nécessaire : La logique modale est une extension de la logique classique. Elle remonte à Aristote ; mais, après les travaux de Frege et de Russell qui ont montré sa nécessité par rapport à la logique classique, qui est binaire, Lewis a proposé une nouvelle formalisation, notamment par une axiomatisation du calcul propositionnel modal (1918). Quine a contesté à la fois la nécessité d'établir une logique modale et la possibilité même de cette démarche : mais la formulation des lois physiques montre que les scientifiques en font un abondant usage, à l'égard duquel les logiciens ne peuvent rester indifférents. C'est ainsi que la sémantique des logiques modales s'est notamment développée avec Kripke (1963) et surtout Hintikka (1969). (Larousse Encyclopédique) + - cours Papini, - Modalités, Euler-Venn, syllogisme et carré logique, (re_voir les modalité ici 1, 2, 3, ), - Clef pour la passe, 1ere partie, argument 3, dans L'amour du tout, JMV , aspect modal de la LCC de la coordination |
||||||||||||||||||||||||||||||||||||||||||||
Logique modifiée ↑ |
✔ |
- La Logique modifiée est bilatère, et conrrespond donc à des surfaces à deux faces distinctes, alors que la Logique classique est moebienne, JMV27012015 - Freud invente la cure analytique pour donner un lieu d'émergence et de symbolisation de la Logique modifiée, celle du rêve, des structures freudiennes du symptôme. Cette logique (modifiée) s'efface, s'évanouit, dans sa rencontre avec la Logique classique ( c'est l'oubli des rêves..) voir JMV20150602 p36 - la logique est modifiée dans la mesure ou elle est étendue à des dimensions plus grande, JMV20150602 - Algèbre de Boole et Logique Modifiée; - Eléments formels pour la logique modifiée, JMV - la différence s'efface dans l'identité, ....(JMV09092014, 01.09.42) - L3T3, Logique modifiée, (mise en supsens de la fonction phallique, logique asphérique. (Langage Théorie) - La LCC, in L'amour du tout aujourd'hui, 2 eme partie, JMV, 1992 - L'amour du tout, JMV, 1992, Elements formels pour une logique modifiée, Annexes - voir 6 annexes de logique, ici la Table des matières, Lecture des formules kantique de la sexuation 2009 et 2012 résumé, JMV, IV-SEPARATION (articulation des Théories axiomatiques et modification de la logique L3T3 dans le graphe ) - voir Post, - Panorama, .html, |
||||||||||||||||||||||||||||||||||||||||||||
✔ |
- Avant de trouver son nom actuel, attribué à Giuseppe Peano, la logique mathématique s'est appelée « logique symbolique » (en opposition à la logique philosophique), « métamathématique » (terminologie de Hilbert) et « idéographie » (Begriffsschrift) (terminologie de Frege). in wikipedia, Logique mathématique, | |||||||||||||||||||||||||||||||||||||||||||||
Lois de composition↑ |
✔ |
-Les structures algébriques sont toujours définies pour un type d'objet précis : un domaine ou une loi de composition. Ensuite elles le sont par des axiomes. Donc les axiomes varient avec les structures. Leurs propriétés sont attachées à des modes de compostion d'éléments. Il faut définir le domaine où s'effectuent les combinaisons et les moyens d'obtenir le résultat de la compositions, ce sont les lois des mathématiciens. Essaim p 36. La loi de composition et son domaine d'effectuation propre s'appelait auparavant une opération (la somme, le produit, dans le domaine numérique, mais la soustraction et le quotient vont se trouver traités différemment). |
||||||||||||||||||||||||||||||||||||||||||||
Lois freudiennes ↑ |
✔ |
au même titre que nous observons -les Lois de la science, les lois des corps, de la gravitation, de l'attraction, les lois de Newton ainsi que -les lois humaines, conventionnelles, celles des sujets, encadrées par les parlements, les traditions, la Justice, la police, ces lois que les Hommes s'efforcent de transgresser, de déjouer, qui mettent en relation la violence individuelle face à la violence publique il existe -les lois freudiennes, contraignantes, que l'on peut aussi déjouer mais qui alors se déforment, se transforment, s'inversent. Suivre les impératifs du Surmoi ne fait que le renforcer. Ne pas tenir compte du Surmoi, crée la clinique de la délinquance, ou l'hypermoralité. On peut mésuser de la sexualité non sans culpabilité ! On peut tricher avec ses lois au prix des symptômes |
||||||||||||||||||||||||||||||||||||||||||||
lois de la parole ↑ |
✔ |
= fonction imaginaire du phallus symbolique : opérateur évanescent effectif réel voir aussi ici, + compléments sur le graphe de la lettre 52, les schémas RFL & les noeuds, & les Discours |
||||||||||||||||||||||||||||||||||||||||||||
Logique linéaire J-Y GIRARD |
✔ |
En logique mathématique et plus précisément en théorie de la démonstration, la logique linéaire, inventée par le logicien Jean-Yves Girard en 1986, est un système formel qui, du point de vue logique, décompose et analyse les logiques classique et intuitionniste et, du point de vue calculatoire, est un système de type pour le lambda-calcul permettant de spécifier certains usages des ressources. La logique classique n'étudie pas les aspects les plus élémentaires du raisonnement. Sa structure peut être décomposée dans des systèmes formels plus élémentaires qui décrivent des étapes plus fines de la déduction ; en particulier, il est possible de s'intéresser à des logiques où certaines règles de la logique classique n'existent pas. De telles logiques sont appelées des logiques sous-structurelles. L'une de ces logiques sous-structurelles est la logique linéaire ; il lui manque en particulier la règle de contraction de la logique classique qui dit en gros que si on peut faire un raisonnement avec une même hypothèse invoquée deux fois, on peut faire le même raisonnement sans dupliquer cette hypothèse et la règle d'affaiblissement qui permet d'éliminer de l'ensemble des hypothèses une hypothèse inutilisée dans le raisonnement. - voir Jean-Yves GIRARD, |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Logique modale | ✔ |
- Logique modale : En logique mathématique, une logique modale est un type de logique formelle qui étend la logique propositionnelle, la logique du premier ordre ou la logique d'ordre supérieur avec des modalités. Une modalité spécifie des qualités du vrai. Par exemple, une proposition comme « il pleut » peut être précédée d'une modalité :
Il existe une variété de logiques modales comme les logiques temporelles, la logique épistémique (logique de connaissance). En informatique, la logique modale est utilisée pour son expressivité et les aspects algorithmiques. Par exemple, la logique temporelle est utilisée pour spécifier des programmes puis les vérifier. ...source W, |
||||||||||||||||||||||||||||||||||||||||||||
| Logique du premier ordre | ✔ |
- La logique du premier ordre introduit des symboles nommés variables, des symboles nommés prédicats (relations), des connecteurs logiques (∧, ET; ∨, OU) , et deux quantificateurs logiques : l'un universel ∀( pour tout) et l'autre existentiel ∃(il existe) . Premier ordre par rapport aux logiques d'ordre supérieures. |
||||||||||||||||||||||||||||||||||||||||||||
Logique du second ordre |
✔ |
- elle étend la logique du premier ordre par ajout de variables relationnelles qui peuvent être quantifiées | W, |
|||||||||||||||||||||||||||||||||||||||||||
| LT ST |
✔ | Langage, (Langue); Théorie, Système d'écriture, Syntaxe; Théorie, |
Math et schema L, L1, L2, F, .swf, |
|||||||||||||||||||||||||||||||||||||||||||
| Mathématiques, | ✔ | Topologie générale, TG, Théorie des catégories, Cs, m...i, Secondaire, Symboles; , La topologie générale est une branche de la topologie qui étudie les propriétés des espaces topologiques et des structures définies sur ces ensembles. Contrairement aux autres notions de topologie, elle se distingue par son caractère plus universel, notamment pour les espaces topologiques. W, La théorie des catégories étudie les structures mathématiques et leurs relations. L'étude des catégories, très abstraite, fut motivée par l'abondance de caractéristiques communes à diverses classes liées à des structures mathématiques. Les catégories sont utilisées dans la plupart des branches mathématiques et dans certains secteurs de l'informatique théorique et en mathématiques de la physique. Elles forment une notion unificatrice. W, |
||||||||||||||||||||||||||||||||||||||||||||
| Les catégories Langage, Syntaxe ou Systèmes d'écriture, Théorie sont indiciées, elles ne le sont souvent pas par ....paresse ! | ||||||||||||||||||||||||||||||||||||||||||||||
| L0T0( L0T0) S0T0 (S0T0) |
Théorie des ensembles, Pcs, |
F, | ||||||||||||||||||||||||||||||||||||||||||||
| L1T1 S1T1 |
✔ |
Calcul des prédicats, Quantification, Ics, La logique du premier ordre introduit des symboles nommés variables, des symboles nommés prédicats (relations), des connecteurs logiques (∧, ET; ∨, OU) , et deux quantificateurs logiques : l'un universel ∀( pour tout) et l'autre existentiel ∃(il existe) . Quantification/kantification, |
Math et schema L, L1, L2, F, .swf, |
|||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
| L2T2 S2T2 |
✔ | Calcul des propositions, calcul des énoncés, calcul de la coordination, Premier, signes et langue parlée, Négation classique : ¬, implication : ⇒ des connecteurs logiques (∧, ET; ∨, OU), Premier, Ps (Perceptions signes), parole animale et langue parlée, signes, parole, Vérification et vérifonctionnalité, V-F, 1,0; Algèbre de Boole, Logique modale, ◊ , ∅ La LCC ( I ....Ics, S1T1, S2T2) produit la Théorie des ensembles, (S0T0) LCC (Logique canonique classique est l'agencement de la théorie de la vérifonctionnalité (L2T2) et de la théorie de la kantification, (L1T1)) |
F, | |||||||||||||||||||||||||||||||||||||||||||
| L3T3 S3T3 |
✔ | Topologie du sujet, Logique modifiée, Négation modifiée, Premier, |
F, | ↑ | ||||||||||||||||||||||||||||||||||||||||||
| La Logique modifiée est une logique construite d'une manière linéaire sur une Algèbre de Boole.voir JMV juin 2015, Algèbre de Boole , est de caractéristique 2 (0,1); qui a pour éléments 2 puissance n, pour 2 : (00, 01, 10, 11); pour 3 : (000, 001, 010, 011, 100, 101, 110, 111); C'est une extention des dimensions de la LCC. |
Math et schema L, L1, L2, F, .swf, |
|||||||||||||||||||||||||||||||||||||||||||||
Le plongement de la logique classique dans la logique modifiée permet de former, d'écrire, côté femme, |
||||||||||||||||||||||||||||||||||||||||||||||
Effectivité |
✔ | Entre Cs et P, (Conscience et Perception) , ente m.i et M.I, | ↑ | |||||||||||||||||||||||||||||||||||||||||||
| - c'est l'enchainement (JMV020914-39.42) - un discours qui se tient, qui est enchainé, c’est là que la notion de chaine va apparaître en tant qu’elle représente l’effectivité, de quelque chose d’effectif, qui tient, quand on tire dessus dans tous les sens, ça tient, et c’est ça qui fait, c’est ce que moi j’appelle effectivité, et que j’oppose à la réalité qu’on voudrait nous imposer, surtout de plus en plus, du fait, c’est pas seulement du fait de l’influence du Cercle de Vienne, et du logico positivisme, même avant Russel, il faisait déjà du logico-positivisme, Bertrand Russell, donc la question de l’effectivité, en allemand, au début des Ecrits, vous verrez ça, Lacan en parle dans ses antécédents, il souligne cette différence chez Freud entre Realitad et Virtsgeigt et le virlitsgeit, c’est deux manière de parler de la réalité, et Virtgeigt, il y en a une qui s’appelle effectivité, je propose de le traduire par effectivité, si on fait quelque chose effectivement, peut être y-a-t-il du mensonge, mais pourquoi le mensonge ne serait pas lui-même effectif, le mensonge c’est bien lié au fait de dire, et ça a une effectivité le fait de dire, c’est même la fonction phallique, par excellence, JMV23062015 |
||||||||||||||||||||||||||||||||||||||||||||||
| Lukasiewicz | ✔ |
- la logique de Lukasiewicz même si Lukasiewicz était très timide, très timoré, c’est un grand logicien, V01-43.52 ; son analyse et sa lecture de la syllogistique d’Aristote, qu’il a mené pendant 50 ans, c’est quelque chose de magnifique, c’était presque prêt à publier en 19o5, il l’a publié en 1955, et dans le cours du bouquin, il vous raconte qu’à un endroit il s’est trompé et il a modifié son point de vue, et son écriture, au moment où il découvre ça, c’est René Guitart qui s’en est aperçu, en lisant tout le bouquin, mais en plus Lukasiewicz il lit Aristote en Grec, il fait des notes, il commente tout le texte de la Syllogistique et de l’Organon en grec, c’est un truc formidable, JMV20150602 | ||||||||||||||||||||||||||||||||||||||||||||
| M | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
| Machine (Mécanique) |
✔ |
- comment parler à partir de là du Trieb ?, vous voyez que quand le symbolique tombe dans le corps, sur le corps, traverse le corps, il y a une très belle phrase de Lacan dans La direction de la cure où il dit que c’est jamais simple, que le névrosé est pas mal placé dans l’être, parce qu’il se plaint de ce passage, le névrosé se plaint parce que pour lui c’est une peine, donc il n’est pas question de dire qu’il faut se satisfaire de cette peine, mais le fait est que c’est effectivement une peine pour le sujet de se trouver être l’agent qui fait entrer le symbolique dans le monde et c’est ensuite par ses actions et y compris par l’écriture qu’il va modifier le monde, qu’il va transformer le monde, nous sommes des sujets ségrégatifs parce que le signifiant a cette structure qui est celle déjà avec la parole et ensuite avec l’écriture, le signifiant et la lettre ont toujours cette dimension de quelque chose qui se dédouble, 51.40, ça s’appelle la répétition freudienne, c’est ce que Freud va rencontrer dans les années 1920, c’est ce que Lacan appelle dans les Séminaires des années 1960, la grande différence, c’est cette pulsation qu’il y a à l’intérieur du symbolique, qui fait que c’est quelque chose qui n’a rien à voir avec la Nature, et même si ça va nous permettre d’inventer les machines , nous sommes la seule espèce animale qui inventons des machines, et même des machines électroniques, on a commencé par des machines à vapeur, on a même commencé par des outils, mais n’empêche que ça va nous permettre de construire des nouvelles machines, et c’est le fonctionnement de ce dédoublement et de cette identité, de cette pulsation qui fonctionne aussi dans nos machines mais qui fonctionne d’une manière spéciale dans le symbolique, c’est là qu’il faut distinguer le symbolique de l’ordre mécanique ou électronique, dans la mesure ou vous voyez bien que la machine peut reproduire des choses que vous lui apprenez à faire, mais elle ne va pas inventer ce que vous vous pouvez inventer si vous vous racontez des histoires, ou bien aussi des mathématiques, par exemple la découverte d’une démonstration en mathématique ne se fait pas d’une manière automatique, 52.58, .... ... - Le CUNN.Yann (W) : les fameux neurones artificiels. Ceux-ci n’ont rien de matériel. Ce sont en fait des fonctions mathématiques à plusieurs paramètres ajustables. Dans les neurones du cerveau, des connexions se créent, disparaissent ou se renforcent, en fonction de différents stimuli. Dans le monde artificiel, on ajuste des paramètres afin de fournir la meilleure réponse possible. « On représente le monde en une suite de nombres, qui sont autant de vecteurs de la pensée » La machine qui comprendra un texte n’existe pas encore? Disons que c’est un peu un rêve, même si le but semble aujourd’hui relativement atteignable. Quelquefois les questions que l’on pose ne sont pas très compliquées (les heures d’ouverture d’un restaurant, par exemple), mais si l’information n’est pas structurée, ce ne sera pas facile de la trouver. Et une machine ne saura pas répondre à une question plus complexe, par exemple : « Antoine prend le planeur, le lance du balcon, puis va le chercher. Où est parti Antoine ? ». Répondre à cette question requiert du sens commun: le fait que le planeur est un jouet, qu’il finira par atterrir dans la rue ou le jardin, que pour aller le chercher Antoine devra descendre des étages, etc. Nous devinons tout cela grâce à notre expérience du monde qui nous entoure. in les Echos, B.GEORGE 15 juin 2015 - Machine et organisme, CANGUILHEM, W , Oeuvre, - HEPHAÏSTOS : gaogoa, |
|
|
||||||||||||||||||||||||||||||||||||||||||
| Machine et noeuds | - JMV in La Topologie et le temps,Lacan, Séminaire 23- TT15051979, Machines mathématiques, |
|||||||||||||||||||||||||||||||||||||||||||||
Management↑ |
✔ |
- dans le management, le préfixe mana est éloquent, (efficacité et magie), c'est un retour au discours du Maitre, mode animal, éthologie, et si la compétition, l'agressivité et la ruse en sont les piliers, il y a une attirance pour les techniques de stress du corps, pour les effets de groupe, l'hystérie, la perversion et la recherche d'un certain frisson...!, (canyoning, marcher sur des braises, acrobranche, humiliations, ...), tout ceci est constitutif de l'initiation rituelle des sociétés traditionnelles avec en arrière plan une note sexuelle à peine voilée... C'est le culte du père de la préhistoire et de ses attributs. ( Le père et le phallus enterrés dans le même sac !). La pyramide ne pointe pas vers le soleil, mais vers la pointeuse, l'exploitation et le Kapital. Le sujet y est forclos sauf assujetti et muet. Le management conditionne autrui à ses fins, et aux fins des actionnaires : la rentabilité. Les mathématiques y sont aliénées et rabaissées à la numérisation et à la comptabilité. Principal vecteur de folie occidenté !. | ||||||||||||||||||||||||||||||||||||||||||||
Massacre(s) |
✔ |
- nous avons fait une grande découverte : il faut savoir lire pour inventer une écriture, moi je tiens que c’est quelque chose d’absolument innovant, je ne comprends pas que la psychanalyse de Freud et fondée par Lacan, qui est le discours le plus innovant que l’on connaisse dans l’occident christianisé, ce discours est disqualifié par tous les adeptes qui réduisent ça en peau de chagrin ou en serpillère, regardez ce que ça donne aujourd’hui, ça recommence, voyez, on ne sait toujours pas entendre ce que font les paranoïaques quand ils veulent massacrer, détruire, le Symbolique dans le corps de leurs victimes, vous avez Auschwitz, Hiroshima, ça ne sert à rien, ils sont même allés jusqu’à massacrer les gens, en les mettant « en ligne », sur Internet, pour terroriser tout le monde, et en même temps ils détruisent les Musées, et les sites archéologiques, c’est de la paranoïa, le crime paranoïaque des Sœurs Papins, qui fascinait Musil, qui fascinait Jean Genêt, et sur laquelle Lacan a écrit, nous avons la réponse grâce à la psychanalyse, nous savons qu’est ce que c’est que ce crime, des sérials killers, pédophiles ou non, que leurs victimes soient adultes femmes, enfants, tout ce qu’on veut, tout le monde est là en train de leurs demander, l’Avocat, le Juge, la partie civile dans les tribunaux, on leurs demande : mais pourquoi ? pourquoi tant de violence ?, et ils ne peuvent pas répondre ! Bien sûr qu’ils ne peuvent pas répondre, parce que pour répondre il faut lire Freud, Lacan, faire une analyse, et d’ailleurs c’est la seule manière d’arrêter ce massacre. L’autre manière étant de les tuer tous ! C’est ce qui s’est passé avec les nazis, on les a gagnés militairement, mais je ne crois pas que le procès de Nuremberg ait apporté le moindre éclairage à la question : Pourquoi Auschwitz ? Pourquoi cette violence, et cette organisation hyper industrielle, du meurtre paranoïaque de masse, et ça recommence, et moi je dis que c’est un crime politique, puisque c’est favorisé par les discours démagogiques de ceux qui disent que le Langage ne sert à rien, que le Symbolique ne sert à rien, qu’on veut faire un monde uniquement avec La Nature et Les Machines, je vous invite à aller dans les couloirs de Roissy et Orly, vous vous baladez dans les passages qui vous conduisent à l’avion, vous avez les publicités HSBC, y a un panneau qui dit ça, il vous dessine une guêpe et puis il y a un ordinateur portable, et ils vous disent : la Nature et l’Informatique collaborent pour l’avenir de demain ! |
||||||||||||||||||||||||||||||||||||||||||||
Matemata↑ |
✔ |
- ce qui s'enseigne par excellence, ce qui peut être appris... - Psychanalyse et mathématique, Freud contemporain de Cantor, JMV, 2007 |
||||||||||||||||||||||||||||||||||||||||||||
| Mathématiques, | ✔ |
Les mathématiques (ou la mathématique) sont un ensemble de connaissances abstraites résultant de raisonnements logiques appliqués à des objets divers tels que les ensembles mathématiques, les nombres, les formes, les structures, les transformations, etc. ; ainsi qu'aux relations et opérations mathématiques qui existent entre ces objets. Elles sont aussi le domaine de recherche développant ces connaissances, ainsi que la discipline qui les enseigne. Elles possèdent plusieurs branches telles que : l'arithmétique, l'algèbre, l'analyse, la géométrie, la logique mathématique, etc. Il existe également une certaine séparation entre les mathématiques pures et les mathématiques appliquées. Les mathématiques se distinguent des autres sciences par un rapport particulier au réel car l'observation et l'expérience ne s'y portent pas sur des objets physiques ; les mathématiques ne sont pas une science empirique. Elles sont de nature entièrement intellectuelle, fondées sur des axiomes déclarés vrais ou sur des postulats provisoirement admis. Ces axiomes en constituent les fondements et ne dépendent donc d'aucune autre proposition. Un énoncé mathématique – dénommé généralement, après être validé, théorème, proposition, lemme, fait, scholie ou corollaire – est considéré comme valide lorsque le discours formel qui établit sa vérité respecte une certaine structure rationnelle appelée démonstration, ou raisonnement logicodéductif. Un énoncé qui n'a pas encore fait l'objet d'une démonstration mais qui est néanmoins considéré plausible est appelé conjecture. Bien que les résultats mathématiques soient des vérités purement formelles, ils trouvent des applications dans les autres sciences et dans différents domaines de la technique. C'est ainsi qu'Eugene Wigner parle de « la déraisonnable efficacité des mathématiques dans les sciences de la nature ». |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Mathématique(s) |
- Domaines ( classiques) des mathématiques : VILLEMIN.G, - Vappereau Jean-Michel : les mathématiques, c’est une manière d’écrire dans le Privé, en s’imposant la Loi de la parole, pour ce qu’on écrit, - voir Entête de cette page, diverses définitions... - Les Eléments de mathématique de N.Bourbaki prennent le concept de structure comme concept fondamental : ils présentent les mathématiques comme le science des structures. Ainsi la théorie des ensembles ordonnés étudie en fait les structures d'ordre, c'est-à-dire les structures définies par une relation d'ordre. - Une partie des mathématiques élémentaires consite à montrer les liens cachés entre l'algèbre et la géométrie. - Lacan et les mathématiques, René.GUITART, 2011, |
|||||||||||||||||||||||||||||||||||||||||||||
| Mathématiques dialectiques | - Parcours mathématique de Lacan, par JMV, | |||||||||||||||||||||||||||||||||||||||||||||
| - La chose freudienne ou Sens du retour à Freud en psychanalyse, p429, Ecrits, p401-436, Seuil, 4 eme page de fin de texte. (ELP, p16, 4 lignes après L'action analytique, dernier quart du texte, voir ci-desssous, Note : Les textes sont inversés sur la site ELP, (in Pas-tout Lacan) 1995-11-07 : Notes en allemand préparatoire à la conférence sur la Chose freudienne * est lié au texte La chose freudienne * ou sens du retour à Freud en psychanalyse, et inversement ,). (Staferla, 3eme ligne après L'action analytique, dernier quart du texte) |
||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
Mathématicien↑ |
✔ |
- le mathématicien(ne), est un sujet qui a intériorisé et intégré une loi. Intégré la loi de la parole dans une pratique intime de l'écriture. (Il est de ce fait, assez souvent, mais pas toujours, du côté du manche !) - Mathématiciens et logiciens - Mathématiciens des noeuds - La logique, |
||||||||||||||||||||||||||||||||||||||||||||
| Le terme générique mathématicien peut se décliner pour des domaines plus restreints, comme algébriste, analyste, arithméticien, géomètre, logicien, probabiliste, etc. | ||||||||||||||||||||||||||||||||||||||||||||||
| Les mathématiciens s'imposent une rigueur méthodologique qui peut faire paraître singulière leur discipline. Le formalisme et l'exposition rigoureuse des travaux, y compris des phases intermédiaires, sont des points estimés nécessaires à l'acceptation des résultats obtenus. Le travail de vérification, ou de réfutation le cas échéant, des résultats présentés par d'autres mathématiciens, fait également partie de l'activité d'un mathématicien. Pour certains exposés particulièrement complexes ou difficiles, ces vérifications peuvent nécessiter la contribution de plusieurs mathématiciens travaillant de manière concertée. | W, |
|||||||||||||||||||||||||||||||||||||||||||||
Mathème↑ |
✔ |
- Les lettres, les mathèmes, sont des symboles dont use Lacan à des fins de formalisation et de transmission. Elles sont les éléments d'une algèbre à venir, mais qui n'existe pas, et d'une « mathématisation » qui n'en a que le nom puisqu'elle exclut tout calcul et se réduit à quelques symboles indissociables du long discours qui les explicite. Pour l'essentiel, ils sont au nombre de quatre. Une paire de signifiants, S 1 et S 2 , réduction de la chaîne signifiante à deux éléments, le signifiant unaire et le signifiant binaire. Ils suffisent à écrire et définir le sujet /S. Sujet barré par le signifiant, - les mathèmes de Lacan, J.Siboni - Psychanalyse et mathématique, Freud contemporain de Cantor, JMV, 2007 |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Mémoire | ✔ |
- la mémoire dépend de la syntaxe, et n'est pas sans sujet ! ( JMV23062015) - Voir Mémoire et Rhétorique, in LOGIQUE, ou hors cadre : Mémoire et Rhétorique, gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
Métalangage ↑ |
✔ |
- c’est Tarski qui a introduit la notion de métalangage en logique, il s’est rendu compte en réfléchissant sur cette condition d’emploi du prédicat de vérité, que pour qu’il n’y ait pas de contradiction dans une théorie, il faut que le prédicat de vérité soit écrit dans le commentaire mais ne fasse pas partie du langage objet, 36.27, c’est de là que vient la notion de métalangage, des travaux de Tarski. (JMV27012015) - Il y a et il n'y a pas de métalangage. (Je parle toujours dans la langue, même du métalangage !) - L'amour du tout aujourd'hui, 1ere partie , la fonction phallique, Cs et Ics avec Wundt, Tarski, prédicat de V, induction déduction, assimilation, métalangage, - La LCC, in L'amour du tout aujourd'hui, 2 eme partie, JMV, 1992 - l'amour du tout, partie 3, 1992, JMV |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Métaphore ↑
|
✔ |
- La métaphore traduit le triangle S (PIM) du Schéma R, (LACAN, Ecrits, p 553, D'une question préliminaire à tout traitement possible de la psychose, Seuil,) où s'articule la manière dont le signifiant du père vient assumer la fonction de puissance et de tempérament, qui arbitre la tension jalouse, au fondement de cet espace (La Mère, son désir représenté par le phallus et le rival fraternel, et l'enfant siuté en I, côté idéal. C'est aussi la structure de la pudeur, c'est la fonction imaginaire du phallus symbolique.
- Formule de la .... Les noms du père, Ecole Lacanienne de Tokyo : par Luke Shinya Ogasawara |
||||||||||||||||||||||||||||||||||||||||||||
Milnor↑
|
✔ |
- Milnor, wiki, - Chaine presque triviale de Milnor, noeud borroméen, voir Borroméen, ou noeud borroméen, - Links Group, 1952, - Isotopy of links, 1957, - Somme de variétés différentiables..., 1959, |
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
Miroir↑
|
✔ |
- Miroir plan : une surface plane réfléchissante constitue un miroir plan - voir Stade du miroir - Deux aspects géométriques du narcissisme, JMV 17 mai 2011 - Vel de l'aliénation,<≠ JMV 2006, |
||||||||||||||||||||||||||||||||||||||||||||
Modal ↑ |
✔ |
-
Réponse possible ou attribut d'une donnée d'une distribution d'un caractère statistique qualitatif . - En logique mathématique, une logique modale est un type de logique formelle qui étend la logique propositionnelle, la logique du premier ordre ou la logique d'ordre supérieur avec des modalités. Une modalité spécifie des qualités du vrai. Par exemple, une proposition comme « il pleut » peut être précédée d'une modalité :
Il existe une variété de logiques modales comme les logiques temporelles (ajout d'une modalité conditionnelle - selon l'évolution- transformateur de prédicat liée au temps), la logique épistémique (logique de connaissance). En informatique, la logique modale est utilisée pour son expressivité et les aspects algorithmiques. Par exemple, la logique temporelle est utilisée pour spécifier des programmes puis les vérifier. |
W, | |||||||||||||||||||||||||||||||||||||||||||
| Modalité | ✔ | Une modalité, dans une logique, est une classe dans laquelle on peut classer les propositions logique comme "possible", nécessaires, toujours valides... Les logiques modales sont des exemples de logiques définies selon des ensembles différents de modalités de l'ensemble de modalité de la logique classique, en étendant cette dernière. | W, | |||||||||||||||||||||||||||||||||||||||||||
| - voir gaogoa, LOGIQUE, Rhétorique, Aristote, La logique modale, | ||||||||||||||||||||||||||||||||||||||||||||||
Moebius |
✔ |
- Moebius, - Moebius, la bande de, - Moebius dans le tore, JMV16062015, L240 - moebius et plan pojectif, cercle, - Moebius et cross-cap, |
||||||||||||||||||||||||||||||||||||||||||||
Mécanique quantique
Physique, ... |
✔ | - La mécanique quantique est la branche de la physique théorique qui a succédé à la théorie des quanta et à la mécanique ondulatoire pour étudier et décrire les phénomènes fondamentaux à l'œuvre dans les systèmes physiques, plus particulièrement à l'échelle atomique et subatomique.
Elle fut développée dans les années 1920 par une dizaine de physiciens européens, pour résoudre des problèmes que la physique classique échouait à expliquer, comme le rayonnement du corps noir, l'effet photo-électrique, ou l'existence des raies spectrales. Elle se montra féconde en résultats et en applications diverses : elle permit notamment d'élucider le mystère de la structure de l'atome, et plus globalement elle s'avéra être le cadre général de description du comportement des particules élémentaires, jusqu'à constituer le socle de la physique moderne. La mécanique quantique comporte de profondes difficultés conceptuelles. Si son formalisme mathématique est d'une efficacité inégalée note 1, son interprétation ne fait pas l'unanimité dans la communauté scientifique1. Parmi ses concepts, on peut citer la dualité onde corpuscule, la superposition quantique, l'intrication quantique ou encore la non-localité. L'expression physique quantique désigne le corpus théorique plus étendu qui s'appuie sur la mécanique quantique pour décrire un ensemble plus vaste de phénomènes, dont les interactions fondamentales dans le modèle standard. Un quantomécanicien est un spécialiste de mécanique quantique et un quantochimiste un spécialiste de chimie quantique |
↑ | |||||||||||||||||||||||||||||||||||||||||||
| Monstre Monstruosité |
✔ |
- Canguilhem... arrive à spécifier l’organisme, il le spécifie par un trait distinctif qui s’appelle : la persévérance, l’organisme persévère parce qu’il tente de se réparer malgré tous les défauts, tous les déboires, donc là vous avez quelque chose qui fait penser qu’on se rapproche du Symbolique avec l’organisme, et bien c’est une erreur de confondre cette persévérance organique, alors vous voyez bien que le thème de la sexualité va être convoqué là, entre organisme et symbolique, c’est justement là qu’il faut situer précisément la différence entre sexualité c’est-à-dire reproduction, et sexe, c’est-à-dire différence d’un type qui est exceptionnelle, qui est du Symbolique, cette grande différence, cette répétition freudienne, donc vous avez là quelque chose que Canguilhem ne va pas achever dans cet article, ( Machine et organisme), il n’arrive pas à le dire, c’est ça qui est magnifique, c’est que son enquête le conduit à trouver le trait distinctif de la persévérance mais il n’arrive pas à conclure, et il l’écrit après ça, d’ailleurs chez Vrin ils ont mis l’article tout de suite après, un autre article qui nous donne la clé, un autre article qui s’appelle : Le monstrueux et la monstruosité, qu’est ce que ça veut dire, ça veut dire comme le dit Canguilhem que les organismes fabriquent des monstres, puisqu’il persévère, les moutons à cinq pattes, les siamois, c’est ce qu’on considère, on en a même montrés dans des cirques, ça fascine les sujets du Symbolique, Le monstre, et il fait remarquer qu’il n’y a pas de monstre géologique, on ne dit pas qu’une montagne ou un rocher et monstrueuse, on dit qu’elle est énorme, qu’elle est massive, mais on ne dit pas qu’elle est monstrueuse, l’idée très fabriquée de considérer qu’il y a des monstres, que même les animaux préhistoriques sont des monstres, ce sont pas des monstres ce sont des Animaux, le monstrueux vous allez voir ça, vous allez à la Grande Galerie, vous allez voir des flacons avec des moutons à cinq pattes, des frères siamois dans du formol, YX- je les ai vu , au sous sol ! JMV : oui, au sous-sol, ils ont toujours été là depuis des années, c’est toujours fascinant, on a toujours montré ça dans les cirques, vous avez Eléphantman, un film qui est justement de l’ordre de ce phantasme, c’est un monstre, c’est un homme, c’est un animal, qu’est-ce-que c’est ? Vous avez là quelque chose qui est décisif, parce que l’insuffisance organique du monstre que nous sommes, nous nous sommes des monstres, Monstruosité, autisme, psychose, narcissisme, incorporation, nous sommes des prématurés inviables, et c’est ne nous accrochant à la déformation par le Trieb, parce qu’on n’appelle pas bien : Pulsion, par la déformation du Symbolique que nous allons réussir à surmonter cette prématuration organique,... JMV16062015, - La connaissance de la vie, Machine et organisme, p101, p118, Le normal et le pathologique, p155, La monstruosité et le monstrueux, p171, Canguilhem, |
||||||||||||||||||||||||||||||||||||||||||||
Monadique↑
|
Monadique, adj. a) Philos. [Correspond à supra A 2 b] Qui se rapporte à l'individualité en tant qu'unité, totalité close ou qui en a la nature. La thèse muette de la perception, c'est que l'expérience à chaque instant peut être coordonnée avec celle de l'instant précédent et avec celle de l'instant suivant, ma perspective avec celle des autres consciences, (...) que toutes les contradictions peuvent être levées, que l'expérience monadique et intersubjective est un seul texte sans lacune (Merleau-Ponty, Phénoménol. perception, 1945, p.66). Aucune existence dans la perspective biblique n'est monadique, toute existence est relation avec un autre ( Philos., Relig., 1957, p.40-1). b) Qui concerne une personne ou une chose en tant qu'être unique. L'antithèse [ unité de nature, triplicité de personnes ] ne semble guère facile à admettre, mais elle a ceci de bon qu'elle exclut toute possibilité d'enclore le mystère de Dieu, soit dans une structure monadique, soit dans une structure triadique ( Philos., Relig., 1957p.38-13). − [mɔnadik]. − 1 re attest. 1931 ( Méditations cartésiennes, trad. du texte all. de E. Husserl, Introd. à la phénoménol. par G. Peiffer et E. Levinas, Paris, A. Colin, p.87); de monade, suff. -ique *; cf. angl. monadic att. au sens gén. en 1788 et en réf. à Leibniz en 1862 ds NED. (sur TLFI) - voir Leibniz, la Monadologie, |
|||||||||||||||||||||||||||||||||||||||||||||
Monades : Une monade est une force irréductible, qui contient en elle-même le principe et la source de toutes ses actions. Les monades sont les éléments de toutes les choses, tant matérielles qu'incorporelles. Elles ne se forment ni ne se décomposent; elles ne peuvent subir aucune altération, aucune modification par un changement interne; elles ne naissent ni ne périssent; toutes datent du jour de la création. Le monde est à leur égard dépourvu d'action, et, suivant les expressions de Leibniz, en elles n'existent ni portes ni fenêtres qui puissent leur donner accès. Elles n'ont ni étendue ni figure, et ne peuvent occuper d'espace ou se trouver dans un lieu. |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
... elles sont privées de mouvement. Cependant, malgré leur simplicité absolue, aucune monade n'est semblable à une autre. Elles diffèrent entre elles par certaines propriétés ou qualités qui leur sont inhérentes. Leibniz attribue à toutes ses monades des perceptions, et, avec la perception, il place dans chacune d'elles une tendance à passer d'une perception à une autre, qui est le principe de son changement et qu'il nomme appétition. Dans chaque monade l'appétition répond à la perception, comme en nous la volonté répond à l'intelligence. C'est par ces actions internes que les monades, suivant Leibniz, diffèrent entre elles. En outre, de la diversité de ces perceptions et appétitions il résulte non seulement une variété infinie, mais encore une hiérarchie entre toutes les monades. Depuis la plus intime, qu'on peut se représenter comme une simple force de cohésion, on monte, par une suite non interrompue de degrés presque insensibles, jusqu'à celles dans lesquelles la perception est plus distincte et révélée par la conscience; ce sont les âmes proprement dites. Les âmes humaines se distinguent de celles des animaux par la connaissance des vérités-nécessaires, qui constituent la raison. Mais s'il y a suite et enchaînement entre les monades, il n'y a point entre elles de réciprocité d'action et d'influence. Toutes les actions internes d'une monades dépendent invariablement de la seule force qui est en elle; Dieu lui-même, dès l'origine des choses, a mesuré cette force et en a réglé toutes les perceptions. En construisant sa Monadologie, ou sa théorie des monades, Leibniz avait pour objet de combler l'abîme qui existe entre la matière et l'esprit, et de faire concevoir leur union. |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
Le monadisme, vitaliste, s'oppose à l'atomisme, qui est mécaniste. La science des monades s'appelle « monadologie » ; ce néologisme vient, non de Leibniz, mais de Erdmann, l'éditeur de Leibniz en 1840. Quant aux mots, on peut dire que, parfois, le Grec appelle les nombres arithmétiques un, deux, trois, quatre, cinq, dix..., tandis qu'il appelle les nombres idéaux monade, dyade, triade, tétrade. D'autre part, par convention, le mot « Monade » (avec majuscule) désigne le principe un, l'Un, l'Unité, tandis que « monade », avec minuscule, désigne une unité, une substance simple. Quant aux concepts, on peut distinguer ou confondre Un et Monade. Les pythagoriciens semblent les identifier, les platoniciens les distinguer : dans son enseignement oral, Platon pose deux principes contraires, au sommet l'Un, en bas la Dyade, ce ne sont pas des nombres, mais les sources des nombres : « C'est à partir de cet Un que le nombre idéal est engendré », « la Dyade indéfinie est génératrice de la quantité », et l'Un engendre les nombres idéaux de la Décade (monade, dyade, triade, tétrade). |
et sur W, |
|||||||||||||||||||||||||||||||||||||||||||||
| Morgan, De ; Morganien |
||||||||||||||||||||||||||||||||||||||||||||||
Biographie |
Auguste (ou Augustus) De Morgan (27 juin 1806 à Madurai (Tamil Nadu) - 18 mars 1871) est un mathématicien et logicien britannique, né en Inde. Il est le fondateur avec Boole de la logique moderne ; il a notamment formulé les lois de De Morgan. source et suite sur Wikipedia, - Lire aussi,
|
|||||||||||||||||||||||||||||||||||||||||||||
✔ |
- une différence morganienne d'aspect s'anime de ce qu'un choix forcé le rend dissymétrique. Autres écrits, p323 La logique du fantasme, comptre rendu du séminaire, 1966-1967, (Texte disponible sur ELP, Pas-tout Lacan, 1960-1969, noté 1968-07-00,). -Le vel de l'aliénation, 2006, JMV LACAN, Séminaire XIV, 11 janvier 1967, |
|||||||||||||||||||||||||||||||||||||||||||||
| - Le groupe de Klein, : Groupe produit, commutatif mais non cyclique, voir Chronomath, | ||||||||||||||||||||||||||||||||||||||||||||||
- Critique la théorie de la double quantification de Hamilton. Donne une définition restrictive de la la notion d'univers. Il est le père de la Logique des Relations qu'il développe en étudiant la nature de la copule EST. Il développe un symbolisme propre aux relations. |
||||||||||||||||||||||||||||||||||||||||||||||
- Lois de De Morgan : |
Les lois de De Morgan sont des identités entre propositions logiques. En logique classique, la négation de la disjonction de deux propositions est équivalente à la conjonction des négations des deux propositions, ce qui signifie que « non(A ou B) » est identique à « (non A) et (non B) ». Toujours en Logique classique, la négation de la conjonction de deux propositions est équivalente à la disjonction des négations des deux propositions, ce qui signifie que « non(A et B) » est identique à « (non A) ou (non B) ». |
|||||||||||||||||||||||||||||||||||||||||||||
| Formules de De Morgan en lien à la Structure Logique du Sujet divisé, source cours de JMV du mardi 15 juin 2010, 3 planches, | ||||||||||||||||||||||||||||||||||||||||||||||
Mot d'esprit |
✔ |
- le mot d’esprit, et c’est la seule transmission raisonnée, et raisonnable, parce que le sujet malgré même le jugement qu’il va avoir, il va rire, donc il faut une métaphore, c’est par les incorporelles, il faut un mot d’esprit, il faut quelque chose que ce soit savant, érudit ou vulgaire, pour moi le prototype de la lisibilité, c’est le fait qu’un type, on lui raconte une histoire, et il rit, ensuite il va le répéter, c’est la seule transmission profane, et tout ces espèce de curés qui nous parlent du Père, du Nom de baptême, parce qu’il y a les Nom du père, le nom de baptême dans Kripke, c’est le sobriquet, il dit que les logiciens l’appelle Nom de baptême, pourquoi cette référence religieuse, vous voyez bien que le sobriquet c’est un mot d’esprit, vous parlez de quelqu’un dans un groupe, que tout le monde connait, et vous l’appelez Lunette ou Moustache, si le mot est bien trouvé tout le monde pige, tout le monde rigole, et dit que c’est pas mal trouvé, c’est ça le mot d’esprit, et c’est la seule transmission raisonnée, et raisonnable, parce que le sujet malgré même le jugement qu’il va avoir, il va rire, et quand un mot l’a faire rire, il va avoir du mal de s’empêcher d’aller le raconter à quelqu’un ! Mais il y a des sujets qui ne comprennent pas les mots d’esprits ! JMV20150602, .html, |
||||||||||||||||||||||||||||||||||||||||||||
Mouvement Gordien↑ impropre |
✔ |
- Mouvement gordien, impropre, pour les chaines, Noeuds page 143 - noté G - voir Noeud ChapIV , p35,142 , |
||||||||||||||||||||||||||||||||||||||||||||
Mouvement Gordien propre ou Homotopie |
✔ |
- Mouvement gordien propre, ou Homotopie ou mouvement noeud à homotopie régulière, | ||||||||||||||||||||||||||||||||||||||||||||
Mouvement noeud↑
|
✔ |
- mouvement effectué deux fois par Lacan dans le Séminaire le Sinthome, le 10 février 1976, dans le Trèfle, et dans le séminaire Dissolution, le 11 décembre 1979, dans le noeud borroméen, - les noeuds dépendent de ces mouvements noeuds. Les mouvements noeuds il y en a de trois sortes, le mouvement noeud propre, - Plasticité nodale et mouvement noeud, JMV23092014, .pdf, Miroir des formants, .pdf, |
||||||||||||||||||||||||||||||||||||||||||||
Mouvement noeud borroméen |
✔ |
- Mouvement noeud borroméen, c'est la structure borroméenne, JMV23092014, 02.09.43, .pdf, Miroir des Formants, - Noeud, ChapVII, p36,285, -le mouvement nœud, Ni, c’est quand vous avez un Triskel, alterné, et que vous le transformez en triskel alterné de l’autre côté |
||||||||||||||||||||||||||||||||||||||||||||
Mouvement noeud à homotopie régulière ↑ |
✔ |
- Mouvement noeud à homotopie régulière, ou Gordien propre, sur une même fil, défait les croisements - noté H - voir Noeud ChapVII , p 285, |
||||||||||||||||||||||||||||||||||||||||||||
Mouvement noeud hybride ↑ |
✔ |
- Mouvement noeud hybride, sur deux fils - noté Nh - voir Noeud ChapVII , p285 , |
||||||||||||||||||||||||||||||||||||||||||||
Mouvement noeud impropre↑ |
✔ |
- Mouvement noeud impropre , sur trois fils différents - noté Ni - voir Noeud ChapVII , p285 , |
||||||||||||||||||||||||||||||||||||||||||||
Mouvement noeud propre ↑ |
✔ |
- Mouvement noeud propre , sur un même fil - noté Np - voir Noeud ChapVII , p285 , |
||||||||||||||||||||||||||||||||||||||||||||
Mouvement de Reidmaster↑ |
✔ |
- Mouvements de Reidemaster, - grâce à trois générateurs, dits R-mouvements dans le Théorie classique des noeuds, où les noeuds peuvent être déformés sans changer leur identité parles composés des trois mouvements de Reidmaster notés : B1, M2, T3, ( B=boucle, M=maille, T=triskel) - voir Noeud ChapIV , p32,142 , |
||||||||||||||||||||||||||||||||||||||||||||
| Mouvement noeud de Whitehead | ✔ |
- le mouvement de Whitehead ou quart de tour, est un mouvement hybride Nh (sur 2 ronds) - voir également le noeud de Whitehead, même si , néanmoins, le noeud de Whitehead est associé à la structure du Fantasme, donc est pertinent pour l'élaboration du Sujet dans sa cure ! sur le noeud de Whitehead, - pour fantasme voir
|
||||||||||||||||||||||||||||||||||||||||||||
| Mur, Murs |
- du Langage : - dans l'incorporation du langage, car lié au(x) traumatismes, et si vous étiez non conscient alors, l'Autre vous rappelera à l'Ordre du Signifiant, à moins que ce ne soit l'autre, toujours aux petits soins .... - dans la "conceptualistation " (notions, idées, concepts) de situations, par vous inconnues, pour aborder des champs étrangers à votre vocabulaire usuel, de confort, celui où "vous respirez", car le langage est comme un poumon .... (changez de cadre référentiel, linguistique, pour en éprouvez le phénomène...! Il y a une découpe, et une rupture de semblant, destabilisante ..;), ne trouvez pas le mot ...hésitez, ...panique ....... - Rapporter un ensemble, à un groupe de signifiants générateurs... = traversée du Langage .... décompsition atomique du langage, de la langue, de lalangue, |
voir Bords... |
||||||||||||||||||||||||||||||||||||||||||||
| - La languene, 2,(le mur des fo rmants), en langue noeuds , le phare des lacans, mais p-ê..fard !? (en suédois far est le père !) | ||||||||||||||||||||||||||||||||||||||||||||||
| - de la Souffrance : - dans la perte d'objet (amoureux, de vie, d'idéal,..d'autonomie, degré de liberté, ..) - dans les limites (nerveuses?) de votre corps, de vos postures, de vos recherches de l'excès ... (alimentaire, physiques..., sexuels .. performants ...) - Dans ses Limites, la douleur rejoint le plaisir, les extrêmes s'y rencontrent... - la lettre en souffrance ....La lettre volée (p40), et lire Le Séminaire XXVIII, DDQNSPDS, Staferla, autour de la page 65/110, Discours, ..jouissance et souffrance ... : l’étoffe de toutes les jouissances confine à la souffrance, c’est même à ça que nous reconnaissons l’habit; |
||||||||||||||||||||||||||||||||||||||||||||||
| N | ||||||||||||||||||||||||||||||||||||||||||||||
| Narcissisme | ✔ |
- Narcissisme ...suite... - Le corps symbolique de s'incorporer au corps propre fait le corps. Par le recours aux Signifiants le mammifère humain tente de surmonter sa débilité constitutive. Mais l'incorporation des structures du langage n'est pas harmonique, et se construisent sur des restes incorporels insistants, c'est le narcisssisme fait des imperfections irréductibles des coutures de cette constitution de la personne. d'après Etoffe p 28 - Fonction désignée par Freud en 1914 et reprise par Lacan dans le Stade du Miroir (notion de position intrinsèque à son corps et/ou extrinsèque dans la vision de son corps, pour le sujet. Seul univerel pour Lacan .). - noeud imaginaire essentiel ou gît le rapport de l'image à la tendance suicide (instinct de mort ou masochisme primordial de Freud). La mort de l'Homme se reflétant dans les traumatismes de la naissance et du sevrage .. Écrits p 186 |
||||||||||||||||||||||||||||||||||||||||||||
nausée
|
✔ |
la nausée, c'est de désinvestir l'objet de toute sa qualité érotique, quand l'objet n'a plus aucune couleur érotique ça devient quelque chose d'absolument dégueulasse . | ||||||||||||||||||||||||||||||||||||||||||||
Négation
Dénégation ↑ |
✔ |
- la négation logique dans Boole, - la négation ensembliste, JMV16062015 : si vous croyez par exemple que la négation c’est le complémentaire ensembliste, en Logique la négation n’est pas le complémentaire ensembliste, à la rigueur ce serait la négation d’une proposition ou d’un concept, si c’était un ensemble, qu’est ce que c’est que la négation ?, c’est le plus petit ensemble de la famille des sous-ensembles, qu’il faut ajouter à un ensemble pour obtenir l’ensemble complet, je vous montre ça sur un dessin, voir JMV16062015 - l'amour du tout, partie 3, 1992, JMV - Parole et inconscient ,partie III, in Eros et psyche, JMV - Une deuxième négation nouvelle : pas toute, notée : ~, dans L2T2, et troisième négation modifiée Pmacron = (¬p ∧ ¬ ~ p) in lecture des formules kantiques de la sexuation (texte intégral), 2009, JMV, - La dénégation, Freud, |
||||||||||||||||||||||||||||||||||||||||||||
Névrose↑ |
✔ |
- maladie du Surmoi qui consiste pour le sujet à se faire du tort. La névrose est une folie avec laquelle le sujet a décidé de rompre en entrant dans la psychanalyse. d'après Noeud p26 - Voir Identifications séxuées, genrées, X, !!, et Structures freudo-lacanienne du symptôme, sur gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
| Noeud↑ | ✔ | - voir Entrelacs, Noeuds, Tresses, Chaines, Echeveau, sur gaogoa, - JMV in La Topologie et le temps, Lacan, Séminaire 23- TT15051979, - Le noeud c'est la rencontre de la parole et de l'écrit, c'est le lieu où ils capitonnent. |
||||||||||||||||||||||||||||||||||||||||||||
| - Le noeud est un accomplissement de coupure. Noeud, p161, J-M.VAPPEREAU, | ||||||||||||||||||||||||||||||||||||||||||||||
| - Alexander en 1923 explique l'importance des tresses dans la théorie des noeuds, on peut les obtenir tous ! Ce qui permet d'énoncer le théorème d'Alexander : Chaque noeud s'obtient de la cloture d'une certaine tresse . (En fait Alexander a démontré que cette assertion est vraie plus généralement pour les entrelacs, dont les noeuds sont un cas particulier.) d'après Noeuds, Alexei.SOSSINSKY, Seuil, p42, |
||||||||||||||||||||||||||||||||||||||||||||||
| - Les noeuds (ou chaines) ne sont perceptibles que d'une position extrinsèque, et relève de ce narcissisme "externe" : je vois mon image dans le miroir, et tout à a fois je suis dans la réalité du territoire. Ou, je suis dans la réalité du paysage ou du contexte et je me situe sur une carte ou dans la théorie d'un discours. Le noeud est un certain parcours .. S'y opposent, la sphère et le tore... qui relèvent de l'intrinsèque. Les noeuds d'un point de vue intrinsèque sont tous identiques ( puisqu'on en a que peu d'indices...) . voir Objets sur gaogoa, - - Treilli, Huit théories dans l'asile, - Le noeud commence avec cette histoire de narcissisme, c’est une tension subjective entre une position du sujet qui est intrinsèque et une position qui est extrinsèque, dans le champ scopique pour le miroir et c’est vrai aussi pour la voix. JMV20150602. (.pdf), - et les mathématiques, c’est pas un métalangage, c’est une système d’écriture qui permet de corriger l’objet, alors où est ce que Lacan nous dit ça ? Les mathématiques c’est écrit et la théorie des ensembles et l’écriture mathématique permettent de corriger l’objet ! Pas le sujet ! dans la psychanalyse on ne corrige pas le sujet, car il est incorrigible, pour une bonne raison c’est que c’est le sujet de la parole, et que celui qui parle il est jamais à l’abri d’un lapsus , de dire des bêtises, on ne va pas corriger le sujet, le sujet il est incorrigible, par contre le sujet il est invité à corriger son objet et à construire cet objet qui lui permet de s’orienter dans le symbolique comme avec une boussole, cet objet c’est ce qui s’appelle l’objet a, c’est une lettre, donc l’écriture c’est pour corriger l’objet, la parole c’est pour déconner, parce que de toute façon ne ne peut pas maitriser la parole, |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
Noeuds logique & écriture Noeuds topologique & parole,
Fonction de l'énonciation, |
la fonction de l’énonciation ça ne se corrige pas, si je l’ai dit, je l’ai dit, je peux démentir, mais ça ne change rien au fait que ça été dit. Et vous voyez que la fonction de l’énonciation qui à mon avis est découverte par l’enfant au moment du trauma, quand les parents justement n’en tiennent pas compte, et bien c’est la fonction phallique, mais c’est pas la fonction imaginaire du phallus des animaux, dans la sexualité animale, c’est la fonction imaginaire du phallus symbolique, qui va redevenir génitale au moment du narcissisme, dans l’image du corps, dans l’image narcissique, cette fonction d’autorité, de puissance, cette fonction phallique de la parole va redevenir génitale avec la question des éléments en pointe dans la géométrie, les éléments en pointes nécessaires à créer une différence de notre image dans le miroir, image symétrique, et puis les organes érectibles, chez le mâle, alors les enfants ne sont pas complètement crétins, ils font des théories phalliques, mais dans toute la période qui est prégénitale, avant l’Œdipe, le phallus c’était la puissance érotique, JMV20150602, .pdf, - Deux approches dans Noeud : la description graphique du noeud et la plasticité nodale, - Le nœud déforme l'espace, ou encore l'espace déformé ou informé révèle le nœud. Révèle qu'il y a du nœud, soit de la contrainte souple, ordre sous l'aspect algébrique. Le nœud déforme un espace de lettres. Exemple de la chaîne de Whitehead en psychanalyse et en linguistique. Voir le rêve de Tchéou … « Il ne sut plus si c'était Tchéou rêvant qu'il était papillon ou un papillon rêvant qu'il était Tchéou. ..» Essaim p 62, 63 - Le nœud ou fausse chaîne où chaque rond se noue aux autres ronds sans emprunter le trou des autres ronds. Chaque rond n'entre dans le trou d'un autre rond qu'à en ressortir ensuite en suivant son trajet Essaim p 128. C'est la propriété borroméenne. - Partie nœud, partie coupure, est le composé des zones pleines traversées par la coupure et des croisements par où passe la coupure. Cette partie peut présenter plusieurs composants. Np76 - Partie non-nœud, partie non-coupure, est le composé des pleins monochromes et des croisements par où ne passe pas la coupure. Elle peut présenter plusieurs composants. Np76 |
|
||||||||||||||||||||||||||||||||||||||||||||
| Noeudrondlogie, | ✔ | - in GP, - Projet, - des ronds, |
||||||||||||||||||||||||||||||||||||||||||||
Noeud borroméen & Chainoeud ! Docte-noeud !) |
✔ |
- noeud générateur, 3333-3333, .pdf, .swf; transformations du Bo aux 2Ch aux Noeuds propres, - le "docte noeud", essais, - Métaphore impropre du Nom du père, - approche , - Nouage, - Seule la famille des noeuds borroméens purs impropres, (faits et défaits par des mouvements noeuds impropre Ni, nous assure de l'homogénéité recherchée, géométrique, nodale, des trois ronds. Ceux qui y contredisent sont toujours des noeuds Bo généralisés. (La répétition en tant que lien, janvier-février 2012, JMV, TEE, Cours aux Mines). - Lacan veut utiliser le borroméen pour écrire la structure qu'il dit selon l'énoncé " il n'y a pas de rapport sexuel". Cette négation du rapport est d'une structure équivalente à l'impossiblité de distinguer d'entre les trois ronds qui tient les deux autres. Comme l'inversion d'une dimension dans le miroir, mais on ne sait pas laquelle. Chaque rond est banal et exceptionel. - comment le nœud borroméen agit dans le mouvement nœud ?; question intéressante, ce mouvement il ajoute un nœud, ou il retranche un nœud, un nœud borroméen, c’est pour ça qu’ensuite on va parler du nombre de nœud, le nœud borroméen il a Un nœud, on peut faire un mouvement nœud dans n’importe lequel de ses Triskels, et il se défait toujours avec un seul mouvement nœud, le nombre de nœud, c’est le plus petit nombre de mouvements nœuds, qu’il faut faire pour défaire ou faire un nœud, à partir de rond libre ou à partir d’une ficelle non nouée; JMV23092014, 02.05.40 - coupures dans le bo, - borroméen sur le triple tore, .swf, - presque pas noué (se défait pat 1 mouvement noeud) - Dans le nœud borroméen le nœud en tant que principe, en tant qu'ordre, par quoi toute la chaine-nœud subsiste ne réside pas dans un rond, mais y réside tout de même . Car à ôter un rond, les ronds de la chaîne sont libres . Il est faux que ce un quelconque soit le nœud, et il est faux qu'un quelconque ne le soit pas ! D'après Essaim p 130 - Borroméens augmentés et Lacan (relations entre) , swf, - entrelac brunien wiki, - Brunien, de Hermann Brunn, l'entrelac brunien le plus simple est le noeud borroméen.(Jablan.S.V, 1999), - De Brunn à Debrunner, - - ou chaine presque triviale de Milnor, (cité par JMV dans "ça claque", Essaim p 51) voir cour de JMV Joyce-Hamlet le Sinthome...du 13 février 2007. - - voir Milnor, - voir Borroméen, - Bo dans le discours de Lacan, - Les bos, |
||||||||||||||||||||||||||||||||||||||||||||
- Lacan veut utiliser le noeud pour écrire la structure qu'il dit selon l'énoncé : "il n'y a pas de rapport sexuel" L'équivalence s'homologue du non rapport, cette négation du rapport est une structure équivalente à l'impossiblité de distinguer d'entre les trois ronds celui qui tient les deux autres. Métaphore impropre, car il n'y a qu'un noeud où les trois ronds sont homogènes. Chaque rond est quelconque et exceptionnel, c'est la fonction paternelle. Banale et exceptionnelle. (ça claque, revue Essaim, JMV, p 54) - Chaine borroméenne de 3 noeuds de Trèfle, JMV leçon du 04 septembre 2007 |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
Noeud borroméen généralisé↑ |
✔ |
- La Topologie et le Temps, Lacan, Séminaire XXVI, 1978-1979, gaogoa, - le noeud borroméen généralisé, c'est une chaine d'un certain nombre de ronds dont la propiété est que si on retire un certain nombre de ronds, toujours le même, tout ce qui reste est libre ! JMV11092007, 22.48; - coupures dans le borroéen, |
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
Noeud borroméen fort généralisé ↑ |
✔ |
- - 4444-8554, Noeud borroméen fort généralisé, fantôme qui hante la nodalité. (" ça claque " Essaim, p 21) - Boforgé,( abréviation sur ce site), - le Boforgé ne se trouve que dans la théorie positive des modèles physiques, . Dans les autres théories (voir ci-dessus), il disparait dès la première ligne, par quatre mouvements noeuds (propre, ou hybride, ou impropre). JMV souligne l'emabarras que cela pose à la théorie positive des noeuds , dans le sens de l'échec des tentatives de faire correspondre des invariants algèbriques à ces objets topologiques. - " ça claque", revue Essaim, 2008, JMV, du noeud borroméen fort généralisé. Définition, fonction et champ de la généralisation, JM.Vappereau, 2008/2, n°21, p45-66 Essaim (Cairn info) - Généralisation du noeud borroméen, Lacan, la Topologie et le temps, SXXVI, 21 novembre 1978, |
||||||||||||||||||||||||||||||||||||||||||||
Noeud borroméen hyper généralisé ↑ |
✔ |
- 4444-7654, Noeud borroméen hyper généralisé. 18 c. - Hyperbogé (abréviation sur ce site) |
||||||||||||||||||||||||||||||||||||||||||||
Noeud borroméen 4 CH ↑ |
✔ |
- nouage par les incorporel(le)s.5554-12555, - TEE, |
||||||||||||||||||||||||||||||||||||||||||||
Noeud Chainoeud ↑ |
✔ |
- Noeud : Chaine et noeud, c'est une chaine mais sans enlacement ( ce qui est pourtant un caractéristique des chaines d'avoir au moins un enlacement!), donc c'est une chaine non enlacée, mais nouée, avec un noeud (cas du Noeud de Whitehead, du Noeud Borroméen) c'est le noeud qui fait tenir les ronds ensembles, et non un enlacement , |
||||||||||||||||||||||||||||||||||||||||||||
| Noeud chiral | ✔ | - un noeuds non équivalent à son image miroir est appelé noeud chiral (du grec chiros = main). in BAYER, cas du Trèfle, du Borroméen, il y a un noeud droit (Dextrogyre) et un noeud gauche (Lévogyre), |
||||||||||||||||||||||||||||||||||||||||||||
Noeud coupure |
✔ |
- Noeud coupure : Ce sont des noeuds alternés dont tous les croisements sont traversés par une coupure. Noeud p 167. ( C'est le cas du Trefle ou de la famile des Trèfles; du Borroméen pour la famille des chainoeuds Borroméens, ) - Coupures pour les noeuds propres et les chaines, gaogoa, - Trefle, pour les noeuds propres, |
||||||||||||||||||||||||||||||||||||||||||||
Noeud impropre, |
✔ |
- [cette expression vient de Conway, c’est pour dire nœud proprement dit, au sens où je ne crois pas tellement au sens propre des mots, Conway dit, les nœuds propres sont les nœuds faits d’un seul fil, et ] le nœud borroméen de Lacan c’est pas un nœud propre parce que c’est une chaine, il n’y a pas un fil, il y a 3 fils, donc ça j’appelle ça le nœud impropre, et ça permet aussi d’apprécier ce que Lacan dit de cette chaine borroméenne, le nœud borroméen c’est une métaphore impropre, JMV11092007, II-04.10 |
||||||||||||||||||||||||||||||||||||||||||||
Noeud de Lacan ↑ |
✔ |
- 3322-442, .pdf, |
||||||||||||||||||||||||||||||||||||||||||||
Noeud de Listing ↑ |
✔ |
- 332-332, .pdf, .swf, - Listing, thèse, - du noeud de Listing au noeud de Lacan.... |
||||||||||||||||||||||||||||||||||||||||||||
Noeud logique Noeud mathématique |
✔ |
- Noeud, Noeuds logiques, noeuds trivial, noeuds toplogiques, JMV02062015, .html,
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Noeud mathématique ou noeud logique |
✔ |
- voir noeud logique | ||||||||||||||||||||||||||||||||||||||||||||
Noeud (non)
(Non noeud) ↑ |
✔ |
- voir non-noeuds, - Théorie des non-noeuds, JMV - non noeuds toriques, chainettes alternées, chaines olympiques, |
||||||||||||||||||||||||||||||||||||||||||||
| Noeud premier | ✔ | - premier noeud premier, Noeud p45, Encore p111-113 - Table des 21 premiers noeuds premiers, : qui ne sont divisibles que par eux-même et le noeud trivial. |
||||||||||||||||||||||||||||||||||||||||||||
Noeud propre ↑ |
✔ |
- Table des noeuds propres dans la table de Rolfsen, |
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
Noeud (Pur) ↑ |
✔ |
- Un pur noeud est un objet tel que la coupure passe par tous les croisements (Noeuds, p117) |
||||||||||||||||||||||||||||||||||||||||||||
Noeud sans fin |
✔ |
- 3322/644, (.pdf, .swf), ou Noeud sans fin, ou Srivatsa de Vishnou, ou noeud de la compassion sans borne ou infinie du Bouddha, ou noeud de l'Amour, ou Rolfsen 74, ou Paillasson ....! | ||||||||||||||||||||||||||||||||||||||||||||
Noeud de Soury↑ |
✔ |
- 6433-6433, (.pdf, .swf) - le noeud de Soury est trivialisable par deux homotopies. ( selon moi 4 !? ) (Soury y voyait une objection au caractère fondamental du noeud borroméen, qui n'est pas trivialisable par homotopie.). (" ça claque ",JMV, p53) Hors ce noeud vient d'une chaîne borroméenne à quatre de la suite des borroméen, suite issue du premier prototype, le 3333, formant des chaînes étudiées par Finke, finkéennes ou dites aussi par Soury : Chainette borroméennes à homotopie près. JMV in " ça claque " p55 - Le noeud de Soury est un composé de deux noeuds borroméens généralisés dernière manière. in " ça claque ", p55, JMV, 2008 - Le noeud de Soury grace au noeud borroméen généralisé reste dans la famille engendrée par le borroméen prototype. p55. - Chaines et noeuds,P. Soury, M.Thomé. |
||||||||||||||||||||||||||||||||||||||||||||
| Noeuds (Tables de) ↑ | ✔ |
- Table de Rolfsen (Noeuds propres, 2 Chaînes, 3 Chaînes), par nombre de croisements et ordre et ici , |
||||||||||||||||||||||||||||||||||||||||||||
Noeuds ( Théorie des ) |
✔ |
- Théorie des noeuds propres, voir cours JMV de juin 2014 sur TEE - sur wiki - Bibliographie, entête de cette page, - voir Théorie des noeuds, ci-dessous, - voir Noeud topologique, |
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
Noeud topologique |
✔ |
- Un noeud topologique est un plongement du noeud trivial. Le noeud trivial c'est le cercle trigonométrique défini de manière analytique sur le plan par l'équation à deux variables celui du " pont aux ânes" classique (x2 + y2 = 1), mais en abandonnant l'invariant euclidien de la mesure pour priviliégier la différence de la topologie définie par le couple : continu ou discret : connexe ou non connexe (coupé). Ce noeud ... (voir noeud logique) - Pour les noeuds topologiques, on ne s’occupe pas des ronds et des ellipses, de la géométrie analytique, on va appeler ça des ronds de ficelles. L’intérêt d’appeler ça rond de ficelle c’est qu’on ne précise pas trop ce qu’est la déformation, mais on sait que c’est une déformation continue, c’est un rond avec de la corde et puis une épissure, et on a un rond de ficelle qu’on peut déformer autant qu’on veut ! Et donc voila les nœuds topologiques qui sont connus. Alors qu’est ce qui est intéressant dans le nœud topologique, c’est que la connaissance du rond de ficelle, la connaissance du cercle ou des ellipses, ou même les déformations topologiques continues des cercles, et bien on connait ça très bien maintenant, mais c’est pas pour ça autant qu’on a une théorie des nœuds ! ça contredit et ça répond d’une manière négative à la question de Leibniz, le fait de connaitre la structure interne d’un objet, permet de connaitre toutes les situations de cet objet plongé dans un espace de plus grande dimension ! De la théorie des nœuds, l’idéologie de l’hégémonie alphabétique et numérique. Pour une autre écriture, et une autre lecture… (d’autres langues non alphabétiques, des rêves.. des nœuds..) Voilà les nœuds topologiques et on voit bien qu’il n’y a pas de théorie des nœuds, les mathématiciens s’acharnent encore aujourd’hui à associer à chaque nœud et à chaque chaine un polynôme pour essayer de ramener ça aux nombres, puisque les nombres c’est le développement de l’écriture par position, du système d’écriture des nombres par position, qui donne les polynômes, et on cherche à les associer aux nœuds, et même des polynômes, jusqu’à Alexander et Kaufmann, Homfly dans les années 80, ça c’est des choses que Lacan n’a pas connu, le polynôme de Homfly, celui de Kaufmann, je parle de ça dans l’annexe de Nœud, et justement ma position par rapport aux nœuds, c’est pas du tout de les ramener à des nombres, et des choses connues, il y a cette espèce d’hégémonie, dans la langue c’est une hégémonie alphabétique, et dans les mathématiques c’est une hégémonie numérique, donc métrique, la topologie est considérée, même quand on fait des programmes d’études des espaces topologiques, on peut lire dans certains institut qu’on étudie la topologie des espaces normés, des espaces de Hilbert normés, c’est pas la peine de parler de topologie s’ils sont normés, ils ont des mesures, ils ne sont pas spécialement topologiques, et il y a même un professeur éminent qui a dit que la topologie en géométrie algébrique, .. ?, ça ne servait à rien, 09.30 , et oui justement c’est pour ça que ça nous intéresse, parce que ça sort des considérations numériques, et métriques, la topologie ne s’intéresse qu’aux relations d’ordre. Et ça rend ces objets et cette topologie difficile à lire, mais c’est pas parce qu’elle est difficile à lire qu’elle nous intéresse mais c’est parce qu’elle sort de ces soit disant facilité qui sont finalement des à priori tout à fait idéologiques, moi je tiens que l’écriture des nombres par position qui est effectivement parfaite au sens où chaque nombre a une seule écriture, une seule expression, il n’y a pas de double, et n’y a pas d’omission, on peut construire tous les ordinaux à partit des axiomes de Penao, ...JMV20150602 - JMV20150602, p9... - le nœud ça commence avec cette histoire de narcissisme, c’est une tension subjective entre une position du sujet qui est intrinsèque et une position qui est extrinsèque, dans le champ scopique pour le miroir et c’est vrai aussi pour la voix. Seulement les oreilles ne se ferment pas alors on est pas tout à fait dans la même situation que dans le champ scopique, et cette différence, la voix c’est la même chose que le regard, c’est des choses où il est question de cette différence à propos de l’objet ! La répétition, le rêve et le cauchemar, Cette différence du phonème, cette différence du nœud, cette différence narcissique, Freud va la redécouvrir sous le nom de la répétition, ce qui fait que personne ne pige rien de ce qu’on a traduit par au-delà, de l’autre côté du principe du plaisir, et il s’agit dans la répétition pour Freud de s’apercevoir que dans les rêves le désir, c’est la relation, le désir s’est réalisé dans un rêve, le rêve c’est la réalisation d’un désir, mais c’est pas le plaisir, il y a le plaisir qui gouverne le processus primaire, mais le rêve peut même le contredire, la preuve, c’est qu’il y a des cauchemars, c’est ce que se croit Popper autorisé dans les annexes de son ouvrage sur la Logique de la recherche scientifique, ça s’appelle Postscriptum ; et là toute une partie de Postscriptum est consacrée à la destruction de Freud, qui serait soit disant vérificationniste, que Freud ne pratiquerait pas l’invalidation de ses théories, comme Popper propose que ça se passe en Science, la falsification, alors que Freud justement il cherche à falsifier sa théorie du rêve, 30.35, il s’aperçoit qu’il y a problème, mais il est entrainé dans cette logique que nous allons découvrir avec les nœuds logiques, - voir MP3 cours janvier février JMV 2015, et Textes, ; Et - juin 2015, argument. |
||||||||||||||||||||||||||||||||||||||||||||
Noeud de Trèfle ↑ |
✔ |
- 222-33 - premier noeud premier, Np45, Encore p111-113 , - Noeud torique, de la famille des trèfles, p165, Noeud, JMV, noeud coupure, - le noeud de trèfles, éléments .... - Noeud propre, (plus petit noeud), - une étude sur le noeud de trèfle de E.BAYER-FLUCKIGER, |
||||||||||||||||||||||||||||||||||||||||||||
Noeud trivial |
✔ |
- Le noeud trivial des mathématiciens, un cercle, dans la logique courante, ou LCC, Logique Canonique Classique ( L2T2) dominé par la Loi de la parole : Impératif du dire et fonction du phallus symbolique. Injonction de la Vérité de la moindre énonciation ( dire, c'est dire la vérité,( vrai ou faux, c'est toujours vrai !) ). "La fonction imaginaire du phallus symbolique" ne connait que deux constantes notée 0 et 1. | ||||||||||||||||||||||||||||||||||||||||||||
Noeud de Whitehead ↑ |
✔ |
- 3222-433, .pdf, .swf, - le noeud de Whitehead, éléments, et lire ce même item avec des compléments dans PIANOEUDS, - Le noeud de Whitehead, est une chaine (de 2 ronds ici,) , un chainoeud, tenant par 1 noeud, comme le borroméen, il se défait par 1 mouvement noeud, - Une relation entre le Whitehead et les termes de la formule du fantasme, ... JMV 11 février 2014, |
||||||||||||||||||||||||||||||||||||||||||||
Nombres ↑ |
✔ |
- Il y a des centaines de systèmes de numération, qui reposent tous sur les parties du corps, ... des arabes et des indiens nous héritons de leurs chiffres, c'est-à-dire des lettres qui écrivent les nombres, et du coup on croit que ça va donner une écriture, l'écriture alphabétique c'est un délire ... |
||||||||||||||||||||||||||||||||||||||||||||
Nombres, |
Théorie des nombres, W, Ensemble de nombres W, |
|||||||||||||||||||||||||||||||||||||||||||||
| 1, .pdf, | ||||||||||||||||||||||||||||||||||||||||||||||
| Encodage des caratères spéciaux, outils javascript, caractères scientifiques, |
N ajouré : Z ajouré : Q ajouré : R ajouré : C ajouré |
: |
||||||||||||||||||||||||||||||||||||||||||||
| Encodage des caratères spéciaux, outils javascript, caractères scientifiques, .jpg --> ci-contre
ci-dessous pour le code à insérer, ne pas considérer les antislashs (\) de début et fin de phrase ! |
N ajouré : |
|||||||||||||||||||||||||||||||||||||||||||||
| Z ajouré : |
||||||||||||||||||||||||||||||||||||||||||||||
| Q ajouré : |
||||||||||||||||||||||||||||||||||||||||||||||
| R ajouré : |
||||||||||||||||||||||||||||||||||||||||||||||
| C ajouré : |
||||||||||||||||||||||||||||||||||||||||||||||
\<td id="encode-cara-92" class="notranslate valeurnex"> <span class="wdg-select-all">ℕ</td>\, ENTIERS NATURELS |
N ajouré : ℕ | |||||||||||||||||||||||||||||||||||||||||||||
| \<td id="encode-cara-100" class="notranslate valeurnex"><span class="wdg-select-all">ℤ</td>\, ENTIERS RELATIFS | Z ajouré : ℤ | |||||||||||||||||||||||||||||||||||||||||||||
| \<td id="encode-cara-95" class="notranslate valeurnex"> <span class="wdg-select-all">ℚ</td>\, NOMBRES RATIONNELS | Q ajouré : ℚ | |||||||||||||||||||||||||||||||||||||||||||||
| \<td id="encode-cara-96" class="notranslate valeurnex"> <span class="wdg-select-all">ℝ</td>\, NOMBRES REELS | R ajouré : ℝ | |||||||||||||||||||||||||||||||||||||||||||||
\<td id="encode-cara-69" class="notranslate valeurnex"><span class="wdg-select-all">ℂ</td>\, NOMBRES COMPLEXES |
C ajouré : ℂ | |||||||||||||||||||||||||||||||||||||||||||||
Nombre d'enlacement |
✔ |
- dans l’ouvrage Nœud, je montre qu’on peut faire des mouvements nœuds pour arriver au nombre d’enlacement, de la figure du nœud, parce que si c’est une chaine, il y a des enlacements, et il y a un truc connu des mathématiciens, qui s’appelle le Nombre d’enlacement, on peut parvenir à construire la chaine sans nœuds, qui serait la chaine de pur enlacement, le pur non nœud contenu dans le nœud, JMV23092014, 2.07.00, .html, Miroir des formants, | ||||||||||||||||||||||||||||||||||||||||||||
Nombre d'or |
✔ |
- voir Fibonacci, - voir Or, ci-dessous, |
||||||||||||||||||||||||||||||||||||||||||||
Nombre de noeud |
✔ |
- le nombre de nœud, c’est le plus petit nombre de mouvements nœuds, qu’il faut faire pour défaire ou faire un nœud, à partir de rond libre ou à partir d’une ficelle non nouée. | ||||||||||||||||||||||||||||||||||||||||||||
Nombre pair nombre impair |
✔ |
Définition des nombres pairs et impairs, je vous ai dit que 0 et 1 c’est la congruence modulo 2, donc c’est les nombres pairs et les nombre impairs, 0 c’est tous les nombres pairs, et 1 c’est tous les nombres impairs, donc si vous prenez 2 nombres impairs, 1+1 = 0, vous voyez bien que la somme de 2 nombres impairs ce sera toujours pair ! parce que une nombre impair c’est toujours une nombre pair plus ou moins un, un nombre impair on va l’appeler 2k +1, et un nombre pair on va l’appeler simplement 2k, c’est un multiple de 2, (V02-12.40) ; JMV20150602, |
||||||||||||||||||||||||||||||||||||||||||||
Nombres cardinaux et nombres ordinaux ↑ |
✔ |
- Cardinal, de cardo, gong, pivot : En linguistique , les nombres entiers naturels zéro , un , deux , trois , etc. s'appellent des adjectifs numéraux cardinaux . En mathématiques , un nombre cardinal est une extension de cette notion pour dénombrer les ensembles, y compris des ensembles infinis . Le cardinal d'un ensemble fini E est le nombre d'éléments de cet ensemble noté Card E. (Wiki et Dedelicq) - Ordinal : En mathématiques , on appelle nombre ordinal un objet permettant de caractériser le type d'ordre d'un ensemble bien ordonné quelconque. Comme, en linguistique , les mots premier , deuxième , troisième , quatrième , etc. s'appellent des adjectifs numéraux ordinaux , et servent à préciser le rang d'un objet dans une collection, ou l'ordre d'un événement dans une succession. Georg Cantor a été amené (lors de ses travaux sur les séries trigonométriques ) à nommer de même le concept qu'il avait introduit à cette occasion pour caractériser le type d'ordre des ensembles qu'il rencontrait, de façon plus précise qu'en les mesurant par leur cardinalité (leur « nombre d'éléments »). Les ordinaux finis peuvent en fait être identifiés aux entiers naturels qui s'identifient eux-mêmes aux cardinaux finis, mais, dans le cas des ensembles infinis, ce n'est plus vrai : tous les cardinaux sont encore identifiables à des ordinaux, mais la réciproque est fausse. (Wiki) |
||||||||||||||||||||||||||||||||||||||||||||
Nombre de la coupure k ↑ |
✔ |
: la coupure passe par un certain nombre de demi torsion, ce nombre est le nombre de la coupure noté k, Np78 |
||||||||||||||||||||||||||||||||||||||||||||
Nombre de chaîne ↑ |
✔ |
- le nombre de chaîne d'un objet X, noté ch (X), est égale à la demi somme des valeurs caractéristiques des croisements impropres de X, et indique le nombre d'enlacement ! Algorithme de lecture des nœuds et des chaînes de 3 ronds par les coloriages : Pour deux ronds ; le répartitoire se résume à 1 chiffre ∑= ch (C), il y a deux chaines possibles pur chaque nombre entier, positif ou négatif. Pour un rond, la réduction du répartitoire se résume au chiffre zéro ∑ = 0 Pour quatre ronds et plus : voir page 5 et suivantes …. |
||||||||||||||||||||||||||||||||||||||||||||
Noms du père |
✔ |
- Le nom du père, lien au Triskel, au Trait unaire, à l'identification, - Les noms du père , c'est ce que l'étranger ne peut pas comprendre et qui est désigné par la mère à l'enfant comme désirable chez le père. Il y a des noms du père, familiaux, dans votre appartenance à un quartier, à un club, à une région, à une nation. Ce sont des traits différentiels, des marqueurs, non nécessairement marqués, mais que seuls certains sujets savent lire ! Ce sont les prémisses des causes, des idéaux, et des guerres.... - voir Manuel d'etnographie de Marcel Mauss, sur UCAQ, et ici, Table des matières |
||||||||||||||||||||||||||||||||||||||||||||
| - Les Nom du Père, séance du 20 novembre 1963, LACAN, version Espace-Lacan, et sur gaogoa, - Les non-dupes errent, Séminaire XXI, 1973-1974, LACAN, sur gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||||
Non-être |
✔ |
- - du non-être, Que suis-Je, - voir Vide, Hénologie, Incorporels, 2, 3, |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Non-nœud ↑ |
✔ |
- pour une théorie des non-noeuds, JMV - Géométrie des non-nœuds : géométrie au sens de Félix Klein, catégorie dit-on aujourd'hui. Définie par Conséquences : |
||||||||||||||||||||||||||||||||||||||||||||
| Nouage | ✔ | - Des surfaces au noeud....1, 2, 3, - Du croisement, au triskel, au Trèfle, le mouvement Noeud, puis le Borroméen, gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
- Il y a une rupture structurale entre les chaines à 3 et les chaines à 4 ronds. Jusqu'à 3 ronds la topologie des chaines est engendrée dans une certaine continuité. Au delà c'est la discontinuité qui domine. D'où l'importance des coupures ... - Nouage du graphe de ligne du schéma de la lettre 52 dans le schéma F puis L : La perception et la consience nouées en travers de ce schéma, cette structure, nous défait des prétentions génétiques et évolutionnistes, avec les prétendus stades. - le nouage et l'enlacement s'efface dans le passage à l'intrinsèque, laissant une trace, sous l'aspect de ces caractéristiques, de ce qu'il y a du nœud, de la chaine Np69 |
||||||||||||||||||||||||||||||||||||||||||||||
Nouage du bord ↑ |
✔ |
- Enlacement (et nouage du bord) , ils définissent les caractéristiques de surface de l'étoffe, convenant ainsi à la structure de la pulsion (drive, trieb) décrite par Freud, où la constance de la poussée (invariance du groupe fondamental, voir Essaim), est raccordée à la source par l'intermédiaire de son bord (prévalence des orifices corporels, érogénisation par le langage). Np69 |
||||||||||||||||||||||||||||||||||||||||||||
Nosographie, ↑ |
✔ |
- voir Clinique, Structure, Théorie de l'asile, - Voir Identifications sexuées et Structure Freudo lacanienne du symptôme, gaogoa, - voir PIANOEUDS, |
||||||||||||||||||||||||||||||||||||||||||||
Notation |
-
La notation un, dite indicielle est due à Lagrange : n est placé en indice , par opposition à la notation exponentielle où n serait placé en exposant : un; signifiant u puissance n lorsque u désigne un nombre. Dans notre exemple, pour désigner 1 - 1/n, plutôt que de parler de l'image de n, on parlera de terme général . (Melh, Suites) |
|||||||||||||||||||||||||||||||||||||||||||||
| O | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
| objet (a) | ✔ |
- L'objet a est éclaté, mais lisible, il est diffracté, divisé ... où ? ( c'est le mécanisme commun et basique de la psychose, qui détruit l'objet a dans le noeud borroméen produisant le noeud de trèfle ! Perte de la lisibilité ! ) - l'objet a, Lacan l'identifie à la pastille sphérique, voir l'Etourdit, pastille bilatère. - l'objet du sujet peut être corrigé, par l'écriture du sujet, sans adapter ou suturer ou corriger ce dernier. Le sujet ne se corrige pas, l'objet oui ! |
||||||||||||||||||||||||||||||||||||||||||||
Optique géométrique |
✔ |
- Stade du miroir : le stade du miroir comme formateur de la fonction du Je, Ecrits p91, Lacan, - Remarques sur le rapport de Daniel Lagache, p673, 674, 680, Ecrits, lacan, - Deux aspects géométriques du narcissisme, JMV 17 mai 2011 - |
||||||||||||||||||||||||||||||||||||||||||||
Or (nombre d') |
✔ |
- Nombre d'or et section dorée, Mehl, NEVEUX.Marguerite, HUNTLEY.H.E, Le nombre d'or, Radiographie d'un mythe suivie de la Divine proportion, 1995, Sciences, Points, Seuil, sur gaogoa, WARUSFEL André, Les nombres et leurs mystères, Points, Sciences, Seuil, 1961, sur gaogoa, sur le nombre d'or, ...p98, |
||||||||||||||||||||||||||||||||||||||||||||
Organisme |
✔ |
- ce qui caractérise l'organisme, selon Canguilhem, c'est la Persévérance ! in Machine et organisme, - les organismes fabriquent des monstres... in Le monstrueux et la monstruosité. - Machine et organisme, JMV16062015, |
||||||||||||||||||||||||||||||||||||||||||||
| Ouvert | ✔ | - Intuitivement, un ouvert correspond à un ensemble qui ne contient pas sa « frontière ». - En mathématiques et plus particulièrement en topologie générale, un ensemble ouvert, aussi appelé une partie ouverte ou, plus fréquemment, un ouvert, est un sous-ensemble d'un espace topologique qui ne contient aucun point de sa frontière. L'ouvert est l'élément de base d'un espace topologique. ....
|
||||||||||||||||||||||||||||||||||||||||||||
| P | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
p |
✔ |
- variable pour la logique | ||||||||||||||||||||||||||||||||||||||||||||
Paradoxes |
✔ |
- - paradoxes, |
||||||||||||||||||||||||||||||||||||||||||||
Paranoïa↑
|
✔ |
- le Paranoïaque ne supporte pas les Juifs et les Homosexuels, parce que c'est pas écrit dessus ! ( Est-il nécessaire que ces derniers hystérises cette demande des paranoïaques ?, Quid de la "visibilité" ? De la Com ? Paraître ?. C'est une question ?). Ce sont les antisémites et les homophobes ! Destruction de la lisibilité ! Mise en continuité des consistances RSI, du noeud Borroméen, pour le réduire au Trèfle.... Les porteurs de traits explicites font l'objet de ségrégation, pour les traits non marqués ils font l'objet de persécution... Le mécanisme paranoïaque est commun à tous, ( défaut de lecture) avec plus ou moins d'intensité, mais sa conjugaison avec les facteurs de la Folie, articulent la Personnalité paranoïaque folle. La paranoïa c'est la Personnalité, dira Lacan, voir sa thèse.. Il est possible d'atténuer "sa" propre paranoïa en apprenant à lire, c'est l'objet de la psychanalyse .... lire le non marqué .., devenir un peut moins paranoïaque et un peu moins fou ... c'est un programme ....! ( voir Id sexuées, et structure freudienne du symptome, et folie) De nombreuses Personnalités sont au pouvoir ! Par la force, par l'abu de pouvoir, autoproclamées, ou par les urnes, c'est la force des démagogues, qui par la force de leurs rhétoriques séduisantes et sommaire, entrainent les populations dans des aventures dont elles ne se relèvent pas ! - la foclusion c'est la forclusion de la lisibilité, JMV20150602 - le noeud de Trèfle (Noeud propre) - le noeud de Trèfle, (destruction d'un Triskel du noeud Borromée) - les formes de la paronoïa, Dali 1, 2, 3; Aimée, 1, 2, ; Schreber, 1,2, 3; Papin, 1, 2, ; Massacres et Persécutions (AuswBirkHiroNagaArmTcherRwanShrebrenFuku....) oeuvres de Personnalités ...Hitler, Mladic, Truman, ... - Nouvelle psychose paranoïaque, - Illustration, - voir psychose, - voir Surréalisme, |
||||||||||||||||||||||||||||||||||||||||||||
Pari de Pascal |
✔ |
- Lacan va faire des variations autour du nombre d’or qui sont assez amusantes, 33.26, ça c’est particulièrement dans son étude du pari de Pascal, et dans un Autre à l’autre, mais il y revient assez souvent et là avec les Suites de Fibonacci, il a mis beaucoup de temps à étudier ça, j’ai déjà fait remarquer que Lacan commence à parler du Pari de Pascal dans le Séminaire qui s’appelle l’Objet de la psychanalyse, il donne ses sources, il cite Brunet..JMV2092014,33.26 - voir Fibonacci, |
||||||||||||||||||||||||||||||||||||||||||||
| Parité de la coupure↑ | ✔ |
- c'est le caractère pair ou impair du nombre de la coupure, noté k (Noeud p103-104) si la coupure est impaire le nœud alterné est de la famille des Trèfles si la coupure est pair, le nœud alterné est de la famille de Listing, Np79 -Parité de la coupure : -fixe pour les chaines faites de plusieurs ronds, -fixée pour les nœuds propres et les chaines ayant une surface d'empan minimale, et une seul (nœud et chaines non équilibrées ! P>V) -fixe pour les nœuds propres et les chaines équilibrés (P = V) Np81 |
||||||||||||||||||||||||||||||||||||||||||||
Parole↑ |
✔ |
- Parole, - La parole c'est le Symbolique, mais dans la langue et avec l'énonciation, ça n'est pas détaché du mimétisme animal, mais dans la Langue, - la parole c'est continue et que ça dit la vérité, alors que l'écriture est discrète et produit du savoir, c'est à cette occasion là qu'on parle du savoir, qui n'est pas la connaissance, ce n'est pas non plus un savoir faire, c'est un savoir lire, savoir écrire, savoir compter, le savoir ça commence avec la différence entre l'écrit et la parole, JMV09092014, - c'est le fait de dire, c'est l'Autorité, et la Vérité, dire, c'est dire la Vérité, - dans la parole on se trompe tout le temps, c'est les embrouilles du vrai ! - DI (ou la Dei)=trauma=le Phallus=la Parole=fonction phallique - Parole et inconscient , partie III, in Eros et psyche, JMV - Parole-Ecrit, - Donc voilà, vous voyez bien qu’on peut étudier les phénomènes de discontinuité, et de coupure et de collure, en utilisant les moyens de la topologie, qui est une discipline qui est réputée étudier les propriétés invariantes des fonctions continues, donc ça c’est une petite réflexion pour définir ce qui s’appelle Topologie, ce que fait Lacan dans l’Étourdit à propos du tore et de la bande de moebius, ça semble contredire la définition de la topologie, et pourtant c’est parfaitement légitime d’utiliser cette topologie pour parler de cette discontinuité, parce que la topologie elle étudie le continu !, c’est quand même une façon intéressante de réfléchir à cette obstruction disons discursive, qui fait que si on pratique disons une discipline qui étudie la continuité et les invariants des fonctions continus, on s’interdit de s’intéresser à des choses discontinues, hors l’important c’est pas de s’interdire de parler des choses discontinues, l’important c’est de pas les mélanger, c’est de faire la différence entre ce qui est continu et ce qui est discontinu, à chaque étape, et ça semble plus difficile et même hors de porté à certains, voyez c’est le côté provoquant de Lacan qui va donc utiliser la topologie pour étudier des phénomènes qui nous intéressent dans la psychanalyse et qui sont donc pas continus, le premier lieu où se situe la différence entre le continu et le discontinu, c’est la parole et l’écriture, et c’est ce qui distingue la parole de l’écriture, ..... L’écriture Introduit la discontinuité dans le continu, hors il se trouve que ça fonctionne très bien avec le phonème, qui est d’abord parlé, ce que Lacan appelle le Signifiant, et moi je vous propose de parler du phonème dans la psychanalyse avec Lacan en terme de Signifiant pour ce qui est du côté des oreilles, dans ce qui s’entend, et de parler du phonème dans ce qui s’écrit et qui s’appelle la Lettre chez Lacan, vous avez ça dans l’Instance de la lettre, Lacan parle, au moment ou Lacan introduit l’algorithme Saussurien, le S/s, il parle de la chaine signifiante et il dit, et il parle de l’élément différentiel dernier qui est la Lettre et qu’on appelle phonème, !!, alors voyez là, il emploie le mot phonème pour la lettre ! et même le mot phonème pour le lettre et le mot lettre pour le phonème, donc moi je pense que le phonème des linguistes, il y a le phonème dans la langue parlée, du locuteur, dans la langue vulgaire, dans la langue de celui qui parle de manière plus ou moins continue, dans le flux verbal qu’on ne comprend pas si on ne le découpe soit même, donc écouter quelqu’un ou lire, c’est découper, c’est introduire ce que Freud appelait dès les Etudes sur l’aphasie, les verneinugzeichen, voyez dans les schémas de Freud, vous avez Verneinung et Verneinungzeichen, vous avez perception et perception-signe , JMV1606015, - dans la parole et dans l’Écrit, mais c’est deux ordres absolument différent, l’un n’est pas le duplicate de l’autre, ça il faut absolument s’imprégner de cette notion JMV16062015, - les énoncés parlés c’est des assertions, c’est 1, c’est toujours Vrai, c’est même V sans u(Faux), la fonction phallique, la fonction phallique, l’impératif de la parole, l’énonciation, la loi de la parole, dont Lacan nous dit que c’est ce que rencontre Moïse en descendant du Sinaï, il entend une rumeur et il nous dit que C’est la loi de la parole, lui il descend avec des Lois écrites que lui a dictées Dieu, parce que n’oubliez pas, Dieu ne sait pas écrire, donc c’est Moïse qui a du les graver les Lois en question, c’est les Lois de la Parole nous dit Lacan, JMV20150602, .html, |
||||||||||||||||||||||||||||||||||||||||||||
Pentagramme |
✔ |
- Pentagramme étoile, 222-55, ( Discours tenus...) | ||||||||||||||||||||||||||||||||||||||||||||
Perception signe,
|
✔ |
- le propre de l'écriture c'est justement de découper, la lecture et l'écriture c'est de la découpe , et vous avez ça dès les premières pages de Freud, 0.32.44, et vous avez ça dès les premières pages de Freud sur les Aphasies, tout de suite il fait la distinction entre les perceptions et les perceptions signes, c'est là que porte Lacan la question de la Bejahung , (jugement d'attribution, jugement primaire), et de la forclusion quand ça ne marche pas, donc qu'est ce que c'est que les perceptions signes, les Wahrnehmungsbewußtsein c'est des perceptions découpées, c'est pas des signes de perception, des perceptions qui deviennent signes du fait d'un découpage, lire c'est commencer par découper (JMV09092014) - lire c’est apprendre à découper d’abord, donc là c’est une question de découpage, chez Freud c’est la das Wahrnehmungsbewußtsein, chez Lacan aussi, et moi je propose de traduire ça par Perception-signe, pas signe de perception, 1.26.50, c’est pas des signes qui représentent la perception, c’est la perception elle-même, qui devient signe, du fait d’être isolée JMV23092014, |
||||||||||||||||||||||||||||||||||||||||||||
Permutation↑
|
✔ |
- voir Combinatoire - sur wiki, -Deux aspects géométriques du narcissisme, JMV 17 mai 2011 (permutations dans le cube) |
||||||||||||||||||||||||||||||||||||||||||||
Perversion↑
|
✔ |
- Atteindre la pudeur de l'autre, pour en accaper la volonté. Atteindre la subjectivité de l'autre pour en accaparer la volonté ! (Kant avec Sade) Perversion, fantasme, et langage ont des structures proches. - Fétiche, - voir Structure Freudiennes du Symptôme, - Structure, style, - à différencier du Pervers, de la Perversité, du sadisme, du Désirant, et encore plus de l'Homosexuel, du pédophile, du pédéraste.... et de la folie... ( on peut être un hétérosexuel ou un homosexuel pédophile non fou !- en tant que structure- = ne pas passer à l'acte !) - Toute sexualité humaine est foncièrement perverse. - sur les éléments en pointe du corps propre, restituer à la mère le phallus un instant perçu comme manquant - fait agir l'autre à son insu pour sa propre satisfaction - Clinique du processus du neuds, JMV, 12-12-2014, p41 |
||||||||||||||||||||||||||||||||||||||||||||
Phallique
(fonction) |
✔ |
- la formule de la vérité de Tarski, c’est la formule qui dit que : « La neige est blanche » est vrai, , si et seulement si la neige est blanche . » x est i(x) si x c’est égal à x ! « La neige est blanche » est vrai si et seulement si la neige est blanche, et en logique c’est pire encore, car vous allez avoir une phrase comme : « la neige est verte » est vrai, si et seulement si la neige est verte, mais alors vous allez me dire qu’il y a quelque chose qui ne va pas, car la neige est verte, c’est pas vrai, et oui justement comme la neige est verte c’est pas vrai, dire que la neige est verte, c’est pas vrai non plus, dire que la neige est verte est vrai c’est aussi faux que de dire la neige est verte, c’est donc égal, vous avez là une réflexion sur la fonction, le signe égal, la vérité, et donc cette fonction phallique, phi de x, j(x), j’attire votre attention sur le fait simple que l’enfant quand il dit, jusqu’à la découverte de la castration de la mère, à la fin de l’Œdipe, quand il découvre (doigt pointé sur le x de i(x) = x), quand il se rend compte dans le langage, que cette Loi de la vérité, elle fonctionne déjà dans la parole, voyez que ici quand il dit : ma mère elle n’a pas de phallus mais il est là quand même, parce que c’est la même chose, qu’il soit là, ou qu’il ne soit pas là, c’est ce que dit Hans à propos de sa petite sœur, elle n’a pas de fait pipi, alors il ne le dit pas bien le petit Hans, alors il dit : elle va grandir, il est là mais il va grandir, elle va devenir grande et il va devenir grand, et Freud d’ajouter, il n’a pas tort de petit garçon, puisqu’elle a un clitoris, et ça c’est justement l’ennui de ces structures de sexe ! V02-10.58, si on les rabats sur les organes génitaux et la sexualité on retombe, on retourne après avoir quitté le champ de l’imaginaire du corps, on ne va pas reprocher à Freud de revenir là, lui il est médecin, et évidemment pour lui c’est une interrogation, on lui doit tout ça, ( ) , mais vous voyez que justement c’est pas une affaire de clitoris ou de taille de l’organe, c’est une affaire de structure de la parole, alors voilà, dire que « la neige est blanche » ou dire que « la neige est verte », c’est le fait de dire qui fait que c’est vrai ou que c’est faux, et donc c’est lié à l’énonciation, donc vous avez bien la critique de Wittgenstein qui dit qu’on arrivera jamais à définir l’adéquation qui caractérise la vérité, V02-11.55 ; 01.16.43 ; pour la simple raison que dire que « la neige est blanche » est vrai, c’est du langage, et que la neige est blanche c’est la couleur de la neige, c’est un fait, et les faits n’entrent pas dans la langue, alors il y a un divorce et il n’y a pas d’adéquation possible, mais moi je vous propose d’entendre la définition de Tarski, à la manière de Frege, qui lui l’entend déjà mieux, ou l’entendait avant Wittgenstein encore mieux quand Frege dit qu’ « il ne sert à rien de dire que quelque chose est vrai, ça n’ajoute rien à la vérité de cette chose », justement ça ne sert à rien de dire que x est vrai, parce que cette fonction de la vérité, une fonction identique, i(x), ça n’ajoute rien à la vérité de cette chose qui est là ( x) mais qui est dite, ce que nous découvre la psychanalyse et l’insistance de Lacan à propos de : Qu’on dise reste oublié derrière ce qui se dit dans ce qui s’entend ; c’est que justement il insiste sur cette dimension que « la neige est blanche » est vrai , c’est un segment cité comme le dit Tarski dans son exposé, il le met entre guillemets, c’est donc une citation, pourquoi ? parce que ça vient à la place du sujet d’un prédicat : est vrai, donc « la neige est blanche » est vrai, c’est « la neige est blanche » c’est cité, c’est la mention, dit Tarski, la mention de « la neige est blanche » dire que c’est vrai, il met des guillemets et c’est là, c’est là-dessus que s’applique la fonction de vérité, si et seulement si la neige est blanche, mais là il faut considérer que la seconde occurrence de la neige est blanche, dans cette seconde occurrence, il ne s’agit pas du fait physique de la couleur de la neige, il s’agit de l’énonciation, si quelqu’un dit « la neige est blanche », c’est vrai, c’est ça l’énonciation ! et ça c’est la fonction de l’autorité de la parole, et de la fonction phallique, qui est la fonction de ce type d’autorité, qu’il ne faut pas rabattre trop vite sur les parties génitales |
||||||||||||||||||||||||||||||||||||||||||||
Phallus↑ |
✔ |
- pierre dressée, - Hermès, Priape, in BOZARS,-Sculptures-Statuaire- ... - comique, - champ de gravitation de l'Homme, - organe du défaut AE p324 La logique du fantasme, - Nombre d'Or, - SIBONI.J, |
||||||||||||||||||||||||||||||||||||||||||||
Phobie↑ |
✔ |
- Phobie : mécanisme en jeu dans la Névrose, pour les Perversions le mécanisme élabore un fétiche... - Identifications sexuées, gaogoa, - Le territoire de la phobie , 2008, JMV , |
||||||||||||||||||||||||||||||||||||||||||||
Phonèmes↑ |
✔ |
- le phonème, il se réalise en Signifiant, dans le son et en lettre dans le graphisme, et l’économie du graphisme, et l’économie du son, l’économie du signifiant, Lacan dit l’inertie, c’est le principe d’inertie = la structure du langage, l’inertie n’est pas la même - Liste des 36 phonèmes du français, 2, - Phonologie, - Linguistique, - Troubetzkoï Nikolaï , Principes de phonologie, sur gaogoa et Langage, - L’écriture Introduit la discontinuité dans le continu, hors il se trouve que ça fonctionne très bien avec le phonème, qui est d’abord parlé, ce que Lacan appelle le Signifiant, et moi je vous propose de parler du phonème dans la psychanalyse avec Lacan en terme de Signifiant pour ce qui est du côté des oreilles, dans ce qui s’entend, et de parler du phonème dans ce qui s’écrit et qui s’appelle la Lettre chez Lacan, vous avez ça dans l’Instance de la lettre, Lacan parle, au moment ou Lacan introduit l’algorithme Saussurien, le S/s, il parle de la chaine signifiante et il dit, et il parle de l’élément différentiel dernier qui est la Lettre et qu’on appelle phonème, !!, alors voyez là, il emploie le mot phonème pour la lettre ! et même le mot phonème pour la lettre et le mot lettre pour le phonème, donc moi je pense que le phonème des linguistes, il y a le phonème dans la langue parlée, du locuteur, dans la langue vulgaire, dans la langue de celui qui parle de manière plus ou moins continue, dans le flux verbal qu’on ne comprend pas si on ne le découpe soit même, donc écouter quelqu’un ou lire, c’est découper, c’est introduire ce que Freud appelait dès les Etudes sur l’aphasie, les verneinugzeichen, voyez dans les schémas de Freud, vous avez Verneinung et Verneinungzeichen, vous avez perception et perception-signe . JMV16062015 |
||||||||||||||||||||||||||||||||||||||||||||
Phonétique↑
|
✔ |
- 118 PHONES ou SONS, ou 1 son correspond à 1 symbole (lettre entre crochet :
[R]). Quand on représente les sons d'une langue, on se sert de l'Alphabet Phonétique International (API) - La phonétique est l'étude scientifique des sons du langage humain. Elle exclut les autres sons produits par les êtres humains, même s'ils servent parfois à communiquer (les toux, les râclements de gorge). Elle exclut aussi les sons non-humains. - la phonétique, - Linguistique, |
||||||||||||||||||||||||||||||||||||||||||||
Phonologie↑
|
✔ |
- 36 PHONEMES, 1 signe correspond à 1 PHONEME, soit 1 TRAIT différentiel soit 1 signifiant ! - C'est la phonologie qui est importante pour la psychanalyse car elle étudie les traits différentiels d'une langue, c'est l'opposition entre les signaux, entre les sons, les Signifiants, les oppositions siginificatives qui ont un sens, et non pas le signe Saussurien (S/s -Signifiant sur signifié) qui se résoud dans la réprésentation. Parole et écrit sont des systèmes d'opposition dans le langage - Liste des phonèmes du français, - Phonologie, - L'étude phonétique d'une langue peut se faire sans faire appel au sens. À la limite, on pourrait étudier les caractéristiques phonétiques d'une langue qu'on ne comprenait même pas. Par contre, la phonologie s'occupe de la fonction des sons dans la transmission d'un message. Il faut donc comprendre une langue pour faire de la phonologie. En d'autres termes, la phonologie recherche les différences de prononciation qui correspondent à des différences de sens, ce qu'on appelle des oppositions distinctives . Or, tous les changements de prononciation ne changent pas le sens. - Linguistique, |
||||||||||||||||||||||||||||||||||||||||||||
| Physique & Métaphysique, | ✔ | - - Sciences ... gaogoa, - DESCARTES ; Pensée & Etendue, ( Machine et organisme, CANGUILHEM) - Physique & Métaphysique, |
||||||||||||||||||||||||||||||||||||||||||||
Plan projectif↑ |
✔ |
- définition wiki, - Objet a et cross-cap, gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
Platon |
✔ |
- Timée, - Platon 2.0, |
||||||||||||||||||||||||||||||||||||||||||||
Plasticité nodale |
✔ |
- Plasticité nodale : , il y a d’autres mouvements nœuds, tous ces traits verts correspondent à toute une panoplie de mouvements nœuds qui sont, c’est ça qui est amusant, ça peut se traduire par une déformation graphique, un changement de la figure, qui est visible, qui est lisible à l’œil nu, mais là on découvre qu’il y a une raison plastique nodale derrière « chaque ?, ce ? » mouvement ? 2.04.18, et ça c’est pas trivial, donc vous avez bien la continuation de ce que j’ai fait dans Nœud, j’ai toujours à partir du chapitre IV ou V, je distingue dans chaque chapitre, description graphique et plasticité nodale, chaque chapitre est coupé en deux, jusqu’au chapitre VI, hein, une série de chapitre, IV, V, VI, ils sont coupés en deux, il y a toujours le point de vue graphique; JMV23092014, .html, Miroir des formants, |
||||||||||||||||||||||||||||||||||||||||||||
Plongement↑ |
✔ |
- Dans la théorie des noeuds, l'objet est un simple cercle placé dans l'espace euclidien de dimension trois . La manière dont est situé l'objet dans l'espace correspond usuellement à la notion de plongement (N, p14) - L'amour du tout, 3eme partie JMV, 1992, L1T1, L2T2 dans L3T3 - plongement c’est-à-dire qu’on met un objet dans un espace plus grand, et plongement ça veut dire que la transformation de l’objet initiale, le rond ou les ronds, on plonge dans l’espace la fonction mathématique qu’on emploie si elle est injective, si elle n’est pas injective, ça s’appelle pas un plongement, ça s’appelle une immersion. - dans l’immersion, un point peut être l’image de deux points distincts, ça veut dire qu’on peut faire se traverser les cordes, puisqu’au moment de la traversée, au moment ou une corde traverse une autre corde, il y a une moment ou deux points se confondent dans le croisement, il n’y a plus un dessus dessous mais il y a un croisement immergé, - voir injectif |
||||||||||||||||||||||||||||||||||||||||||||
| Pyramide de Ponzi | - Un système de Ponzi ou Pyramide de Ponzi est un montage financier frauduleux qui consiste à rémunérer les investissements des clients essentiellement par les fonds procurés par les nouveaux entrants. Si l'escroquerie n'est pas découverte, elle apparaît au grand jour au moment où elle s'écroule, c'est-à-dire quand les sommes procurées par les nouveaux entrants ne suffisent plus à couvrir les rémunérations des clients1. Elle tient son nom de Charles Ponzi qui est devenu célèbre après avoir mis en place une opération fondée sur ce principe à Boston dans les années 1920. W, | |||||||||||||||||||||||||||||||||||||||||||||
Poinçon↑ |
✔ |
- Poinçon du fantasme : articule aliénation et séparation, J-M.VAPPEREAU, - Le vel de l'aliénation construction effective de l'opérateur vel et son articulation commune en logique classique .JMV ( .pdf ) ,(B.A 28-05/24-07-2006) ,
- mardi 08 septembre 2009, la séparation enfin (.pdf) , - 19 janvier 2010, - in Le travail du noeud, chap VI de Noeud, J-M.VAPPEREAU |
||||||||||||||||||||||||||||||||||||||||||||
Point↑
|
✔ |
- voir le Séminaire le Sinthome, Seuil, p 81 et Gaogoa p5: Dans la partie centrale du noeud borroméen, Lacan place un point, qu'il difinit comme la notation réduite d'une corde qui passerait là, et sortirait de l'autre côté. C'est la figuration de la droite infinie, soit la réduction du tore, ou tout aussi bien un trou ! (un point en topologie est un trou !); Voir plus loin dans le séminaire : Point noir ! - Point et cercle, - Le Point, - du point à la ligne & Dimensions, .swf, .pdf, - Point hors ligne .... |
||||||||||||||||||||||||||||||||||||||||||||
Popper |
✔ |
- - voir JMV23092014,52.30, .html, 2,(le mur des formants) |
||||||||||||||||||||||||||||||||||||||||||||
Post |
✔ |
- POST, seulement en 1921, a montré que tout le système d’écriture des Principia en matière de connecteurs pouvait donner lieu à la construction d’une table de vérité, et c’est je trouve admirable de lire Post dans cette démonstration, dans son fameux article où il introduit les tables de vérité, la sémantique de la logique, parce que tant qu’il n’a pas démontré son théorème, il est en logique modifiée, voyez, moi je lis chez un mathématicien, qui va établir les choses, par une démonstration, par un théorème, tant que le théorème n’est pas démontré, on n’est pas sous le coup du théorème, on est dans des démonstrations qui sont extrêmement difficiles à suivre, parce que on ne sait pas très bien où on est !! Et on peut trouver des lieux, des espaces, des constructions, je parle d’espace, mais c’est une métaphore, on peut construire un système d’écriture qui est justement un système dans lequel on navigue avant d’avoir trivialisé ou réduit, par des théorèmes le domaine qu’on étudie, il faut bien voir, c’est exactement ce qu’il se passe avec les rêves ! JMV23062015, |
||||||||||||||||||||||||||||||||||||||||||||
Postulat↑
|
✔ |
- Principe premier non démontré. Terme tombé en désuétude, on lui préfère Axiome. Dedelicq 553 |
||||||||||||||||||||||||||||||||||||||||||||
| Postures Positions dans l'analyse |
✔ |
pour l'analysant : -Savasana : position (asana), du cadavre (Sava), allongé sur le divan ou -Utkatasana : posture de la chaise ( psychothérapie, face à face, ...), peut évoluer vers la chaise bouddhiste, voir le Gaja vadiru et en fin d'analyse la chaise de Bouddha !! - Hasta-Mudra (main et geste) : avant de sortir un Mudra gracieux vers votre porte-feuille ... -pour l'analyste : - Utkatasana peut convenir à toute situation (vigile ou somnolente) - Somnolence discrète (éviter les ronflements), - ... |
||||||||||||||||||||||||||||||||||||||||||||
Préconscient↑ |
✔ |
- Pcs, articule les processus primaire et secondaire (Lu, 4=3, p69) - voir Lettre 52, Freud, - voir Schémas L, F ..; Math et schema L, L1, L2, F, .swf, |
||||||||||||||||||||||||||||||||||||||||||||
Prédicat↑ |
✔ |
- voir Calcul des Prédicats, Proposition/Prédicat : - Prédicat de vérité, voir Tarski, voir Métalangage, Il convient de noter cependant que la logique du premier ordre ne contient aucune relation spécifique (comme telle relation d'ordre, d'inclusion ou d'égalité) ; en fait, il ne s'agit que d'étudier la façon dont on doit parler et raisonner avec les expressions du langage mathématique. En logique mathématique, lorsqu'un prédicat est lié à une expression, on dit qu'il exprime une propriété (telle que la propriété d'être une planète), et lorsqu'il est lié à deux ou plusieurs expressions, on dit qu'il exprime une relation (telle que la relation d'être plus grand).
Ceci permet de formuler des énoncés tels que « Tout x est P » et « Il existe un x tel que pour tout y, x entretient la relation R avec y » en symboles : « Tout x est gentil » et « Il existe un x tel que pour tout y , x est ami avec y », ∀ x gentil(x) et ∃ x ∀ y a m i s ( x , y ). Les formules logiques déduites de ce calcul des prédicats ont pour but de s'appliquer à n'importe quel modèle , c'est-à-dire n'importe quel ensemble dans lequel les variables, les fonctions, les prédicats du calcul représentent respectivement des éléments de l'ensemble, des fonctions de cet ensemble dans lui-même, et des parties de cet ensemble. Les prédicats représentent des qualités, s'ils sont à une place (unaires), ou des relations n -aires, entre n individus de cet ensemble. Ces notions seront précisées dans la suite de cet article. Le calcul des prédicats du premier ordre égalitaire adjoint au calcul des prédicats un symbole de relation, l'égalité, dont l'interprétation est obligée : c'est l'identité des éléments du modèle, et qui est axiomatisée en conséquence. Suivant le contexte, on peut parler simplement de calcul des prédicats pour le calcul des prédicats égalitaire. Le calcul des propositions est la partie du calcul des prédicats qui concerne ce qui ne contient pas les notions de variables, de fonctions et de prédicats et donc pas les quantificateurs ∀ et ∃. Il sert à formaliser essentiellement les déductions du calcul des prédicats. |
||||||||||||||||||||||||||||||||||||||||||||
Présentation alternée :↑ |
✔ |
- Si la surface d'empan présente le Nœud comme un non-nœud : c'est un non-nœud, qui est la présentation la plus pure des nombres d'enlacements. si la surface d'empan présente le Nœud comme un nœud, le Nœud contient alors du nœud, et le nœud sera révélé par la coupure nécessaire à la réorientation de sa surface. Il faudra calculer le nombre caractéristique de ce nouage et le nombre de nœud qu'il contient ! Np64 |
||||||||||||||||||||||||||||||||||||||||||||
Principe d'inertie ↑ |
✔ |
- Copernic, Kepler, Galilée, Newton, Einstein, |
||||||||||||||||||||||||||||||||||||||||||||
Principe de raison |
✔ |
- Leibniz, Heidegger, - Principe de raison, |
||||||||||||||||||||||||||||||||||||||||||||
Principe de réalité |
✔ |
-Principe de réalité, c’est quoi le principe de réalité, c’est le principe de la fuite, quelque chose existe dans le monde si je peux le fuir, si j’ai ma main qui brûle, c’est simple le principe de réalité, si j’ai ma main qui brûle j’ai intérêt à la changer de place, si la brulure continue à brûler, c’est qu’elle est à l’intérieur du système, elle a bien entamé le système, si la chaleur s’arrête c’est que le feu est dans la réalité, il est extérieur, c’est pas terrible, c’est un principe de fuite. -∃, il existe, |
||||||||||||||||||||||||||||||||||||||||||||
Prolétariat↑ |
✔ |
voir Discours du Maître et Discours du Kapital et de la Science. ( voir aussi à Religion !) | ||||||||||||||||||||||||||||||||||||||||||||
| Programme d'Erlangen | - voir Erlangen, ci-dessus, - Voir Klein Félix, |
|||||||||||||||||||||||||||||||||||||||||||||
Proposition↑ |
✔ |
- une proposition est une expression susceptible d'être Vraie ou Fausse. EU p 567 - résultats plus simple que des théorèmes, et donc qui ne méritent” pas de porter le nom de théorème, (L.PUJO-MENJOUET_Fonfamentaux,) |
||||||||||||||||||||||||||||||||||||||||||||
| Le calcul des propositions est la partie du calcul des prédicats (voir Prédicat et Calcul des prédicats) qui concerne ce qui ne contient pas les notions de variables, de fonctions et de prédicats et donc pas les quantificateurs ∀ et ∃. Il sert à formaliser essentiellement les déductions du calcul des prédicats. | ||||||||||||||||||||||||||||||||||||||||||||||
- Logiques antiques, gaogoa, en cours, - Algèbre de Boole, gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||||
Propre (noeud) ↑ |
✔ |
- Noeud composé d'un seul fil. Le plus petit noeud, hors le noeud trivial ( un cercle), est le noeud de trèfle. -Les nœuds propres et impropres se répartissent en deux familles dites Trèfles et Listing Np81 - Classification Noeuds et Chaines alternables, gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
| Propriété | ✔ | les propriétés se démontrent en général à la suite de la définition d’un objet ou d’une notion mathématique, dont on peut tirer directement, sans grande démonstration, des résultats. Ce ne sont des résultats plus simples que des propositions et donc des théorèmes.(?), (L.PUJO-MENJOUET_Fonfamentaux,) |
||||||||||||||||||||||||||||||||||||||||||||
Une proposition est un énoncé qui possède soit la valeur "fausse", soit la valeur "vrai". proposée par forum.mathforu.com |
||||||||||||||||||||||||||||||||||||||||||||||
Ψ |
✔ |
- voir fonction Ψ, JMV20150602, .pdf, | ||||||||||||||||||||||||||||||||||||||||||||
Psychanalyse↑ |
✔ |
- Traitement de cheval par la parole, la lecture et l'écriture, jusqu'au ...silence éloquent .. d'une écriture !. (pour l'analyse lacanienne !), buts.., essais !,
|
||||||||||||||||||||||||||||||||||||||||||||
Psychologie
Résilience |
✔ |
- les Lois de la pensée, c’est la Psychologie, la pensée au petite bonheur et à la chance, est-ce que ça a des Lois, c’est ce que les psychologues essaient de déterminer, tandis que lui Frege, il dit que la Logique, c’est les lois de la pensée nécessaire, ou de la pensée correcte, c’est le courant de l’Académisme, pourquoi, et même il ajoute et il ne s’en cache pas Frege, il pense que la Logique c’est une Science normative, et que les Sciences normatives ne disent pas comment les choses sont, mais elles disent comment les choses devraient être, les Sciences normatives c’est pas compliqué vous avez la Morale, la Logique et l’Esthétique, Alors que le projet de loi Climat et résilience est examiné à l’Assemblée nationale, le chercheur en sciences sociales Thierry Ribault se livre à une critique virulente de la « technologie du consentement » visant, selon lui, à rendre acceptable le désastre par tous. RIBAULT Thierry, Thierry Ribault vient de publier Contre la résilience. A Fukushima et ailleurs (L’Echappée, 368 pages, 22 euros).
|
||||||||||||||||||||||||||||||||||||||||||||
✔ |
- New psychose, |
|||||||||||||||||||||||||||||||||||||||||||||
Psychopathologie |
- la lecture c’est une tâche extrêmement difficile, très très troublante, à vouloir soigner les gens et à parler de psychopathologie, on oublie une chose c’est que c’est pas une pathologie que d’être confronté à un exercice qui nous constitue et qui est extrêmement difficile, il nous constitue et on le pratique malgré nous, JMV16062015 | |||||||||||||||||||||||||||||||||||||||||||||
Psychothérapie |
- Serpsy, - Psychothérapie institutionnelle, 1, 2, - Psychothérapie psychanalytique : Elle fait office d'entretien préliminaire, et est une porte pour l'analyse. R.Gentis pense qu'elle dépasse l'analyse .... pratiquée dans le cadre multipolaire qu'il définit , les 4 C ! (éducation populaire oblige !) : cure, cours (Théorie) , corps, cartel ! J-M.Vappereau rejette toute pratique qui ne soient pas dans la structure et sur la structure de la parole et du langage (les noeuds sont à la jonction de la parole et du langage (écrit et parlé).....). Nous pensons que ce sont des temps et des moments propres de l'élaboration du sujet et si le "scintillement" Signifiant est audible pour tous, de nombreux écrans en brouillent l'accès .... (notons la tension entre le scopique et l'auriculaire) |
|||||||||||||||||||||||||||||||||||||||||||||
Psychothérapie familiale |
- relève de l'Infirmerie, de l'Idéologie, de la Religion et du Ministère de l'intérieur. | |||||||||||||||||||||||||||||||||||||||||||||
Puissance
|
- Puissance d'un ensemble : C'est le nombre fini ou infini de ses éléments. - Synonyme de " nombre cardinal" |
|||||||||||||||||||||||||||||||||||||||||||||
Pulsion
Trieb Drive Déviation Déformation, |
✔ |
- de vie de mort ! 1920, -... les Triebs, l’érotisme qu’il soit anal, oral, scopique ou invoquant, j’évite d’employer le mot pulsion, parce que ça me fait penser à compulsion, Freud parle des quatre termes de la pulsion, mais il ne faut pas penser que c’est une compulsion, Lacan propose de le traduire par Drive, c’est déviation, toutes les fonctions sont déviées, modifiées c’est ce qu’on va voir avec les nœuds logiques, et cette déviation elle permet de dévier les fonctions organiques qui deviennent des lieux d’amour, liés à l’inconditionnel de la demande et tout ça à cause du désir et de la condition absolue du désir et qui est tout à fait différente de l’inconditionnel de l’amour, l’amour c’est plutôt capricieux, et ça ne marche jamais, alors que le désir c’est pire, c’est la tragédie, le désir, c’est quoi ?, c’est l’échec et la suppléance, on arrive à un peu de satisfaction dans l’échec, et c’est meilleur que toutes les satisfactions faciles, vous chercherez à retrouver dans l’amour qui est plutôt narcissique et qui va échouer aussi, car justement le problème se pose de comment composer les deux points de vue, intrinsèque et extrinsèque, JMV20150602, .htm, - le signifiant c’est crucial, pourquoi ?, parce qu’on commence par recevoir ça par les oreilles, la langue, le symbolique, ça rentre dans le corps par les oreilles dès les trauma, les parents parlent et ils ne s’entendent pas parler, ils ne s’occupent pas du fait qu’ils parlent et c’est ça qui intéresse les enfants, cette posture de la parole fonde la fonction phallique, et c’est le phallus symbolique voyez vous, c’est plus le phallus du mimétisme animal, et de la posture animale, qui va déterminer son territoire par des postures, des déjections, des cris, les parents parlent mais ils vont parler une langue, seulement voilà, dès le début, dès que ça rentre dans le corps, toute les fonctions organiques vont être transformées, c’est ce que Freud appelle Trieb, ce qu’on a malheureusement traduit par pulsion, comme si nous étions voués à des pulsions ou des compulsions, le Trieb freudien c’est la déformation, de n’importe quelle fonction organique, par le symbolique, par la langue, par le langage si vous voulez l’appeler comme ça, et moi je ne considère pas qu’il y a des langages, je considère qu’il a une différence cruciale entre la parole écrite, ça va diffracter le symbolique, et que cette diffraction elle se joue autour du continu et du discret, .. JMV16062015 , - antropie nég-antropie, - partielles : orale (la sphère) anale (le tore) génitale - scopique (cross-cap) invoquante (bouteille de Klein) - source objet but; - concept , mythe , entre psychique et somatique - pulsion de mort (constructive et destructive) |
||||||||||||||||||||||||||||||||||||||||||||
| Pur noeud | ✔ |
- Un pur noeud est un objet tel que la coupure passe par tous les croisements (Noeuds, p117) | ||||||||||||||||||||||||||||||||||||||||||||
| Q | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
q |
- variable pour la logique | |||||||||||||||||||||||||||||||||||||||||||||
quantification quantificateurs, quanteurs |
- - En mathématiques, les expressions « pour tout » (ou « quel que soit ») et « il existe », utilisées pour formuler des propositions mathématiques dans le calcul des prédicats, sont appelées des quantifications. Les symboles qui les représentent en langage formel sont appelés des quantificateurs (ou autrefois des quanteurs1,2). Les symboles : |
-W, | ||||||||||||||||||||||||||||||||||||||||||||
| QUINE | ✔ |
- Quine, - Quine a milité pour que l'on abandonne tout intérêt pour les autres logiques, non classiques, non standard. Quine est un logicien de la grammaire, il a bien formulé la différence qu'il y a entre les mathématiques et la logique, question que se posait Russell, dans les Principes de mathématiques , et Couturat; alors les mathématiques semblaient réductibles à la logique, courant logiciste, il ne faisait pas de différence entre les énoncés analytiques et les énoncés synthétiques de Kant,( question qui intéressait Frege), et que Cavaillès contredira dans les années 1930. Quine a trouvé le meilleur critère pour distinguer, marquer la césure entre la logique et les mathématiques, il dit que la logique c'est ce système de la coordination, plus ce que nous allons appeler le calcul des prédicats du premier ordre kantifiés , écrit avec un k, ces deux calculs forment la logique formelle , c'est le noyau de la logique, pour la science, et depuis les calculs de Boole et de Frege s'inscrivent là-dedans. JMV22062010-L130 -Quine en rejetant les logiques exotiques, et la logique modifiée empêche cet acte novateur qui est le plongement de la Logique classique dans la logique modifiée - Quine ne dispose pas du registre de l'écrit ni de cleui du discours qui n'ont pas besoin d'autres justifications divines, naturelles ou positives, lieux irréductibles quand les " mots font la chose" - « une logique, que tout le monde considère », même Quine la considère comme ça, en bon américain isolationniste, Quine dit : les logiques exotiques sont sans intérêt, la Logique Canonique Classique, au sens de Tarski, dit : « c’est celle qui est la plus simple et la plus élégante », JMV23062015 |
||||||||||||||||||||||||||||||||||||||||||||
| R | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
raison, raisonnement |
✔ |
- L'instance de la lettre dans l'inconscient ou la raison depuis Freud, ELP, 1957-05-09, (1950-1959) - voir pensée - tous ceux qui ont été des auteurs qui ont essayés de dégager une raison, sont des idéologues, ce sont des totalitarismes - Les formes de la pensée et du raisonnement, |
||||||||||||||||||||||||||||||||||||||||||||
Réalité |
✔ |
- voir Principe de réalité - ou Effectivité, le discours tenu, |
||||||||||||||||||||||||||||||||||||||||||||
| Référence | ✔ | Référence, 2017, Gregory Bochner, |
||||||||||||||||||||||||||||||||||||||||||||
refoulement↑
|
✔ |
- sa fixation : avoir lu quelque chose qui passe par les oreilles (les parents s'entendent pas crier !) - DenreFor, |
||||||||||||||||||||||||||||||||||||||||||||
regard |
✔ |
- le regard n'est pas la vision, le regard, c'est la lisibilité dans le regard, | ||||||||||||||||||||||||||||||||||||||||||||
relation d'équivalence ↑ |
✔ |
- Critère d'identité et de différence dans la classifications des différents plongements des noeuds dans la théorie classique (des noeuds). (N,p14). | ||||||||||||||||||||||||||||||||||||||||||||
relation↑
|
✔ |
- propriété qui porte sur l'ensemble des couples formés d'un élément d'un premier ensemble et d'un élément d'un second. Dedelicq560 - pour rendre compte de l'unité d'une entité complexe, il faut décrire son mode de structuration ; et cela revient à faire apparaître les relations qui unissent les constituants. Il y a une solidarité étroite entre structure et relation. voir article de J Ladrière dans EU |
||||||||||||||||||||||||||||||||||||||||||||
relation d'ordre ↑ |
✔ |
- - la théorie des ensembles ordonnés étudie en fait les structures d'ordre, c'est-à-dire les structures définies par une relation d'ordre. Or ce qui caractérise une relation comme relation d'ordre, ce sont certaines propriétés formelles (assymétrie, transitivité,) qui sont indépendantes des ensembles particuliers que la relation ordonne et de l'espèce particulière d'ordination dont il s'agit. Ces considérations peuvent se généraliser pour des structures plus compliquées. Ladrière 574 |
||||||||||||||||||||||||||||||||||||||||||||
| Relation d'ordre | ✔ |
- Une relation d’ordre dans un ensemble est une relation binaire dans cet ensemble qui permet de comparer ses éléments entre eux de manière cohérente. Un ensemble muni d’une relation d’ordre est un ensemble ordonné. On dit aussi que la relation définit sur cet ensemble une structure d'ordre ou tout simplement un ordre. | - W, |
|||||||||||||||||||||||||||||||||||||||||||
répétition↑ |
✔ |
- voir Le séminaire sur la Lettre volée de Lacan, à Lettre , sur l'automatisme de répétition, - la répétition freudienne, c'est la différence, et la différence produit l'identité, qui n'est pas la ressemblance. L'identité est donc le produit de la répétition freudienne qui produit la différence. C'est le même et ce n'est pas pareil, c'est le même entre l'écrit et la parole mais c'est pas pareil ! En terme de noeud, le même noeud peut avoir des présentations différentes..! La différence dans le même conduit à l'identité, ça implique un changement de logique. - répétition et hâte sont articulés dans le Temps logique, et sont complétés par la Sublimation qui égalise les sommets du graphe de Klein, articulés dans le fantasme (voir fantasme) - répétititon freudienne,012013, Voir le site TEE, - Psychanalyse et mathématique, Freud contemporain de Cantor, JMV, 2007 - voir Séminaire de JMV sur TEE année 2010 , |
||||||||||||||||||||||||||||||||||||||||||||
répétition (grande) |
✔ |
- la grande répétition, la répétition feudienne, du même et du différent de lui-même, le supposé savoir dont nous faisons sujet qui est en acte au principe du transfert. " ça claque " p 48 (Texte complet) - la répétition freudienne : le Trieb freudien c’est la déformation, de n’importe quelle fonction organique, par le symbolique, par la langue, par le langage si vous voulez l’appeler comme ça, et moi je ne considère pas qu’il y a des langages, je considère qu’il a une différence cruciale entre la parole écrite, ça va diffracter le symbolique, et que cette diffraction elle se joue autour du continu et du discret, alors comment parler à partir de là du Trieb ?, vous voyez que quand le symbolique tombe dans le corps, sur le corps, traverse le corps, il y a une très belle phrase de Lacan dans le direction de la cure où il dit que c’est jamais simple, que le névrosé est pas mal placé dans l’être, parce qu’il se plaint de ce passage, le névrosé se plaint parce que pour lui c’est une peine, donc il n’est pas question de dire qu’il faut se satisfaire de cette peine, mais le fait est que c’est effectivement une peine pour le sujet de se trouver être l’agent qui fait entrer le symbolique dans le monde et c’est ensuite par ses actions et y compris par l’écriture qu’il va modifier le monde, qu’il va transformer le monde, nous sommes des sujets ségrégatifs parce que le signifiant a cette structure qui est celle déjà avec la parole et ensuite avec l’écriture, le signifiant et la lettre ont toujours cette dimension de quelque chose qui se dédouble, 51.40, ça s’appelle la répétition freudienne, c’est ce que Freud va rencontrer dans les années 1920, c’est ce que Lacan appelle dans les Séminaires des années 1960, la grande différence, c’est cette pulsation qu’il y a à l’intérieur du symbolique, qui fait que c’est quelque chose qui n’a rien à voir avec la Nature, et même si ça va nous permettre d’inventer les machines , nous sommes la seule espèce animale qui inventons des machines, et même des machines électroniques, on a commencé par des machines à vapeur, on a même commencé par des outils, mais n’empêche que ça va nous permettre de construire des nouvelles machines, et c’est le fonctionnement de ce dédoublement et de cette identité, de cette pulsation qui fonctionne aussi dans nos machines mais qui fonctionne d’une manière spéciale dans le symbolique, c’est là qu’il faut distinguer le symbolique de l’ordre mécanique ou électronique, dans la mesure ou vous voyez bien que la machine peut reproduire des choses que vous lui apprenez à faire, mais elle ne va pas inventer ce que vous vous pouvez inventer si vous vous racontez des histoires, ou bien aussi des mathématiques, JMV16062015 |
||||||||||||||||||||||||||||||||||||||||||||
répétition (petite) |
✔ |
- Tore, - répétition freudienne, |
||||||||||||||||||||||||||||||||||||||||||||
représentation↑ |
✔ |
- représentation, - a-représentation |
||||||||||||||||||||||||||||||||||||||||||||
✔ |
- la résilience, concept anti freudien, anti lacanien. C'est un concept pour faire avaler toutes les couleuvres et les pires saloperies. Soit tu en meurs soit tu survis et donc ... tu es prêt pour affronter pire voir tu feras des merveilles! C'est un certain Cirulnik qui propage ce genre d'inepties ! C'est assez simple ! Struggle for life darwinienne ! Concept qui ravale le désir et le traite de façon éthologique, animale, c'est une conception névrotique ! Avec le père Orang outang ! C'est la sexualité reprodutrice du pouvoir, et non le sexe ! Inspiré de JMV .. , "piqué à", Lacan dans sa dernière leçon de séminaire à Paris, va nous expliquer que la Droite infinie, la D.I, le trauma, c’est une dieu, dei, qui est proche du Latin, mais qui est aussi féminisé, La dei, et il dit que ça c’est le fait du malentendu des parents, les enfants sont traumatisés, sauf les autistes qui eux ne rentrent pas dans ce traumatisme, et ils se protègent et certains vont présenter un retard organique de plusieurs mois à quelques années, donc la parole…. !, il y a cet espèce d’escroc, Cyrulnick, qui a écrit : la parole comme molécule, c’est publié en livre de poche, je dis un escroc, parce que là ça n’a pas pris, alors ensuite il a fait la Résilience, c’est un mec qui veut détruire la psychanalyse, la résilience, les animaux qui parlent, c’est la Nature, or la psychanalyse elle s’occupe de cette nécessité pour le corps, pour le sujet débile et prématuré que nous sommes, de recourir au Symbolique, pour ne pas dire le langage, parce que c’est plus compliqué, et qu’ensuite on a tendance à parler Des langages. C’est le Symbolique, et dans le symbolique, il y a la parole, et du fait du symbolique, il y des peuples qui inventent une écriture et il y a quelque chose qui se produit entre les deux qui s’appelle la lecture, la lisibilité, et je que la lisibilité apparait avec le deuxième composant du narcissisme, JMV20150602 , & .html, voir Covid-19, voir NewArticles, 2, |
|||||||||||||||||||||||||||||||||||||||||||||
| rétroaction signifiante | ✔ | - - Par exemple : l'effet du dit a des effets rétroactifs sur la situation, sur la compréhension d'un fait initial, ( d'un dit, d'un acte, d'une Histoire..), qu'il remanie, réinterprête, révèle !, reformule, en levant le refoulement (proprement dit, ou primordial). - Un signifié sous le Signifiant, - Après-coup, - figure de ... |
↑ | |||||||||||||||||||||||||||||||||||||||||||
rêve
|
✔ |
- voir Inconscient, La voie royale ... - Voir Artémidore, in Hadrian Bibliothèque, |
||||||||||||||||||||||||||||||||||||||||||||
rond |
✔ |
- rond, ..et rond... | ||||||||||||||||||||||||||||||||||||||||||||
rotation↑ |
✔ |
- - Deux aspects géométriques du narcissisme, JMV 17 mai 2011, les rotations du cube (48 isométries) |
||||||||||||||||||||||||||||||||||||||||||||
| S | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
Saturation |
✔ |
- pour le noeud borroméen : quand on ajoute deux croisements au dernier couple de croisements qui n'a pas été augmenté (JMV1062014-07'58") | ||||||||||||||||||||||||||||||||||||||||||||
Savoir |
✔ |
-
, dans le texte qui s'appelle Psychanalyse et enseignement , qui était dans Scillicet IV, qui se trouve dans Autres écrits, il dit 42.20, je m'étonne que personne n'ai mis en question le fait que l'enseignement c'est pas la transmission du savoir , alors aujourd'hui encore vous avez les folles et les fous de la transmission, papa maman, c'est transmettre le Nom, tout le monde veut se baigner dans du sacré, du religieux, du scientifique, personne n'est sérieux comme Lacan a pu l'être, ou comme Freud ( JMV09092014, 42.20) - que la parole c'est continue et que ça dit la vérité, alors que l'écriture est discrète et produit du savoir, c'est à cette occasion là qu'on parle du savoir, qui n'est pas la connaissance, ce n'est pas non plus un savoir faire, c'est un savoir lire, savoir écrire, savoir compter, le savoir ça commence avec la différence entre l'écrit et la parole, JMV09092014, - le Savoir est toujours binaire, Lacan dit plutôt bipolaire, la bipolarité du savoir est que l’inconscient introduit dans cette bipolarité une dimension de la dispute, c’est ça qui va apparaître comme étant dissymétrique, c’est lisible si on arrive à voir comment la bipolarité va se déformer, c’est ça Trieb, Lacan propose de parler de trajet, de Drive en anglais, mais c’est la déformation , JMV26092014, 49..., |
||||||||||||||||||||||||||||||||||||||||||||
Savoir absolu |
✔ |
- - du savoir absolu chez Hegel |
||||||||||||||||||||||||||||||||||||||||||||
Schéma F |
✔ |
- Schéma F, Etoffe, p18,22, JMV, - Schéma F , Ecrits p53 - Schéma F, complet (old) ; Schéma F (new) provisoire; |
||||||||||||||||||||||||||||||||||||||||||||
Schéma I |
✔ |
- Schéma I , 2, Ecrits p371, La psychose, Psychose et personnalité, Psychose aujourd'hui, autour de Schreber, - de la psychose paranoïaque dans ses rapports avec la personnalité, Thèse de LACAN, psychanalyse.com, - l'appareil psychique, - Clinique du processus du neuds, JMV, 12-12-2014 |
||||||||||||||||||||||||||||||||||||||||||||
Schéma L |
✔ |
- Schéma L , Ecrits p53 - Schéma L sur le cross cap, JMV, Etoffe, p323, - Schéma L, SIBONI, - Lettre 52 au Schema L, & Registres - Schema L & Lettre 52, complet; -l'appareil psychique, - schéma L sur le plan projectif, 2, 3, - Clinique du processus du neuds, JMV, 12-12-2014 -cette difficulté majeure de la clinique analytique, qui fait que tous les escrocs se précipitent là-dessus, pour nous faire croire qu’ils sont cliniciens, vous allez voir, c’est juste après le schéma R, (p553 des Écrits de Lacan), vous vous souvenez dans les Écrits de Lacan le schéma R, vous savez moi, j’ai pris le schéma de Freud de la Lettre 52, et je l’ai plié et déplié, qu’est ce qu’il dit Lacan tout de suite après ce schéma R, on va conclure comme ça ce soir, il dit la chose suivant, il écrit la chose suivante p554 : Ce schéma permet en effet de démontrer les relations qui se rapportent non pas aux stades pré oedipiens qui ne sont pas prétendus inexistants, c’est ce que je vous ai dit : trauma et incorporation, mais analytiquement impensable (comme l’œuvre trébuchante mais guidée de Mélanie Klein le met suffisamment en évidence), guidée parce qu’elle est freudienne !, mais aux stades prégénitaux mais aux stades prégénitaux en tant qu’ils s’ordonnent dans la rétroaction de l’Œdipe. Se réordonner dans la rétroaction de l’Œdipe, c’est une escroquerie que de prétendre trouver la cause de la psychose en allant observer quoi que ce soit dans la cure, ça ne s’observe pas ! Ca se reconstruit logiquement rétroactivement à partir de l’Œdipe, les mecs qui voudraient soigner les psychotiques, ils peuvent aller se faire voir, parce que n’importe quelle analyse, c’est un traitement de la psychose, c’est pas seulement le traitement possible, c’est-à-dire celui qui pourrait ne pas avoir lieu, c’est le traitement contingent de la psychose, le traitement contingent de la psychose c’est la psychanalyse, c’est en analysant névrose et perversion, que le sujet est invité à reconquérir la lecture, et à construire justement un objet qui n’est pas un Savoir, qui n’est pas une Vérité, qui est comme l’objet transitionnel, il est pris dans l’éclatement de l’objet répulsif de la phobie et attractif de la perversion, dans l’éclatement du désir dans le corps, à partir du moment de l’incorporation, vous avez des enfants qui fabriquent cet objet, qui n’est pas une synthèse, mais qui est un objet bien construit, c’est un objet transitionnel, ça veut dire quoi, c’est un objet répulsif, répugnant même, et attractif en même temps, et faire rentrer ça à l’âge adulte, dans son existence, construire ce type d’objet, je vous dis c’est comme une boussole, ça vous permet d’apprendre à lire, donc une psychanalyse, c’est une pratique de cette tâche analysante qui consiste ensuite à être mordu par ça, et ensuite à faire ça toute sa vie. JMV20150602 |
||||||||||||||||||||||||||||||||||||||||||||
| Schéma R | ✔ |
- - Schéma R, Ecrits p553 -l'appareil psychique, - Clinique du processus du neuds, JMV, 12-12-2014 |
||||||||||||||||||||||||||||||||||||||||||||
Science |
✔ |
- La science veut perfectionner le monde, c'est une conséquence du Christianisme et de l'Euchariste, incarner le corps de Dieu, et le rendre perfectible ! - la science son objectif c'est de suturer le Sujet de la science, et que le théorème de Godel (incomplétude) montre que c'est impossible, donc le sujet de la science est anti-nomique avec la science, et que la science se définie de cette antinomie même avec son propre sujet. (JMV 02092014, II-01.09.50), 2, - les sciences normatives sont : La Logique, l'Esthétique et la Morale . - Science sur gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
Section transverse |
✔ |
- ou "coupure" transverse Noeud 287, préférer Section à coupure, la coupure étant plus étendue, globale, que la section qui est locale. - mise en continuité dans une chaine de deux ou trois brins de ficelles, (consistances), de ronds différents. ou d'un même rond. |
||||||||||||||||||||||||||||||||||||||||||||
Seifert |
✔ |
- voir surface de Seifert | ||||||||||||||||||||||||||||||||||||||||||||
| Sémantique de KRIPKE | ✔ |
En logique mathématique, la sémantique de Kripke est une sémantique formelle utilisée pour les logiques non-classiques comme la logique intuitionniste et certaines logiques modales. Elle a été développée à la fin des années 1950 et début des années 1960 par Saul Kripke et est fondée sur la théorie des mondes possibles. | ||||||||||||||||||||||||||||||||||||||||||||
Séparation |
✔ |
- Deuxième opération fondamentale, la séparation après l'aliénation, où il convient de formuler la causation du sujet dans un procès qui voit le le vel faire retour en velle (Ep843) , -"Venons à la seconde opération, où se ferme la causation du sujet, pour y éprouver la structure du bord dans sa fonction de limite, mais aussi dans la torsion qui motive l’empiétement de l’inconscient. Cette opération nous l’appellerons : séparation. Nous y reconnaîtrons ce que Freud appelle Ichspaltung ou refente du sujet, et saisirons pourquoi, dans le texte où Freud l’introduit, il la fonde dans une refente non du sujet, mais de l’objet (phallique nommément). |
||||||||||||||||||||||||||||||||||||||||||||
Série
|
✔ |
- Une série est convergente si la suite de ses sommes partielles est convergente. Cauchy expose dans ses cours de l'Ecole polythechnique, son célèbre critère de convergence pour les suites numériques. - Série des fonctions, - Série géométrique, et suite..., |
||||||||||||||||||||||||||||||||||||||||||||
Sexe
|
✔ |
- Le corps écrit, déviant ses organes pour faire des lettres, il est entré dans cette fonction par les oreilles, aussi, "ça parle" ! Il n'y a pas de déviation sexuelle car le langage, le sexe, maintenant, de ce mammifère prématuré n'est que déviation, in " ça claque ", p60, JMV - Le sexe "fou", relève de la Nature ?!, de la division cellulaire, de la répétition, de l'éthologie, voir de la Sexologie (dompter la nature par la ruse !). - la sexualité, plutôt sexe que sexualité, Foucault dit que la sexualité c’est historique, Sexe, c’est inanalysable, c’est inexplicable, c’est ininterprétable, c’est insensé, on peut vouloir vous faire croire ; parce qu’il faut que les petits soldats se reproduisent, alors c’est fait pour se reproduire, pour faire des enfants, c’est une analogie, Sexe, c’est le lieu de la condensation par excellence, du trauma jusqu’à la castration, ça nous coupe la chique, c’est ce que je trouve formidable, moi je ne comprends pas ces psychanalystes qui disent avoir un savoir sur la jouissance, et qui disent que c’est pas bien ou que c’est bien, le désir c’est quelque chose de formidable, ....le désir c’est le truc impossible et ça emmerde tout le monde, mais c’est ce qu’il y a de plus extraordinaire, si sexe ça a un intérêt, c’est que c’est insensé ! JMV11092007; Le noeud borroéen généralisé, - La parole et le sexe, c'est tordu, alors on doit aujourd'hui s'en débarasser ! On cultive le Moi, l'apparence, plutôt que la parole du sujet ! |
||||||||||||||||||||||||||||||||||||||||||||
Sexualité ↑
|
✔ |
- relève de la gymnastique, et des Noms du père, ( voir M.Mauss) - La sexualité depuis Freud est la réalisation en acte de la structure du sujet , le fonctionnement même de l'appareil psychique. Vappereau LU, 4=3 p 75 - faire un tour dans l'autre au risque du désir, en affrontant les lois freudiennes - figures : métaphores, métonymie... - la sexualité humaine est perverse et polymorphe, elle n'échappe pas aux fétiches ! dans le fantasme. - l'exercice de la sexualité ou le non exercice de la sexualité génère de la culpabilité... - le mésusage de la sexualité crée de la culpabilité . Mars 2003 PG - L'amour du tout, partie 3, 1992, JMV sexualité freudienne |
||||||||||||||||||||||||||||||||||||||||||||
| Sexuation | ✔ |
- la sexuation relève , des signifiants, du discours, des identifications, - La sexuation, pour Lacan, est définie par le tryptique Hétéro, Hystérique, Paranoïaque ! Hétéro = aimer une femme, Hystérique = ne pas se prendre pour une femme et Paranoïaque = vouloir être une femme ! - Tableau des Identification sexuées, - Lecture des formules de la sexuation, texte ingéral, JMV 2007 (SEPARATION), voir 6 annexes de logique, ici la Table des matières, Lecture des formules kantique de la sexuation 2009 et 2012, JMV, - les formules de la sexuations, où ? - Sexuation, |
||||||||||||||||||||||||||||||||||||||||||||
| Schéma | ✔ | - Schémas, SIBONI, - Le schéma est un diagramme (du grec ancien σχῆμα / skhễma (« manière d'être », « forme », « figure », « extérieur », « apparence », « faux-semblant »)) est une représentation simplifiée servant de vecteur de communication et souvent codifié ou symbolisé. Le mot prend généralement le sens de graphe selon le domaine dont on parle :
|
||||||||||||||||||||||||||||||||||||||||||||
Signe
|
✔ |
- signifiant/signifié, Saussure - fait signe de quelque chose à quelqu'un - Boudhisme; - à propos du Signe, vital et non humain, JMV20110201_01, page 11, 350 |
||||||||||||||||||||||||||||||||||||||||||||
Signifiant↑ |
✔ |
- Le signifiant est articulé ! (Essaim p 42), son étude se produit de l'ensemble articulé de différents éléments au lieu d'un seul ! - la doctrine du signifiant est associée à la logique étirable qui est la topologie du sujet. Il s'agit d'une topologie qui s'obtient à partir de la logique de Boole par adjonction d'un opérateur d'intérieur.(voir Groupe). Essaim p 36. - Le signifiant S 1 , «le Un » incarné de la langue, (Hen !), reste indécis entre les étages séparés de la structure, ( en dessus, lieu des Lettres capitales, des Nombres, des nœuds générateurs , ou en dessous de la barre ou courent les petites lettres) comme pour le nœud ce qui fait tenir ensemble les ronds ! Ce graphe s'homologue bien à la donnée d'une chaîne ou d'un nœud. De la même manière que le parcours de la Lettre déterminait le graphe, dans ce nouvel aspect la Chaîne ou le Nœud impose la structure de groupe. La distinction entre les deux présentations graphe ou chaîne réside dans la différence des structures formelles obtenues : les mots qui constituent un langage artificiel ne forment pas un groupe algébrique. |
||||||||||||||||||||||||||||||||||||||||||||
| Singleton | ✔ |
- en mathématique et en théorie des ensembles, un ensemble E, est un singleton lorsqu'il ne contient qu'un seul élément, a, il s'écrit alors E = {a} (source wiki) | ||||||||||||||||||||||||||||||||||||||||||||
Sinthome↑
|
✔ |
- Joyce le symptôme et non le Sinthome, Joyce est hystérique et non psychotique !. C'est La psychanalyse freudienne qui est un Sinthome dans la production des nouvelles modalités du Symptôme, ancien discours qui survit dans un nouveau discours... dans une nouvelle clinique.... - Il s'agit d'un quatrième rond, le sinthome (écriture ancienne en lettres latines) constituant du symptôme (écriture nouvelle injetctée de grec) actuel de la psychnalyse, en tant que un symptôme est constitué, selon Marx, par le survivance d'un ancien système de production dans le nouveau. (in Des chaines, des noeuds et ronds. Argument cours TEE sept 2014) -- Clinique du processus du neuds, JMV, 12-12-2014 |
||||||||||||||||||||||||||||||||||||||||||||
Soury↑
|
✔ |
- 6433-6433, .swf, .pdf, noeud de Soury, - Noeud de Soury, voir Noeud de Soury - Chaines et noeuds 3 Tomes, Edités par M.Thomé et CH.Léger - Voir " ça claque " , JMV, revue Essaim |
||||||||||||||||||||||||||||||||||||||||||||
Spéculaire↑ |
- image dans le miroir | |||||||||||||||||||||||||||||||||||||||||||||
Stade du miroir ↑ |
- Seul le Stade du miroir est Universel pour Lacan. - Le Stade du miroir comme formateur de la fonction du Je telle qu'elle nous est révélée dans l'expérience psychanalytique 17 juillet 1949, Ecrits p93, Lacan, - Remarque sur le rapport de Daniel Lagache : " Psychanalyse et structure de la personnalité", 1960, Ecrits p647, Lacan - |
|||||||||||||||||||||||||||||||||||||||||||||
Structure↑ |
✔ |
- Le désintérêt à l'égard de la structure est lié à des fonctions ritualisées dans la pratique des orifices du corps. Il en est ainsi dans l'Homosexualité greco-arabe, et dans la pratique de l'Eucharistie (voir ce terme). Dans la psychanalyse "orhodoxe", la perennité de l'Institution est confiée aux filles (fonction épiclère), transmission à connotation incestueuse ...) et à la pratique étendue .. de l'analyse infinie ou temponnée sur un symptôme compatible, ou à une identification à l'analyste et relais olympique du flambeau dans le consensus du groupe ! ( voir AME..) - Les Eléments de mathématique de N.Bourbaki prennent le concept de structure comme concept fondamental : ils présentent les mathématiques comme le science des structures. Ainsi la théorie des ensembles ordonnés étudie en fait les structures d'ordre, c'est-à-dire les structures définies par une relation d'ordre. Or ce qui caractérise une relation comme relation d'ordre, ce sont certaines propriétés formelles (assymétrie, transitivité,) qui sont indépendantes des ensembles particuliers que la relation ordonne et de l'espèce particulière d'ordination dont il s'agit. Ces considérations peuvent se généraliser pour des structures plus compliquées. L'une des conditions essentielles dans la définition d'une structure, c'est le caractère transposable de la relation qui la spécifie (Bourbaki, Elements de mathématique Chap IV, par 1,3,4). Intuitivement on peut exprimer cette condition en disant que cette relation doit être indépendante de son support qui est de nature ensembliste, or ce par quoi elle a ce caractère c'est son aspect formel. Ladrière 574 - en logique, chaque assignation aux variables de valeur de vérité sera appelé structure. Ici, la démarche se rapproche de cet usage logique du mot structure. Essaim p 36 |
||||||||||||||||||||||||||||||||||||||||||||
Structure |
✔ | La signature d'une structure comporte un ensemble de symboles de fonctions et de symboles de relations avec une fonction qui associe à chaque symbole s un entier naturel n = ar ( s ) qui est appelé l'arité de s, puisqu'il est l'arité de l'interprétation de s (voir ci-dessous : L'interprétation). La plupart du temps, l'égalité fait partie du langage par défaut, et n'apparaît pas dans la signature. L'interprétation de l'égalité est toujours l'identité, quelle que soit la structure. Les signatures en algèbre ne contiennent souvent que des symboles de fonctions. En algèbre universelle une signature ne contenant pas de symboles de relation est appelé une signature algébrique, et une structure ayant une telle signature est appelée algèbre. |
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
| Structure mathématiques, | ||||||||||||||||||||||||||||||||||||||||||||||
En mathématiques, une structure désigne toute théorie « plus forte » que la théorie des ensembles, c'est-à-dire une théorie qui en contient tous les axiomes, signes et règles. C'est donc une théorie « fondée » sur la théorie des ensembles, mais contenant également des contraintes supplémentaires, qui lui sont propres, et qui permettent également de définir de nouvelles structures qu'elle inclut. Cette notion est ainsi une puissante contribution à l'hypothèse selon laquelle la théorie des ensembles fournit le fondement des mathématiques. |
W, |
|||||||||||||||||||||||||||||||||||||||||||||
une liste non exhaustive de structures :
|
↑ | |||||||||||||||||||||||||||||||||||||||||||||
| ✔ | Structure en logique mathématique, | |||||||||||||||||||||||||||||||||||||||||||||
En logique mathématique, plus précisément en théorie des modèles, une structure est un ensemble muni de fonctions et de relations définies sur cet ensemble. Les structures usuelles de l'algèbre sont des structures en ce sens. On utilise également le mot modèle comme synonyme de structure (voir Note sur l'utilisation du mot modèle). La sémantique de la logique du premier ordre se définit dans une structure. |
W, |
|||||||||||||||||||||||||||||||||||||||||||||
Structure algébrique ↑ |
✔ |
- Une structure algébrique consiste en principes de calculs. L'algèbre est la science du calcul avant de devenir science littérale. Elle comporte les notions de contraintes et de réduction. Ses structures sont spécifiées par des propriétés, rendues par des axiomes (schémas vides à remplir à chaque fois) Les structures algébriques sont toujours définies pour un type d'objet précis : un domaine ou une loi de composition. Ensuite elles le sont par des axiomes. Donc les axiomes varient avec les structures. Leurs propriétés sont attachées à des modes de compostion d'éléments. Il faut définir le domaine où s'effectuent les combinaisons et les moyens d'obtenir le résultat de la compositions, ce sont les lois des mathématiciens. La loi de composition et son domaine d'effectuation propre s'appelait auparavant une opération (la somme, le produit, dans le domaine numérique, mais la soustraction et le quotient vont se trouver traité différemment). Essaim p 36. - il existe une corrélation entre une structure algébrique et un mode de calcul dans un domaine numérique puis littéral. -le calcul dépend toujours d'une structure algébrique; Essaim p 37 - Il existe une difficulté à concevoir ces calculs de manière purement littérale. Le passage de l'arithmétique à l'algèbre doit aider à acquérir une intuition algébrique utile dans le l'exploration de ce bien peu d'intuition géométrique qu'il y a autour du noeud ! Essaim p 41 |
||||||||||||||||||||||||||||||||||||||||||||
Structures Freudo Lacanienne du Symptôme, SFLS ↑ |
✔ |
- Table, - Pernépsy, - La clinique d'avant la psychanalyse, - Nouvelle psychose, - Psychose, ordre du discours, - deux présentations topologiques de la psychose, y manquent une troisième : les 3 ronds libres, non noués... - |
||||||||||||||||||||||||||||||||||||||||||||
Structure du langage ↑ |
✔ |
- La structure du langage, c'est le principe d'inertie (voir cet item), (Encore p100), pour savoir ce qu'est le principe d'inertie : faire un exercice de mathématique ! ça différencie la parole de l'écrit ! Le principe d'inertie aboutit à la gravitation, c'est-à-dire au principe d'influence, soit la formule du premier fantasme scientifique écrite ! Le fantasme est une formule écrite dont les symptômes sont les déclinaisons. L'objet masqué et absent qui tord la trajectoire du langage est l'objet a. - le phonème, il se réalise en Signifiant, dans le son et en lettre dans le graphisme, et l’économie du graphisme, et l’économie du son, l’économie du signifiant, Lacan dit l’inertie, c’est le principe d’inertie = la structure du langage, l’inertie n’est pas la même - = lisibilité = refente ou division = castration - La lettre, la fonction littorale de la lettre - l'amour du tout, partie 3, 1992, JMV |
||||||||||||||||||||||||||||||||||||||||||||
Structure et linguistique |
✔ |
- - linguistique et psychanalyse, - Le langage, (la langue), est la condition de l'Inconscient, in Langage, gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
Structure de groupe ↑ |
✔ |
- Ensemble d'éléments muni d'une loi de composition interne associative admettant un élément neutre et pour chaque élément de l'ensemble, un élément symétrique. - On appelle groupe tout ensemble (G, *) muni d'une loi de composition interne vérifiant les trois propriétés suivantes:
Aussi: un groupe est un monoïde inversible. Conséquence: élément neutre unique; chaque élément admet un inverse unique; tous les éléments sont réguliers pour la loi *. - Les groupes, Jean DIEUDONNE, |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Structure du sujet |
- Topologie du sujet, [Signifiants- Nombres, Lettres, Noeuds, Dire / / projection-ruissellement/Schématisme et ravinement/ recomposition et ravissement / retour aux Signifiants...] T , - voir Sujet, |
|||||||||||||||||||||||||||||||||||||||||||||
| Structure logique du sujet divisé, | - Structure logique du sujet divisé, source cours de JMV du mardi 15 juin 2010, Construction du poinçon et des schémas, | |||||||||||||||||||||||||||||||||||||||||||||
Style |
✔ |
- Lacan le dit dans le complément de sa thèse, Schizographie, il dit que les grands écrivains donnent les grands styles littéraires, et les grands styles littéraires sont liés à la paranoïa, il parle de Rousseau, le méchant Rousseau qui avait abandonné ses enfants, il a eu un succès littéraire énorme. | ||||||||||||||||||||||||||||||||||||||||||||
Subjectivité scientifique |
✔ |
- la subjectivité scientifique, Lacan la définit de trois termes : il dit c’est a subjectivité du savant, que le savant partage avec l’homme de la civilisation qui soutient cette science. | ||||||||||||||||||||||||||||||||||||||||||||
Subordination |
- Il y a deux relations dans les propositions, la subordination et la coordination, et Grevisse il dit coordination parce que dans un traité de logique, la coordination est traitée en logique, alors que la subordination elle est traitée en grammaire, cela montre qu’il y a une proximité entre la logique et la grammaire, vous voyez que la logique au niveau de la coordination, c’est de la grammaire, mais les grammairiens abandonnent ça aux logiciens parce que, il y a une histoire de vérité qui va apparaître, un calcul sur le Vrai et le Faux. - la coordination c’est quoi, c’est l’étude des connecteurs de coordination, vous avez ça dans le Grevisse, dans les Grammaires du français, qu’est ce qu’on peut faire avec des propositions, dans la langue, soit il y a la subordination, la principale et la subordonnée, soit il y a la coordination par des connecteurs, V01-47.00 ; qui sont appelés des conjonctions de coordination, et Grevisse il renvoie la coordination aux logiciens, il dit maintenant si vous voulez étudier la coordination des propositions dans la langue, il faut faire de la logique, par contre la grammaire elle traite de la subordination, JMV20150602, .pdf, |
|||||||||||||||||||||||||||||||||||||||||||||
Suite
|
✔ |
- N désignant l'ensemble des entiers naturels, une suite d'éléments d'un ensemble E est une application de N , ( ou une partie de N de la forme [n,+ ∞[ ), vers E. - Une suite est dite convergente si la variable qu'elle représente admet une limite finie lorsque n tend vers l'infini. - Toute suite convergente et une suite de Cauchy, (Melh) - e désignant un nombre arbitrairement petit et positif, on appelle suite de Cauchy , appellation due à son contemporain Bolzano , une suite numérique (u n ) pour laquelle |u m - u p | < e à partir d'un certain rang. Plus précisément, en notations "modernes" (depuis Weierstrass et Bourbaki ) : ...voir Suites de Cauchy, - Suites divergentes : Une suite non convergente est dite divergente . On dit aussi qu'elle diverge . Ce qui ne signifie pas que u n tend vers l'infini. - Une suite est dite numérique si ses éléments un; sont des nombres réels (ou complexes, mais alors on préfère parler de suite complexe ). L'exemple 1 est une suite numérique (de nombres rationnels). Une suite à valeurs dans N est parfois qualifiée de suite entière . - Suite de Fibonacci, ci-dessous, |
||||||||||||||||||||||||||||||||||||||||||||
Suite de Fibonacci |
✔ |
- voir Fibonacci , - R suites, F suites, suite des rapports..; |
||||||||||||||||||||||||||||||||||||||||||||
Sujet
|
✔ |
- le sujet de la psychanalyse, c'est le sujet de la science, Ecrits p 858, 863, - Sujet , in J.SIBONI, Lutecium, les Mathèmes de Lacan, - Généalogie du sujet, de Saint Anselme à Malebranche, Vrin, 2007, BOULNOIS.Olivier, Ed., préface de , in Langage-Bibliographie, gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
| Surface | ✔ |
-les sufaces topologiques sont des objets topologiques de dimension deux. Les surfaces sont ces objets découpés par des lignes, la structure de la surface est définie par des coupures de dimension Un. Les noeuds, sont ces coupures dans les surfaces, ils indiquent la structure de la surface. La structure de la surface c'est la coupure, son lieu en est l'étoffe ! Etoffe p 15 - la surface de l'étoffe (ou quotient du groupe fondamental –Essaim, chap I, p 60), est identifiée à la libido, (E a 30, p846). -Théorie des surfaces sans bord. -Théorie des surfaces à bord présentant un seul cercle composant (troué une seule fois) -Bord : le bord d'une surface topologique est la réunion des segments des morceaux d'étoffe qui n'on par servi au montage par couture. Le bord de la surface (une cercle) est un composé, une réunion de cercles distincts ou composants de bord, et ces composants du bord forment le Nombre de bord. Un trou comme rupture de surface est défini par un cercle composant du bord d'une surface topologique. Le trou imaginable intuitif peut alors être réduit à un invariant bien construit, le composant de bord. Il n'y a pas de trou imaginable dans la suface intrinsèque, seul son bord y insiste, et le trou existe pour nous. Ceci pour un type de trou parmi les trous …. Etoffe p79 -A toute surface topologique avec ou sans bord correspond une surface sans bord. |
||||||||||||||||||||||||||||||||||||||||||||
Surface d'empan ↑ |
✔ |
- C'est la surface d'engendrement du noeud. |
||||||||||||||||||||||||||||||||||||||||||||
Surface de Seifert ↑ |
✔ |
- empilement de cercles de Seiferts aux cycles orientés admettant un noeud comme bord ! Np30-31, - surface de Seifert, - Surface d'empan et surface de Seifert : la surface d'empan (orientable) est une généralisation de la surface de Seifert. - Le DI, la droite infinie, 2006, J-M.V |
||||||||||||||||||||||||||||||||||||||||||||
Surface topologique intrinsèques ↑ |
✔ |
- Sphère, tore, plan projectif, bouteille de Klein, - Les surfaces remarquables, - Le DI, la droite infinie, 2006, J-M.V - Etoffe, JMV, 1988 |
||||||||||||||||||||||||||||||||||||||||||||
Surmoi ↑
|
✔ |
- pseudo instance - voir seconde topique chez Freud - Héritier du complexe d'Oedipe selon Freud. - divers textes ... |
||||||||||||||||||||||||||||||||||||||||||||
Surréalisme
|
✔ |
- Il en va du surréalisme comme du classicisme, du romantisme, ou du baroque dans une moindre mesure : ce terme couvre au moins trois espaces de langue et de pensée, qui vont de l'histoire des formes ou des idées (un groupe actif dans la période 1924-1969) à la caractérisation transhistorique (une tendance présente depuis la « bête de Lascaux », pour reprendre le titre de l'ouvrage de Maurice Blanchot, jusqu'au slogan publicitaire contemporain, en passant par Piranèse ou Bosch), et sans qu'on puisse tenir pour rien sa banalisation dans une langue commune, venant désigner tout ce qui est absurde, surprenant ou simplement curieux.
On pourrait estimer que ces trois états du mot marquent l'achèvement du projet même des premiers surréalistes, en faisant passer la subversion littéraire ou picturale, la révolution des mots et des images dans l'espace de la vie et de l'activité humaines envisagées selon leur dimension anthropologique la plus large. Et l'on se gardera, après eux, de négliger l'influence en retour du quotidien, du trivial et du journalistique sur l'inconscient à l'œuvre dans les rêves, l'amour, l'humour et l'imagination. Marx et Freud rejoignent ici Rimbaud pour exiger un changement de vie, non d'esthétique ou de pensée. Ainsi le surréalisme fut-il avant toute forme écrite ou peinte une « pure pratique d'existence », comme le soulignait Maurice Blanchot, « pratique d'ensemble portant son propre savoir, une théorie pratique ». L'histoire d'une notion n'est pas seulement celle de ses inventeurs, et le surréalisme naît d'une conjonction complexe d'héritages (Lautréamont, Nerval, Jarry, Lewis Carroll), et de revendications (Sade). À cette conjonction inaugurale prennent part Apollinaire, premier utilisateur reconnu du terme, associé dans ce cas à une transposition poétique du réel, et l'influence notable de Pierre Reverdy. Un groupe d'abord informel est issu de la revue d'inspiration dadaïste Littérature (1919-1924), autour d'André Breton, [...] - Centre d'études, Pompidou, l'âne pourri, |
||||||||||||||||||||||||||||||||||||||||||||
Syllogisme ↑ |
✔ |
- Le syllogisme, - voir S1T1 et (S1T1)mon. - Boole veut faire entrer la syllogistique d'Aristote dans S1T1, soit le calcul des prédicats quantifiés. - syllogisme, Barbara et consoeurs, propositions, carré logique, - Syllogisme Wiki, - |
||||||||||||||||||||||||||||||||||||||||||||
Symboles |
✔ |
- Histoire des symboles, - Symboles mathématiques courants, - Symboles mathématiques et codes ..texte, numérique, html, (out) |
||||||||||||||||||||||||||||||||||||||||||||
| Symbolique La | ✔ | - Imaginaire, - La symbolique est un ensemble de symboles propre à un domaine, un système de signes particulier. Elle peut concerner, du côté des objets désignés, un être naturel (ex. : la symbolique du lion), un art ou une technique (ex. la symbolique architecturale), une religion (la symbolique chrétienne), etc. ou, du côté de ceux qui désignent, un peuple (la symbolique viking), un groupe humain (ex. : la symbolique des alchimistes), une école (la symbolique des romantiques), une époque (la symbolique médiévale), etc. Les symboles ont tendance à s'organiser en constellations, ils ne sont pas isolés, ils forment des réseaux ; par exemple, la symbolique de la naissance concerne des vivants, des moments, des personnes, des pensées, etc. reliés de façon significative. Chaque culture a une symbolique. Pour Lévi-Strauss, « toute culture peut être considérée comme un ensemble de systèmes symboliques au premier rang desquels se placent le langage, les règles matrimoniales, les rapports économiques, l'art, la science, la religion. Tous ces systèmes visent à exprimer certains aspects de la réalité physique et de la réalité sociale, et plus encore, les relations que ces deux types de réalité entretiennent entre eux et que les systèmes symboliques eux-mêmes entretiennent les uns avec les autres ». Pierre Bourdieu a développé cette analyse des systèmes symboliques en en montrant le pouvoir et la violence. Les symboles de propitiation de toutes les religions, d'intercession devenue ciment culturel, se groupent en systèmes essentiellement religieux quelquefois politiques, qui forment un langage cohérent : mythe, rituel, rêve, récit initiatique, poème, tableau, etc. Les symboles naturels, de la Nature sans artefact de l'homme, tout autant, sont perçus comme des systèmes non chaotiques : les « Quatre Éléments » s'appellent les uns les autres, les parties d'un arbre (racines, tronc, branches ; feuilles, fleurs, fruits) entrent en relations organisées, etc. Les couleurs constituent un monde. Les symboles forment donc des systèmes, à savoir des complexités variées, interactives, organisées, totales et finalisées.
|
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
| - voir Les structures anthropologiques de l'imaginaire, Gilbert DURAND, Dunod, 1969, | ||||||||||||||||||||||||||||||||||||||||||||||
Symbolique Le ↑ |
✔ |
- Le symbolique ce n'est absolument pas naturel, c'est artificiel, mais ça nous constitue, et nous sommes surpris de ce que la langue nous fait faire. - voir ci-dessous Symptôme, |
||||||||||||||||||||||||||||||||||||||||||||
Symétrie ↑ |
✔ |
- Symétrie et groupe, - Afin de préciser le narcissisme, JMV, 2007, Intrinsèque extrinsèque, la géométrie, la symétrie, la symétrie miroir, L'envers du narcissisme, |
||||||||||||||||||||||||||||||||||||||||||||
Symétrie miroir ↑ |
✔ |
- - Afin de préciser le narcissisme, JMV, 2007, Intrinsèque extrinsèque, la géométrie, la symétrie, la symétrie miroir, L'envers du narcissisme, - Deux aspects géométriques du narcissisme, JMV 17 mai 2011 |
||||||||||||||||||||||||||||||||||||||||||||
Symptôme ↑ |
✔ |
- Les symptômes sont femmes, quelque soit le sexe du sujet ! donc tout ça ensuite mérite d’être élaboré, construit, poursuivi, mais ça n’intéresse pas les psychologues, les médecins, et du coup ça n’intéresse pas les analysants, c’est bien dommage, parce que du coup ça fait que le discours il est complètement dégradé, parce qu’il faut bien voir que la psychanalyse ça fait quelque chose, à la langue, au corps, et la pratique de la psychanalyse comme toute activité du symbolique ça transforme, puisque le Symbolique transforme, l’enfant au moment du trauma quand il commence à rentrer dans la parole et bien la parole va transformer son corps, c’est grâce à ça qu’il va sortir de sa débilité, de sa prématuration et c’est pas un processus naturel, 22.57, donc il faut absolument couper ça, faire une coupure entre l’Imaginaire et le Symbolique, ça n’a rien d’Imaginaire et de naturel, c’est justement quelque chose qui va transformer le corps, ce qui me fait dire que ça transforme le corps c’est que le sujet autiste, c’est-à-dire l’enfant qui refuse de rentrer dans ce jeu de dupes qui s’appelle la Parole, qui n’est pas une simple posture imaginaire, qui va avoir une dimension d’autorité, mais qui ressemble beaucoup à la posture imaginaire sexuelle de la parade animale, c’est même pour ça qu’on confond beaucoup les choses, Lacan va .., c’est-à-dire que les animaux parlent, et ils parlent sans jamais ni écrire ni lire, il le dit aussi du Dieu de la nature, il dit que c’est Là que Aristote se trompe,... JMV16062015
|
||||||||||||||||||||||||||||||||||||||||||||
Syntaxe |
✔ |
la syntaxe, c’est le fait de découper et à partir de là, et là de voir qu’effectivement on peut s’orienter dans un ordre, et la syntaxe, le mot syntaxe, ça veut dire l’ordre, donc la syntaxe, c’est seulement l’aspect syntaxique que vous retrouvez en arithmétique, même en algèbre, même en logique, voyez ça, ( au tableau) ça c’est le fruit de certaines clauses formatives qui sont des clauses formatives dans les systèmes que Smullyan appelle formels, mais que moi j’appelle système d’écriture, parce que je pense que la forme c’est un mot qu’il faudrait bannir, parce que on s’est tellement gargarisé avec formalisation, formel, pourquoi dire qu’on veut formaliser, il y a des gens qui disent que moi, je veux formaliser la psychanalyse, pas du tout, moi, dans la psychanalyse, je pratique une écriture et même mathématique, et il y a une syntaxe, et j’invente même une nouvelle syntaxe pour la logique, pour faire le nœud logique, et que le nœud logique il ne pose pas de grands problèmes de nœuds, il est un plongement de la logique classique dans une logique plus grande, dans une Algèbre de Boole plus grande, JMV23062015 - Cours de Greg.LESSARD, 1996, 2016, Introduction à la linguistique, 2, |
||||||||||||||||||||||||||||||||||||||||||||
Système d'écriture ↑ |
✔ |
- Les systèmes d'écriture sont des Langage symboliques (Carnap), ou langues formulaire (Frege et Claude Imbert) qui s'opposent à la Phénoménologie, et aux USA c'est devenu les Systèmes formels (le paradigme Formel, forme, s'oppose à la matière, lieu d'un involution entre Spinoza et Marx, ce dernier faisant de la comptabilité via un Système d'écriture) |
||||||||||||||||||||||||||||||||||||||||||||
| S0T0, S1T1, S2T2, S3T3, S4T4 | - S0T0, S1T1, S2T2, S3T3, S4T4 (Système ou Syntaxe, Théorie), - Système formel pour Smullyan, que JMVappereau appelle Système d'écriture |
|||||||||||||||||||||||||||||||||||||||||||||
| Voir items Forme, Formel, - SPINOZA, l'Ethique, - Le concept de forme dans la philosophie de Spinoza, Yedfa OFRATH, 2014, Cairn.info, Le concept de forme ... avec ses dérivés (« former », « formel», etc.), apparaît à cent vingt-sept occurrences dans les écrits de Spinoza . |
||||||||||||||||||||||||||||||||||||||||||||||
| Système formel | ✔ |
- Système formel pour Smullyan, que JMVappereau appelle Système d'écriture | ||||||||||||||||||||||||||||||||||||||||||||
| T | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
Tables de noeuds
voir |
✔ | - voir, Taits, & .pdf, On knots III, par Peter GUTHRIE,
- Terminologie pour les Chaines et les Noeuds alternables, de 1 à 3 ronds, - |
 |
↑ | ||||||||||||||||||||||||||||||||||||||||||
- Théorie des tresses et entrelacs, planete sciences,
- Logiciens, Mathématiciens des noeuds et chaines, gaogoa - Noeuds et invariants, - Clinica de los processos del nudo, JMV, |
||||||||||||||||||||||||||||||||||||||||||||||
Table de vérité |
✔ |
- Une table de vérité est une table mathématique utilisée en logique classique — en particulier le calcul propositionnel classique et l'algèbre de Boole — pour représenter de manière sémantique des expressions logiques et calculer la valeur de leur fonction relativement à chacun de leurs arguments fonctionnels (chaque combinaison de valeur assumée par leurs variables logiques). Les tables de vérité peuvent être utilisées en particulier pour dire si une proposition est vraie pour toutes les valeurs légitimement imputées, c'est-à-dire : si une proposition est « logiquement valide ». W,
|
||||||||||||||||||||||||||||||||||||||||||||
Taits |
✔ |
- la première table de nœuds, c’est un écossais qui a fait ça, c’est Taits, qui est un élève de lord Kelvin, et la tentative de construire une table de nœuds, c’est une idée de lors Kelvin, puisque lui pensait remplacer par les relations entre nœuds pour les relations dans la Table de Mendeleïev sur les relations entre les éléments chimiques, il pensait que les nœuds étaient un modèle pour construire un autre type de théorie des éléments | ||||||||||||||||||||||||||||||||||||||||||||
Tarski |
✔ |
- Tarski sur Wiki (théorie des modèles et théorie sémantique de la vérité) - le prédicat de vérité : "la neige est blanche" est vrai, si et seulement si la neige est blanche - L'amour du tout aujourd'hui, 1ere partie , la fonction phallique, Cs et Ics avec Wundt, Tarski - voir Métalangage, voir Prédicat de vérité, - l'essentialisme arrogant de Tarski : la vérité est la dualité de ce qui est vrai. (selon GIRARD.J-Y, in Le point aveugle, T2, Vers l'inperfection, ) |
||||||||||||||||||||||||||||||||||||||||||||
| Tau de Hilbert; | ✔ | - David Hilbert a introduit l'opérateur ε, qui à toute propriété P associe un objet εx.P(x) tel que, si P est vérifiée par au moins un élément, alors P est vérifiée par εx.P(x). Cette construction permet de définir les quantificateurs et elle est utilisée par Nicolas Bourbaki pour développer sa théorie des ensembles, avec une variante notationnelle utilisant la lettre τ (tau), in, Axiome du choix, - je vous l’ai écrit ici à partir d’un exposé de Petitot, d’un exposé qu’il a fait à l’Ecole Freudienne en 1970, un exposé dans lequel il montre , lui il fait la même chose que ce que je vous propose d’écrire, mais il fait ça lui avec le Tau de Hilbert !, hors il faut savoir que le Tau de Hilbert c’est quelque chose qui a disparu après la guerre quand la logique s’est déplacée d’Europe vers les Etats-Unis, et qu’on vu disparaître ce qui semblait à certains mathématiciens ce qui semblait trop cabalistique, c’est-à-dire la manière dont Hilbert écrivait la théorie des ensembles, comme c’est le cas, bon si vous voulez voir ce qu’était le Tau de Hilbert, in Langage et linguistique, JMV,10092013, p9... - in JMV in LACAN, Séminaire XXVI, TT15051979, page 16, |
||||||||||||||||||||||||||||||||||||||||||||
Tautologie
|
✔ |
- en Logique Formelle : Proposition identique, dont le sujet et le prédicat sont un seul et même concept (exprimé ou non par un même mot). - en Logique Modale : Proposition qui reste vraie en vertu de sa forme seule, quelle que soit la valeur de vérité des propositions qui la composent ( selon Wittgenstein ). (CNRTL) (voir Ecole de Vienne) - Clef pour la passe, 2 eme partie, dans L'amour du tout, JMV, analyse des tautologies - Une Tautologie est un énoncé qui possède toujours la valeur de vérité vrai, quelle que soient les valeurs de vérité des propositions qui la composent.C'est le principe du Tiers Exclu. Voir Logique : La proposition; |
||||||||||||||||||||||||||||||||||||||||||||
Temps |
✔ |
- la topologie c'est le temps ! - Il y a une correspondance entre la topologie et la pratique. Cette correspondance consiste en les temps. La topologie résiste, c’est en cela que la correspondance existe. TT21111978, - Le temps logique et l'assertion de certitude anticipée, un nouveau sophisme, Ecrits p197, Lacan - Réduction du temps logique au cas classique, 1ere partie, JMV, (SEPARATION) - Le temps logique, - le séminaire XXVI, la topologie et le temps, |
||||||||||||||||||||||||||||||||||||||||||||
| Texte | - C'est pas les textes qui sont nocifs, c'est la façon dont on les publie, dont on les commente, dont on les utilise, qui l'est ! | |||||||||||||||||||||||||||||||||||||||||||||
Théorème ↑ |
✔ |
- Proposition "vraie" dans une théorie, proposition qui peut y être démontrée à partir d'axiomes. Dedelicq570 - Un théorème est une affirmation ou une proposition que l’on peut démontrer au travers d’un raisonnement logique fondé sur les axiomes. |
||||||||||||||||||||||||||||||||||||||||||||
Théorème de Lacan ↑ |
✔ |
- - 4 ≠3, discours entre groupe et foule, 1993-2007, - Démonstration du théorème majeur de Lacan, JMV, 02052012, |
||||||||||||||||||||||||||||||||||||||||||||
Théorie ↑ |
✔ |
- Ensemble d'énoncés et de définitions systématiquement organisés.Dedelicq571 - voir Théorème |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| Théorie axiomatique des corps commutatifs, | ✔ |
En mathématiques, un corps commutatif (parfois simplement appelé corps, voir plus bas, ou parfois appelé champ) est une des structures algébriques fondamentales de l'algèbre générale. C'est un ensemble muni de deux opérations binaires rendant possibles les additions, soustractions, multiplications et divisions. Plus précisément, un corps commutatif est un anneau commutatif dans lequel l'ensemble des éléments non nuls est un groupe commutatif pour la multiplication. Selon la définition choisie d'un corps qui diffère selon les auteurs (la commutativité de la multiplication n'est pas toujours imposée), soit les corps commutatifs sont des cas particuliers de corps (dans le cas où la commutativité n'est pas imposée), soit la dénomination corps commutatif est un pléonasme qui désigne simplement un corps (dans le cas où elle l'est). On renvoie à l'article corps (mathématiques) pour plus de détails. Des exemples élémentaires de corps commutatifs sont le corps des nombres rationnels noté La théorie des corps commutatifs est le cadre historique de la théorie de Galois, une méthode d'étude qui s'applique en particulier aux corps commutatifs et aux extensions de corps, en relation avec la théorie des groupes, mais s'étend aussi à d'autres domaines, par exemple l'étude des équations différentielles (théorie de Galois différentielle), ou des revêtements. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Théorie de l'asile
|
✔ |
- Noeud p 301 - Treillis "augmenté" des huit théories de l'asile, |
||||||||||||||||||||||||||||||||||||||||||||
Théorie algébrique des noeuds |
✔ |
- voir Lickorish, | ||||||||||||||||||||||||||||||||||||||||||||
Théorie des catégories |
✔ |
- Elle étudie les stuctures mathématiques, et les relations qu'elles entretiennent entre elles. L'étude des catégories, très abstraite, fut motivée par l'abondance de caractéristiques communes à diverses classes liées à des structures mathématiques. Les catégories sont utilisées dans la plupart des branches mathématiques et dans certains secteurs de l'informatique théorique et en mathématiques de la physique. Elles forment une notion unificatrice. - voir Catégories, ci-dessus, |
(wiki) |
|||||||||||||||||||||||||||||||||||||||||||
| Théorie de la démonstration, | ✔ | La théorie de la démonstration, aussi connue sous le nom de théorie de la preuve (de l'anglais proof theory), est une branche de la logique mathématique. Hilbert a proposé cette nouvelle discipline mathématique lors de son célèbre exposé au 2e congrès international des mathématiciens en 1900 avec pour objectif de démontrer la cohérence des mathématiques. Cet objectif a été invalidé par le non moins célèbre théorème d'incomplétude de Gödel en 1931, ce qui n'a toutefois pas empêché la théorie de la démonstration de se développer, notamment grâce aux travaux de Jacques Herbrand et de Gerhard Gentzen. Ce dernier a démontré l'un des résultats principaux de la théorie de la démonstration, connu sous le nom de Hauptsatz (théorème principal) ou théorème d'élimination des coupures. Gentzen a ensuite utilisé ce théorème pour donner la première démonstration purement syntaxique de la cohérence de l'arithmétique. ...... la théorie de la démonstration a connu une renaissance spectaculaire au cours des années 1960 avec la découverte de la correspondance de Curry-Howard qui a exhibé un lien structurel nouveau et profond entre logique et informatique : essentiellement, la procédure d'élimination des coupures définie par Gentzen peut être vue comme un processus de calcul, si bien que les démonstrations formelles deviennent alors des programmes dont le type est la proposition à démontrer. Depuis, la théorie de la démonstration s'est développée en étroite symbiose avec d'autres domaines de la logique et de l'informatique théorique, notamment le lambda-calcul, et a donné naissance à de nouveaux modèles du calcul, le plus récent étant la logique linéaire de Jean-Yves Girard en 1986. Aujourd'hui, une partie de la théorie de la démonstration se confond avec la sémantique des langages de programmation et interagit avec de nombreuses autres disciplines de la logique ou de l'informatique théorique |
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
|
↑ | |||||||||||||||||||||||||||||||||||||||||||||
| - Recherche sur la théorie de la démonstration, HERBRAND.Jacques, 1930, | ||||||||||||||||||||||||||||||||||||||||||||||
| - Théorie de la démonstration, GIRARD.Jean-Yves, | ↑ | |||||||||||||||||||||||||||||||||||||||||||||
Théorie |
✔ |
- voir Ensemble, ci-dessus, - Les diverses théories formalisées des ensembles [ La théorie des types de Whitehead et Russel, la théorie des ensembles ZF, de Zermelo-Fraenkel (ensembles ), S0T0; la théorie des classes de Von Neumann, Bernay et Gödel (ensembles et classes) ] apparaissent avec le temps comme diverses expressions d'une même réalité mathématique. - Hintikka montre un contre exemple de la démonstration de Quine, son livre de 1950 (Méthode de logique) , que la complétude de ses calculs qui sert à écrire toutes les mathtématiques, et y compris la théorie des ensembles , il a cru démontrer que le système des prédicats du premier ordre quantifié était complet. Hintikka montre en 1996 dans son livre Revisitation, 1996, traduit en 2007, qu'il faut rajouter un caractère, car ce n'était pas complet et dans son livre Les principes de mathématiques revisités, Hintikka propose une logique douce, friendly, et cette invalidation que le calcul des prédicats du premier ordre est incomplet contre la position de Quine, qui en faisait un argument fort pour pour adopter une attitude isolationniste depuis les années 1950, jusqu'en 1960 ou il vient au Collège de France et publie La philosophie de la logique qui repose sur une pétition de principe que sa logique est élégante et simple, consistante et complète, sans paradoxe, c'est ce que révèle Hintikka. Quine a milité pour que l'on abandonne tout intérêt pour les autres logiques, non classiques, non standard, |
||||||||||||||||||||||||||||||||||||||||||||
Théorie des ensembles de Morses-Kelley, MK
|
✔ | - La théorie des ensembles de Morse-Kelley (parfois abrégée en MK) est une théorie axiomatique exprimée en premier ordre dont les objets sont des classes, c'est-à-dire des ensembles en un sens proche de celui de la théorie des ensembles de Zermelo-Fraenkel (ZFC) mais aussi des « collections » d'ensembles ayant une même propriété, qui ne peuvent être considérés comme des ensembles sous peine de paradoxe, comme la collection de tous les ensembles. En cela elle est similaire à la théorie des ensembles de von Neumann-Bernays-Gödel (NBG), et se différencie de la théorie de Zermelo-Fraenkel qui ne permet de parler d'une classe qui n'est pas un ensemble que via la meta-théorie, par la propriété qui la définit. Cependant la théorie de von Neumann-Bernays-Gödel ne permet de définir des classes dans l'univers ensembliste que par des propriétés qui elles-mêmes sont définies en termes d'ensembles ; cette restriction du schéma d'axiomes de compréhension (pour les classes) fait de NBG une théorie finiment axiomatisable, et qui démontre les mêmes énoncés purement ensemblistes que la théorie de Zermelo-Fraenkel. La théorie de Morse-Kelley lève cette restriction : toute propriété exprimée dans le langage de la théorie définit une classe dans l'univers ensembliste, c'est alors une extension propre de la théorie des ensembles usuelle ZFC.
La théorie doit son nom aux mathématiciens Anthony Morse (en) et John L. Kelley, ce dernier ayant été le premier à en publier une version en appendice de son livre General topology, sous le nom de théorie de Skolem-Morse. La possibilité de lever la restriction au schéma de compréhension de la théorie des classes von Neumann avait été envisagée également, outre Skolem, par Quine et d'autres. Fraenkel, Bar-Hillel, et Levy, dans un livre paru en 1958 qui discute des différentes approches de la théorie des ensembles, la nomment système de Quine et Morse, et en attribuent la paternité également à Hao Wang. |
- Z, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
Théorie des ensembles NBG NBG Théorie des classes, |
✔ | - La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente1 à la théorie ZFC de Zermelo-Fraenkel avec axiome du choix (et avec les mêmes variantes possibles), mais dont le pouvoir expressif est plus riche. Elle peut s’énoncer en un nombre fini d’axiomes, et donc sans schéma, au contraire de ZFC (voir schéma d'axiomes de compréhension et schéma d'axiomes de remplacement). Ceci n’est possible que grâce à une modification du langage de la théorie, qui permet de parler directement de classe, une notion par ailleurs utile en théorie des ensembles et qui apparaissait déjà, de façon assez informelle, dans les écrits de Georg Cantor dès avant 1900.
La théorie des classes a été introduite en 1925 par John von Neumann, mais celui-ci avait pris des fonctions pour objets primitifs2. Elle est reformulée en termes de théorie des ensembles et simplifiée par Paul Bernays vers 19293. Kurt Gödel en donne une version inspirée de celle de Bernays, pour sa preuve de cohérence relative de l'axiome du choix et de l'hypothèse du continu par les constructibles, lors de conférences à Princeton en 1937-1938 (publiées en 1940). Une théorie des classes plus forte, la théorie de Morse-Kelley, a été proposée plus tard par plusieurs mathématiciens, et apparaît pour la première fois en 1955 dans le livre de topologie générale de John L. Kelley. |
- W, |
|||||||||||||||||||||||||||||||||||||||||||
Théorie des ensembles version ZF ↑ |
✔ |
- La théorie des ensembles ZF, est une partie de la théorie des ensembles, - La théorie de Zermelo et Fraenkel est une théorie égalitaire du premier ordre (/ aux théories d'ordre supérieur) dont les formules ne comportent - outre l'égalité- qu'un symbole de prédicat binaire noté ∈(appartient) . (binaire car d'arité 2). - La théorie axiomatisée des ensembles par J-M.Vappereau, - voir aussi ZF ci-desssous, |
||||||||||||||||||||||||||||||||||||||||||||
Théorie de l'évanouissement ↑ |
✔ |
- L'amour du tout, JMV, 1992, Elements formels pour une logique modifiée, Annexes théorie de l'avanouissement | ||||||||||||||||||||||||||||||||||||||||||||
| Théorie d'EVERETT | ✔ |
-La théorie d'Everett, appelée parfois théorie des états relatifs, théorie des mondes multiples (many-worlds) ou théorie des observateurs multiples (many-minds), est une formulation de la mécanique quantique fondée uniquement sur l'évolution déterministe de l’équation de Schrödinger, qui, appliquée à l’univers entier, régit son état quantique.
En effet, dans la formulation et l’interprétation conventionnelle de la mécanique quantique, un état quantique peut évoluer fondamentalement selon deux manières :
|
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
| Théorie des graphes, | ✔ |
- Théorie des graphes, Les algorithmes élaborés pour résoudre des problèmes concernant les objets de cette théorie ont de nombreuses applications dans tous les domaines liés à la notion de réseau (réseau social, réseau informatique, télécommunications, etc.) et dans bien d'autres domaines (par exemple génétique) tant le concept de graphe, à peu près équivalent à celui de relation binaire (à ne pas confondre donc avec graphe d'une fonction), est général. De grands théorèmes difficiles, comme le théorème des quatre couleurs, le théorème des graphes parfaits, ou encore le théorème de Robertson-Seymour, ont contribué à asseoir cette matière auprès des mathématiciens, et les questions qu'elle laisse ouvertes, comme la conjecture de Hadwiger, en font une branche vivace des mathématiques discrètes. |
W, |
|||||||||||||||||||||||||||||||||||||||||||
| et topologie, | ↑ | |||||||||||||||||||||||||||||||||||||||||||||
Il existe trois grandes familles de graphes et cinq catégories au total :
|
||||||||||||||||||||||||||||||||||||||||||||||
| - Voir ESSAIM, JMV, Chapitre I, Chapitre II, Annexe, |
||||||||||||||||||||||||||||||||||||||||||||||
Théorie des groupes |
✔ |
En mathématique, plus précisément en algèbre générale, la théorie des groupes est la discipline qui étudie les structures algébriques appelées groupes. Le développement de la théorie des groupes est issu de la théorie des nombres, de la théorie des équations algébriques et de la géométrie. La théorie des groupes est étroitement liée à la théorie des représentations. Ensemble, elles ont plusieurs applications en physique théorique, chimie, science des matériaux et cryptographie asymétrique. L'une des plus grandes avancées mathématiques du XXe siècle est la classification complète des groupes simples finis. Elle est le fruit d'une collaboration de plus de 100 auteurs à travers 500 articles |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Groupe, |
- Axiomatiquement un groupe est : un ensemble muni d'une loi de composition interne (x,y) -->x*y associative, telle qu'il existe un élément privilégié e, appelé élément neutre, tel que x*e = e*x = x et tel que tous les éléments aient un inverse (c-à-d que pour tout x il existe un élément y tel que x*y = y*x = e). Un tel groupe est dit abélien ou commutatif, si x*y = y*x . (Dictionnaire des mathématiques, T1, p14, EU, Albin MICHEL), plus simplement une définition du groupe se résume en la formule suivante : |
|||||||||||||||||||||||||||||||||||||||||||||
Structure de groupe, |
Structure la plus simple et la plus importante des mathématiques ! Structure qui jouerait un rôle dans les mécanismes de la pensée ! et préexisterait dans notre esprit, la géométrie ne se concevant pas sans elle ! - définition simple du groupe (& voir ci-dessus) : Ensemble d'éléments munis d'une loi commune, & interne, autres définitions voir ci-dessus. |
|||||||||||||||||||||||||||||||||||||||||||||
| Les ensembles usuels de nombres ( entiers, relatifs, rationnels, complexes) sont des groupes abéliens pour l'addition; | ||||||||||||||||||||||||||||||||||||||||||||||
| Les ensembles des nombres rationnels non nuls, ou réels non nuls, sont des groupes abéliens pour la multiplication, | ||||||||||||||||||||||||||||||||||||||||||||||
| L'espace à trois dimensions (3D) est un groupe non commutatif car ses transformations conservent la distance de deux points dans les déplacements. Ce dans la géométrie euclidienne. (la topologie subvertie cette "rigidité" métrique ..!) | ||||||||||||||||||||||||||||||||||||||||||||||
Théorie à homotopie
(mouvements gordiens propre) près, H,
|
✔ |
- pour Soury, dans la théorie à homotopie ( mouvements gordiens propre) près, H, où ne subsiste que des chainettes borroméennes à homotopie près ( chaines finkéennes qui intéressent le calcul de Milnor), théorie de la névrose et du nom du père om le désir est perversement orienté selon Lacan. Le Bog ne disparait pas dans le théorie à mouvement noeud propre près. | ||||||||||||||||||||||||||||||||||||||||||||
| Théorie de l'informatique | -Le terme informatique fut crée (en 1962 par Philippe Dreyfus) par la réunion des deux termes information et automatique. Il s'agit du traitement automatique de l'information. L'une des traditions dans lesquelles l'informatique puise une partie de sa force est celle de l'automatisme. Un automate est une machine imitant les mouvements, les fonctions ou les actes d'un corps animé. Les premiers automates répondaient au principe de programmation, c'est-à-dire d'exécution d'une séquence finie d'évènements, (voir la technique de l'arbre à cames). L'information analogique a comme support un signal continu, une oscillation dans une ligne électrique par exemple. L'information digitale désigne l'information codée de façon symbolique par des chiffres (par exemple, décimaux). Les ordinateurs traitent des informations digitales codée en base 2 (binaire). Le message transmis est alors constitué par des successions (ou paquets) de chiffres, sous forme de signaux binaires. Ce que l'on appelle la théorie de l'information, (Claude Shannon, 1948), fournit une mesure de quantité d'information dont l'unité est le "le bit" (Binary digIT ; digit = nombre d'où digitaliser = numériser). Le Bit, c'est la quantité d'information contenue dans le choix élémentaire entre deux possibilités également probables, comme dans le cas du lancer d'une pièce de monnaie pour obtenir pile ou face. L'une des premières utilisation du code binaire par une machine fut le métier à tisser de Jacquard. Joseph Marie Jacquard (1752-1834) construisit en 1804 le premier métier à tisser entièrement automatique commandé par un système de cartes perforées : un tambour mobile soulève des crochets. Les trous -ou leur absence- sur les cartons qui défilent interviennent directement sur la position des fils de chaîne au moment du passage du fil de trame, commandant ainsi le motif du tissu. suite sur le site Jussieu, ci-contre,
|
- Jussieu, |
||||||||||||||||||||||||||||||||||||||||||||
| - voir Informatique théorique, ci-dessus, | ||||||||||||||||||||||||||||||||||||||||||||||
| - voir Automate, automate mécanique, automate d'art, sources wikipedia, | ||||||||||||||||||||||||||||||||||||||||||||||
| - voir Automatique, | ||||||||||||||||||||||||||||||||||||||||||||||
| - Engin de siège dans l'Antiquité romaine, et automatisme, sur wikipedia, | ||||||||||||||||||||||||||||||||||||||||||||||
| Dei ex Machinis : Jean-Arcady MEYER , 2015, Editions du Net, VolumesI , – De l'Antiquité à Hans Schlottheim, Volume II – De Salomon de Caus à Johann Nepomuk Maelzel , Volume III – De Jean-Baptiste Schwilgué au milieu du XXe siècle, |
||||||||||||||||||||||||||||||||||||||||||||||
Théorie de la kantification↑ |
✔ |
- Elle croise les régimes de la coordination des concepts et des propositions - Présentation des formules kantique de la sexuation, table des matières, dans IV, SEPARATION, Formules de la sexuation et 6 annexes logiques. JMV |
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
| Théorie des modèles | ✔ | - La théorie des modèles est une branche de la logique mathématique qui traite de la construction et de la classification des structures. Elle définit en particulier les modèles des théories axiomatiques, l'objectif étant d'interpréter les structures syntaxiques (termes, formules, démonstrations...) dans des structures mathématiques (ensemble des entiers naturels, groupes, univers...) de façon à leur associer des concepts de nature sémantique (comme le sens ou la vérité). | W, |
|||||||||||||||||||||||||||||||||||||||||||
| La théorie des modèles est une branche de la logique mathématique. Son principe de base est qu’une théorie est mathématiquement valide si on peut définir un univers dans lequel elle est vraie. | ||||||||||||||||||||||||||||||||||||||||||||||
| Théorie des mondes possibles, | ✔ |
- Les théories des mondes possibles sont des théories élaborant la possibilité qu'existent d'autres mondes que le nôtre. Elles sont issues de la sémantique de Kripke qui est à l'origine de nombreuses réflexions métaphysiques. D'abord théorisé par Leibniz, le concept de « mondes possibles » a fait l'objet d'un intérêt renouvelé, au XXe siècle, grâce aux travaux de la logique modale, portant sur la nécessité, la possibilité et la contingence, et en particulier grâce à la sémantique des mondes possibles développée dans les années 1950 par Saul Kripke, Stig Kanger et Jaakko Hintikka. | W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
Théorie de la mémoire |
✔ |
- voir Rêve, et clef des songes, in Hadrian Bibliothèque, gaogoa, Item Rêve, Oracles, Magie, - Théorie de la mémoire, GATAPAC.Antoine, 1866, Bnf-Gallica, & TdM, - Matière et mémoire, BERGSON, Essai sur la relation du corps et de l'esprit, 1939, UQAC, Table des matières, - Mémoire et Inconscient, Item Inconscient sur cette page. - Langage et Ecritures, gaogoa, - - L'art de la mémoire, Yate Frances, : Ainsi, manuscrits, abbayes, églises, cathédrales étaient-ils à lire en établissant des correspondances pour soi-même. On était invité à traiter toutes ces fictions de pierre, d’image et de liturgie comme une série de loci qui pouvaient entrer en résonance mnémonique avec la grâce et la parole divine. |
||||||||||||||||||||||||||||||||||||||||||||
- la mémoire dépend de la syntaxe, et n'est pas sans sujet ! ( JMV23062015) |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
Théorie des modes du semblant |
- - ? |
|||||||||||||||||||||||||||||||||||||||||||||
Théorie à mouvement noeud popre près |
✔ |
- La théorie à mouvement noeud popre près.... - le Bog ne disparait pas dans la théorie à mouvement noeud popre près. (re) in Noeud borroméen généralisé, ci-dessus, |
||||||||||||||||||||||||||||||||||||||||||||
Théorie des noeuds↑ |
✔ |
- Il n 'y a pas de théorie des noeuds (en 2014), - Théorie des noeuds ..., JMV16062015, - Terminologie des Chaines et Noeuds alternables. - Théorie des noeuds selon Wiki, - une petite introduction sur les Noeuds, de Jérôme DUBOIS qui rejoint celle des Champs du noeud sur gaogoa, |
||||||||||||||||||||||||||||||||||||||||||||
Théorie des noeuds classique |
✔ |
- Théorie classique des noeuds Bourbaki, Gramin, - Théorie des noeuds classique : c'est la théorie des noeuds physiques, faits avec de la corde, ils peuvent être déformés sans changer leur identité par les composés des trois mouvements de Reidmaster, T1, B2, T3." ça claque ", p61, 2008, JMV |
||||||||||||||||||||||||||||||||||||||||||||
Théorie des noeuds à mouvement gordien (impropre) près, G, |
✔ |
- Dans le Treillis des huit théories de l'asile, le Bog est défait par les deux théories G et H. Pour Lacan, dans la Théorie de noeuds à mouvement gordien (impropre) près, G, ou ne subsistent que des noeuds propres et des enlacements, théorie de la psychose parnaoïaque, et de l'élément qui est sinthome et névrotique (enlacements), | ||||||||||||||||||||||||||||||||||||||||||||
Théorie des nombres |
✔ |
- voir Nombre ci-dessus,
|
||||||||||||||||||||||||||||||||||||||||||||
Théorie des nombres : Le terme « arithmétique » est aussi utilisé pour faire référence à la théorie des nombres. C'est un terme assez ancien, qui n'est plus aussi populaire que par le passé ; pour éviter des confusions, on désignait aussi parfois, jusqu'au début du vingtième siècle, la théorie des nombres par le terme « arithmétique supérieure ». Néanmoins, l'adjectif arithmétique reste assez répandu, en particulier pour désigner des champs mathématiques (géométrie algébrique arithmétique, arithmétique des courbes et surfaces elliptiques, etc.), où la restriction des questions et des solutions aux entiers, ou à certaines de leurs extensions, joue un rôle déterminant. Ce sens du terme arithmétique ne doit pas être confondu avec celui utilisé en logique pour l'étude des systèmes formels axiomatisant les entiers, comme dans l'arithmétique de Peano. La théorie des nombres est divisée en plusieurs champs d'étude en fonction des méthodes utilisées et des questions traitées
|
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
| Ordinaux et cardinaux, | ↑ | |||||||||||||||||||||||||||||||||||||||||||||
moi je tiens que l’écriture des nombres par position qui est effectivement parfaite au sens où chaque nombre a une seule écriture, une seule expression, il n’y a pas de double, et n’y a pas d’omission, on peut construire tous les ordinaux à partit des axiomes de Penao, vous avez l’axiomatisation des nombres entiers et vous pouvez écrire tous les nombres entiers en les écrivant grâce à un système numérique d’écriture, système d’énumération, de numération ?, qui est excellent, qui produit tous les ordinaux d’une manière absolument parallèle, c’est un duplicate dans l’écriture de ce qu’on peut dire des nombres à partir du moment où on a appris à compter !
Mais il y a les nombres cardinaux, et les enfants apprennent d’abord les nombres cardinaux, dans leur découverte, dans leur réinvention de la langue, il découvre d’abord les cardinaux, et il faut qu’ils apprennent à compter pour découvrir les ordinaux, mais moi je tiens que l’alphabet, l’écriture alphabétique, je parle d’une idéologique, mais Derrida, dans la Grammatologie, parle d’un logocentrisme occidental, c’est lié à cette écriture alphabétique de la langue, vous voyez que toutes les langues ne s’écrivent pas avec des alphabets, ce qui est bien connu c’est le chinois, mais aussi le japonais qui emprunte ses caractères, ses lettres au chinois, ce ne sont pas des caractères, ce sont des lettres, ce ne sont pas des lettres d’un alphabet, et puis vous avez les hiéroglyphes Champollion, qu’il va apprendre à lire, il va en réinventer la lecture, puisqu’il n’en a pas le signifiant, il ne sait pas comment on parlait, il arrive quand même à lire grâce à trois version du même texte, donc là on est à l’orée de la psychanalyse avec Champollion, comment lire un rêve qui n’est pas écrit de manière alphabétique, c’est même à mon avis le pourquoi de ce qu’on étudie plus beaucoup les rêves, on en parle pas beaucoup, ce qui est formidablement inquiétant, je pense que dans une société, ou une école professionnelle, il devrait y avoir un enseignement de Champollion, comment est-il arrivé à décrypter la pierre de Rosette, parce que les rêves c’est aussi compliqués ! JMV ? |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
| Théorie de Skolem-Morse | ✔ | - C'est la théorie des ensembles de Morse-Kelley - La théorie doit son nom aux mathématiciens Anthony Morse (en) et John L. Kelley, ce dernier ayant été le premier à en publier une version en appendice de son livre General topology, sous le nom de théorie de Skolem-Morse. La possibilité de lever la restriction au schéma de compréhension de la théorie des classes von Neumann avait été envisagée également, outre Skolem, par Quine et d'autres. Fraenkel, Bar-Hillel, et Levy, dans un livre paru en 1958 qui discute des différentes approches de la théorie des ensembles, la nomment système de Quine et Morse, et en attribuent la paternité également à Hao Wang. |
- W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
| Théorie des schémas | ✔ | - Un schéma est avant tout un objet géométrique. Telle qu'elle a été inventée, cette notion généralise la notion de variété algébrique. À une variété algébrique sur un corps, la théorie des schémas ajoute des points qui ne sont pas nécessairement fermés (grosso modo, ce sont des points dont les coordonnées sont des variables). En théorie des nombres, pour étudier les propriétés arithmétiques d'une variété algébrique V sur La notion de schéma est due à Alexandre Grothendieck, qui l'a inventée dans le but de démontrer les conjectures de Weil (qui sont maintenant un théorème, démontré par Pierre Deligne) vers l'année 1958. La théorie des schémas est développée dans le grand traité de fondements, inachevé (mais très complet !), les Éléments de géométrie algébrique, plus connu des mathématiciens sous le nom des EGA.
- et voir schéma,.... |
- W, - W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||
| Théorie des types | ✔ | FREGE : Russel critiquera la règle de compréhension non restreinte de Frege qui rendait sa théorie contradictoire (de même pour Cantor et la théorie des ensembles).
En 1902 Frege arrête de publier après avoir signalé l'objection de Russell (la critique de Russell deviendra la théorie des Types de Russell). Il abandonne l'écriture de son 3 eme volume et Il ne publiera plus que des travaux mineurs et il abandonne le logicisme en 1923 pour chercher une fondation des mathématiques sur la Géométrie. |
||||||||||||||||||||||||||||||||||||||||||||
| - La théorie des types est une branche de la logique mathématique : elle fonde la construction des objets sur la notion de fonction et non pas sur celle d'ensemble.
Une première théorie des types a été créée par Bertrand Russell pour résoudre les paradoxes de la théorie des ensembles ; lourde d'emploi, elle a été supplantée par la théorie de Zermelo-Frankel avant d'être réconsidérée après la découverte du lambda-calcul. En théorie des types, les entités mathématiques sont construites à l'aide de fonctions, où chaque fonction a un type qui décrit le type de ses arguments et le type de la valeur retournée. Les entités sont bien formées lorsque les fonctions sont appliquées à des entités ayant le type que la fonction attend. Le concept de type a plusieurs domaines d'applications :
|
|
↑ | ||||||||||||||||||||||||||||||||||||||||||||
- D'un point de vue de la théorie mathématique : les types ont été pour la première fois théorisés par Bertrand Russell comme réponse à sa découverte du paradoxe ébranlant la théorie naïve des ensembles de Gottlob Frege. Cette théorie des types est développée dans l'ouvrage Principia Mathematica de Russell et Whitehead. Elle permet de contourner le paradoxe de Russell en introduisant tout d'abord une hiérarchie de types, puis en assignant un type à chaque entité mathématique. Les objets d'un certain type ne peuvent être construits qu'à partir d'objets leur pré-existant (situés plus bas dans la hiérarchie), empêchant ainsi les boucles infinies et les paradoxes de surgir et de casser la théorie. Pour ce qui concerne le sous-domaine des mathématiques nommé la logique mathématique — mais c'est aussi très utile dans le domaine de l'informatique, dans des sous-domaines nommés théorie des grammaires, théorie de la compilation, et système de réécriture, voire plus récemment dans le domaine de la transcompilation — on utilise les types dans le cadre de la théorie des types. Dans le langage courant, « théorie des types » est à comprendre dans le contexte des systèmes de réécriture. L'exemple le plus connu est le lambda calcul d'Alonzo Church. Sa Theory of Types1 a permis de passer du calcul non-typé originel, incohérent du fait du paradoxe de Kleene-Rosser (en), à un calcul correct. Church a démontré que ce système pouvait servir de fondement des mathématiques ; on le décrit comme une logique d'ordre supérieur. |
- W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
Théorie de la vérifonctionnalité ↑
|
✔ |
- Théorie de la vérifonctionnalité qui régit la coordination entre concepts et propositions. |
||||||||||||||||||||||||||||||||||||||||||||
-Traite de la valeur de vérité de certains connecteurs logiques. -voir Vérifonctionnalité, ci-desssous, |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
Vérité |
- que p, c’est l’écriture de l’affirmation, qui n’est pas l’assertion, parce que l’assertion c’est 1, c’est le problème de la vérité chez Tarski, on verra que justement la définition du prédicat de vérité, ce qui l’amène à introduire le fait qu’il ne faut surtout pas que ce soit des langages sémantiquement clos, ça va être le fait qu’il y a encore une analyse insuffisante de la différence qu’il y a entre la vérité apophantique empirique, la vérité d’une proposition, et puis l’énonciation, l’assertion, la vérité logique, celui qui le dit mieux, même beaucoup mieux que Wittgenstein c’est Frege, Frege dit ça comme ça, il dit : ça ne sert à rien de dire que quelque chose est vrai parce que ça n’ajoute aucune vérité à la chose. JMV20150609 -voir ce mot ....ci-dessous; |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
Tiers Exclu |
✔ |
- Le principe du Tiers Exclu, c'est une Tautologie soit un énoncé qui possède toujours la valeur de vérité vrai, quelle que soient les valeurs de vérité des propositions qui la composent.voir La proposition, En logique, le principe du tiers exclu est équivalent à l'implication de la double négation ¬ ( ¬ p ) ⇒ p , |
W, |
|||||||||||||||||||||||||||||||||||||||||||
Voici des formulations équivalant au tiers-exclu, parmi les plus connues :
|
||||||||||||||||||||||||||||||||||||||||||||||
Timée |
✔ |
-Le Timée, PLATON | ||||||||||||||||||||||||||||||||||||||||||||
Topiques↑
|
✔ |
- - 1 er et 2 eme topiques de Freud, - voir appareil psychique |
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
Topologie↑ |
✔ | La topologie est une branche des mathématiques concernant l'étude des déformations spatiales par des transformations continues (sans arrachages ni recollement des structures).
- Elle étudie les propirétés locales d'un espace quelconque. |
- W, |
|||||||||||||||||||||||||||||||||||||||||||
Topologie algébrique ↑ |
✔ |
- La topologie algébrique peut être traitée comme un problème de mots écrits avec des grandes Lettres et des lettres minuscules. Problème qui relève de la théorie des graphes. Essaim p 54 |
||||||||||||||||||||||||||||||||||||||||||||
Topologie générale ou ensembliste ↑ |
✔ |
- Le terme de continu définit ce qui relève de la topologie. C'est à la topologie générale nommée aussi topologie ensembliste que revient la charge de définir les applications continues. Elle donne donc son cadre à la topologie dans son ensemble. Essaim p 27 - Fournit un vocabulaire et un cadre général pour traiter des questions de limites, de continuité, et de voisinage.(wiki) - La topologie générale, - voir Topologie sur wiki, - La topologie générale est une branche de la topologie qui étudie les propriétés des espaces topologiques et des structures définies sur ces ensembles. Contrairement aux autres notions de topologie, elle se distingue par son caractère plus universel, notamment pour les espaces topologiques. wikiversity, |
||||||||||||||||||||||||||||||||||||||||||||
La topologie en psychanalyse↑ |
✔ |
|
||||||||||||||||||||||||||||||||||||||||||||
& psychanalyse |
- La topologie est imaginaire. Elle n’a pris son développement qu’avec l’imagination. Il y a une distinction qui est à faire entre l’Imaginaire et ce que j’appelle le Symbolique. Le symbolique, c’est la parole. L’imaginaire en est distinct. Lacan, TT19121978, -
que les perceptions signes , "das Wahrnehmungsbewußtsein" , c'est des perceptions découpées, c'est pas des signes de perception, des perceptions qui deviennent signes du fait d'un découpage, lire c'est commencer par découper, et c'est pour ça que la topologie c'est basique, c'est élémentaire, c'est l'écriture et la langue mathématique inventée , pas toujours parfaitement foutue, JMV09092014 - Topologie et dimensions et mouvements, - La topologie, et la psychanalyse - histoire de la topologie, JMV20150602, - Gilson.J-P, La topologie ordinaire de J.Lacan, une articulation de la cure, Editions Balzac, L'ecriture indocile, 1994, ELM, 2, 3, -- Invariants pour les noeuds |
|
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
Topologie du sujet ↑ |
✔ |
- La topologie du sujet, - JMV20110104 : le : Il n’y a pas de rapport sexuel, mais le problème c’est que ça marche quand même, ça marche quand même, même pas bien, comme je l’ai dit de la topologie, à la Lettre lacanienne, c’est pas que c’est pas ça, c’est ça, mais à la gomme et jamais aux petits oignons, c’est ça la topologie, c’est ça qui les emmerde tous, il n’y a pas de maitrise, parce qu’il faut recommencer à chaque fois. - Sa matière est constituée par des séries de lettres, dont l'ordre peut être un graphe, ou celle de structures algébriques ou de structres topologiques. La structure de groupe les compose ! |
||||||||||||||||||||||||||||||||||||||||||||
Tore↑ |
✔ |
- Tore, étoffe bilatère de genre 1. Indicateur Eeuler Poincarré = 0, Groupe Fonfamental: G est Z². - Trou coupure, 2, |
||||||||||||||||||||||||||||||||||||||||||||
Trait unaire ↑ |
✔ |
- "Invention du trait unaire, à partir du trauma, du côté des oreilles, produit par le malentendu des parents qui ne s'entendent pas crier, ce trait sur lequel s'appuie l'identification, qui fournit l'intuition du sujet, d'être lu avant que de savoir l'écrire. Le lire est différent de sa conceptualisation. La poésie commence là. Le trait unaire est lisible dès cette étape, avant de devenir un écrit, une lettre qui elle dépend d'un discours, d'un lien social. C'est le signifiant des Nom du père, différent du Savoir supposé dont nous faisons sujet, jusqu'à la castration, comme manque dans l'Autre." ..Les incorporels des stoiciens complétées des Incorporelles de Lacan,..., effets de langage préalables à la signifiance du sujet ......JMV," ça claque ",p59, 2008, revue Essaim. C'est mieux que les propositions sur la signification de Quine. - le triskel, - Les noms du père, dont Marcel Mauss établit la liste dans son Manuel d'ethnographie , - qui comble la marque invisible que le sujet tient du signifiant et l'aliène dans l'identification première qui forme l'idéal du moi p808 Subversion du S, Ecrits - à propos du Trait unaire, lorsqu’il veut expliquer ce que c’est que le trait unaire, et le coup des encoches dans l’os, la fois suivante, il dit, nous avons fait une grande découverte : il faut savoir lire pour inventer une écriture, moi je tiens que c’est quelque chose d’absolument innovant .., JMV20150602 |
||||||||||||||||||||||||||||||||||||||||||||
Transfini
|
✔ |
- Synonyme d'infini dans le cas des nombres. Les nombres transfinis sont des nombres exposés et étudiés par le mathématicien Georg Cantor. Se fondant sur ses résultats, il a introduit une sorte de hiérarchie dans l'infini, en développant la théorie des ensembles. Un nombre entier naturel peut être utilisé pour décrire la taille d'un ensemble fini, ou pour désigner la position d'un élément dans une suite. Ces deux utilisations correspondent aux notions de cardinal et d'ordinal respectivement. Ces nombres ont des propriétés différentes selon que les ensembles auxquels ils s'appliquent sont finis ou infinis. Ces cardinaux et ordinaux sont dits transfinis dans le second cas. Leur existence est assurée par l'axiome de l'infini. Le premier nombre ordinal transfini est noté ω (oméga), dernière lettre de l'alphabet grec. L'addition des ordinaux est associative mais pas commutative. On peut aussi définir une multiplication et une exponentiation, ce qui donne lieu à une arithmétique sur les nombres ordinaux transfinis. Dans ZFC, la théorie des ensembles de Zermelo-Fraenkel avec axiome du choix, à tout ensemble correspond un cardinal, et les cardinaux sont deux à deux comparables ; dans ce cadre, le plus petit cardinal transfini est noté Il y a une arithmétique des cardinaux, qui est différente de celle des ordinaux. Le cardinal - Nombres NZQR, |
- א aleph - voir Cantor, sur chronomath, |
|||||||||||||||||||||||||||||||||||||||||||
Transcendance |
✔ |
- ça veut dire au delà, dépassement, -(JMV02092014-I,38.16) (2), |
||||||||||||||||||||||||||||||||||||||||||||
Transcendantal
|
✔ |
- la critique transcendantale, ce n'es pas transcendant, c'est pas le dépassement, c'est juste que nous avons une relation avec un objet, et j'ai une relation à la relation que j'ai avec cet objet, c'est-à-dire que je peux faire un commentaire, et si je fais un bon commentaire qui rejoint l'objet, si je joue de la musique, et si quelqu'un trouve que ce que je fais rejoint la musique, alors la critique va fonder la musique, JMV09092014, | ||||||||||||||||||||||||||||||||||||||||||||
Transfert |
✔ |
- dans Direction de la cure, dans le cas de Dora et de l’Homme au rat, il explique que les entretiens préliminaires, il ne faut pas s’occuper du transfert, il y a un transfert primaire, il faut parler avant de les allonger, de la position du sujet vis-à-vis de la langue, du Symbolique, et quand on est d’accord, qu’il ne s’agit pas d’une relation du Moi au monde, dans la psychanalyse, mais d’une relation du sujet à la langue, lié au langage, à ce moment là si on est d’accord là-dessus on peut lui refuser un regard, ça veut dire que c’est le moment où on peut allonger quelqu’un, JMV20150602, | ||||||||||||||||||||||||||||||||||||||||||||
Transmission ↑ |
✔ |
- on n'apprend que ce que l'on sait déjà
|
||||||||||||||||||||||||||||||||||||||||||||
Transparence↑ |
✔ |
- La LCC, in L'amour du tout aujourd'hui, 2 eme partie, JMV, 1992 | ||||||||||||||||||||||||||||||||||||||||||||
Traumatisme ↑ |
✔ |
- DI (ou la Dei)=trauma=le Phallus=la Parole=fonction phallique |
||||||||||||||||||||||||||||||||||||||||||||
Trèfles (famille des) ↑ |
✔ |
- Le noeud de trèfle, le 222-33 et le 3T : 33-222, |
||||||||||||||||||||||||||||||||||||||||||||
Treillis↑ ou Lattices |
✔ |
- Ensemble ordonné. (selon wiki). - Treillis des connecteurs logiques binaires, tentative d'écriture du 27012015 à l'ENS et cour de JMV du 27012015 - Un treillis c'est un hypercube. Et un hypercube c'est un tore. (un cube à l'intérieur d'un autre cube) - Treillis des huit théories dans l'asile, Noeud Chap VII, p 297, 301, JMV, - Treillis des 8 théories dans l'asile (enfermé dehors et dedans) augmenté !, |
||||||||||||||||||||||||||||||||||||||||||||
| Tresse | ✔ | - voir Entrelacs, Noeuds, Tresses, Chaines, Echeveau, sur gaogoa, - Alexander en 1923 explique l'importance des tresses dans la théorie des noeuds, on peut les obtenir tous ! Ce qui permet d'énoncer le théorème d'Alexander : Chaque noeud s'obtient de la cloture d'une certaine tresse . (En fait Alexander a démontré que cette assertion est vraie plus généralement pour les entrelacs, dont les noeuds sont un cas particulier.) d'après Noeuds, Alexei.SOSSINSKY, Seuil, p42, |
||||||||||||||||||||||||||||||||||||||||||||
Triangle arithmétique de Pascal ↑ |
✔ |
- En mathématiques , le triangle de Pascal est une présentation des coefficients binomiaux dans un triangle . Il fut nommé ainsi en l'honneur du mathématicien français Blaise Pascal . Il est connu sous l'appellation triangle de Pascal en Occident, bien qu'il fut étudié par d'autres mathématiciens des siècles avant lui en Inde , Perse , Maghreb , Chine (où il est appelé « Triangle de Yang Hui »), Allemagne et Italie . (source Wiki) - |
||||||||||||||||||||||||||||||||||||||||||||
Trieb |
✔ |
- voir Pulsion - Dérive, - comment parler à partir de là du Trieb ?, vous voyez que quand le symbolique tombe dans le corps, sur le corps, traverse le corps, il y a une très belle phrase de Lacan dans la Direction de la cure où il dit que c’est jamais simple, que le névrosé est pas mal placé dans l’être, parce qu’il se plaint de ce passage, le névrosé se plaint parce que pour lui c’est une peine, donc il n’est pas question de dire qu’il faut se satisfaire de cette peine, mais le fait est que c’est effectivement une peine pour le sujet de se trouver être l’agent qui fait entrer le symbolique dans le monde et c’est ensuite par ses actions et y compris par l’écriture qu’il va modifier le monde, qu’il va transformer le monde, nous sommes des sujets ségrégatifs parce que le signifiant a cette structure qui est celle déjà avec la parole ET ensuite avec l’écriture, le signifiant et la lettre ont toujours cette dimension de quelque chose qui se dédouble, 51.40, ça s’appelle la répétition freudienne, c’est ce que Freud va rencontrer dans les années 1920, c’est ce que Lacan appelle dans les Séminaires des années 1960, la grande différence, c’est cette pulsation qu’il y a à l’intérieur du symbolique, qui fait que c’est quelque chose qui n’a rien à voir avec la Nature, et même si ça va nous permettre d’inventer les machines , nous sommes la seule espèce animale qui inventons des machines, et même des machines électroniques, on a commencé par des machines à vapeur, on a même commencé par des outils, mais n’empêche que ça va nous permettre de construire des nouvelles machines, et c’est le fonctionnement de ce dédoublement et de cette identité, de cette pulsation qui fonctionne aussi dans nos machines mais qui fonctionne d’une manière spéciale dans le symbolique, c’est là qu’il faut distinguer le symbolique de l’ordre mécanique ou électronique, dans la mesure ou vous voyez bien que la machine peut reproduire des choses que vous lui apprenez à faire, mais elle ne va pas inventer ce que vous vous pouvez inventer si vous vous racontez des histoires, ou bien aussi des mathématiques, par exemple la découverte d’une démonstration en mathématique ne se fait pas d’une manière automatique, 52.58, JMV16062015 |
||||||||||||||||||||||||||||||||||||||||||||
Triskel, Quadriskel ↑ |
✔ |
- Triskel, - triskel, quadriskel, - voir Trait unaire, Nom du père, M.Mauss, point, - en grec triskelhs (triscèlès) signifie “à trois jambes”, comme isocèle (iso-scèle) désigne un triangle qui a “deux jambes égales”… |
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
Trivial↑ |
✔ |
- pas de noeud, p19 - |
||||||||||||||||||||||||||||||||||||||||||||
Trivialise↑ |
✔ | - s'efface, Noeud p20 - le différence s'efface dans l'identité, JMV09092014, 01.09.42 ; |
||||||||||||||||||||||||||||||||||||||||||||
Fibré, |
En mathématiques, un espace fibré est, intuitivement, un espace topologique qui est localement le produit de deux espaces — appelés la base et la fibre — mais en général pas globalement. Par exemple, le ruban de Möbius est un fibré de base un cercle et de fibre un segment de droite : il ressemble localement au produit d'un cercle par un segment, mais pas globalement comme le cylindre Plus précisément, l'espace total du fibré est muni d'une projection continue sur la base, telle que la préimage de chaque point soit homéomorphe à la fibre. Cette projection est a priori supposée localement triviale, c'est-à-dire que tout point de la base admet un voisinage dont la préimage s'identifie à un produit cartésien de ce voisinage et de la fibre, par le biais d'homéomorphismes appelés trivialisations ou cartes. Le passage d'une trivialisation à l'autre se fait au moyen d'un groupe d'homéomorphismes de la fibre appelé groupe de structure. Cette notion généralise donc la projection d'un produit cartésien sur l'un de ses facteurs. |
W, |
||||||||||||||||||||||||||||||||||||||||||||
Trou↑ |
✔ |
- Le vide est défini par l'ensemble vide |
||||||||||||||||||||||||||||||||||||||||||||
| U, | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
Un
|
✔ |
- Henologie, Science de l'Un, - ou pire..., Lacan - Définition des nombres pairs et impairs, je vous ai dit que 0 et 1 c’est la congruence modulo 2, donc c’est les nombres pairs et les nombre impairs, 0 c’est tous les nombres pairs, et 1 c’est tous les nombres impairs, donc si vous prenez 2 nombres impairs, 1+1 = 0, vous voyez bien que la somme de 2 nombres impairs ce sera toujours pair ! parce que une nombre impair c’est toujours une nombre pair plus ou moins un, un nombre impair on va l’appeler 2k +1, et un nombre pair on va l’appeler simplement 2k, c’est un multiple de 2, (V02-12.40) ; JMV20150602, |
||||||||||||||||||||||||||||||||||||||||||||
unilatère |
✔ |
- signifie que la surface n'a qu'une face (comme une bande de Moebius), elle est non-orientable. p61 - s'il existe dans un Nœud un vide de valence impaire, alors la surface du nœud est unilatère. Np66 - exemple : le noeud de Trèfle dont la surface d'empan est unilatère, monochrome, elle peut être réorientée par une coupure. 222-33 |
||||||||||||||||||||||||||||||||||||||||||||
urverdrangt |
✔ |
- l'Oeuvre de Mélanie Klein qui est dirigée et trébuchante, tout le monde dans la psychanalyse voudrait faire la peau à ce truc pré-oedipien, et Lacan nous dit c'est pas possible, c'est pas possible comme ça, c'est pas observable, on ne peut pas dater le trauma, on ne peut pas dater l'urverdrangt, on ne peut pas dater l'incorporation, JMV09092014, 22.39, | ||||||||||||||||||||||||||||||||||||||||||||
| V, | ✔ |
|||||||||||||||||||||||||||||||||||||||||||||
✔ |
- Vappereau.Jean-Michel, Professeur de Mathématique, logicien, topologue et psychanalyste français. XX et XXI eme Siècles. ( Achèvement de la psychanalyse, enseignement, gravitation/inertie du langage, Champ de lisibilité du noeud) . Achève et enseigne - en France, aux Amériques, au Levant - la psychanalyse de Freud et de Lacan. * Propose une théorie mathématique et une figuration nodale de l'appareil psychique et de l'inconscient en introduisant une nouvelle négation.. Pour les noeuds, il définit leur Champ de lisibilité...(coupures et incorporelles). Jean-Michel Vappereau expose la 3eme analyse connue, effective, après Freud et Lacan. Il invite chacun à se saisir d'une nouvelle écriture qui veut faire lien. - Site de JMV et textes, site TEE e-toplogie, (Topologie En Extention), - Enseignement en France, en Argentine, en Colombie, au Canada, en Espagne, ... - Chronologie de l'enseignement de J-M.Vappereau à Paris de 1993 à 2014, (out) - Textes, cours et conférences inédites... et ici et là aussi, et un ouvrage rare, épuisé : Essaim, version gaogoa - Programme de recherche du Professeur Vappereau formulé lors du Séminaire La Topologie et le temps, du Dr J.Lacan, le 15 juin 1979, http://gaogoa.free.fr/Seminaires_HTML/26-TT/L15051979.htm |
|||||||||||||||||||||||||||||||||||||||||||||
Variétés
|
✔ |
- pour le noeud, c'est l'espace autour du noeud, la variété du noeud, que l'on peut étudier au moyen des techniques de la topologie algébrique, voir de la géométrie différentielle. -L'objectif fut de généraliser les propriétés métriques et différentielles des surfaces "usuelles" de l'espace euclidien à des espaces "courbés" considérés comme espaces de référence et non plus comme plongés dans un espace plus vaste de dimension supérieure : on parle de variétés . Une variété est dite algébrique si elle admet une équation polynomiale du type f(x,y,z,...) = 0. Une conique , un cercle sont des variétés algébriques de dimension 1, la sphère est une variété algébrique de dimension 2 ( surface ). ....suite des définitions sur Chronomath - en géométrie, en géométrie algèbrique, en algèbre, - La topologie algébrique cherche à classer les variétés (mais aussi des objets plus généraux) en en déterminant des invariants , c'est-à-dire des objets mathématiques — qui peuvent être des nombres réels — associés à chaque variété et qui en caractérisent la topologie. Certaines variétés sont munies de structures plus fortes : il est du ressort de la topologie différentielle , puis de la géométrie différentielle , de la géométrie riemannienne et de la géométrie symplectique de les étudier et de les classifier. |
source Wiki , | |||||||||||||||||||||||||||||||||||||||||||
| - Variétés topologiques, On définit aujourd'hui abstraitement une variété topologique V de dimension n comme un espace topologique connexe séparé localement homéomorphe (homéomorphisme = bijection continue ainsi que sa réciproque) à un ouvert de Rn : chaque point de V admet un voisinage ouvert homéomorphe à un ouvert de Rn. On parle de variété topologique de dimension n. Lorsque n = 3, le très important et vaste sujet des variétés de dimension 2 est l'étude des surfaces, comme la sphère. |
||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
| 3. les variétés à bord : le bord (ou frontière) d'une variété fermée (au sens topologique) est l'ensemble de ses points frontières également dits points bordants. Comme dit ci-dessus, on les caractérise par le fait que tout voisinage d'un point frontière déborde dans l'espace environnant contrairement aux variétés closes où tout voisinage de tout point y est entièrement inclus. | ||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
| . Dans le plan R², le bord du disque fermé x²+y² ≤ 1 est le cercle unité, noté S1, de dimension 1. Dans R, le bord de l'intervalle fermé [-1,1] est la paire {-1,1} de dimension 0. | ||||||||||||||||||||||||||||||||||||||||||||||
Vel↑ Velle |
✔ |
- sur l'opéreur logique OU, symbole ∪, les 3 formes du OU ( inclusif, exclusif, aliénant), (et non 2 !) - Vel de l'aliénation,<≠, il est l'abréviation de l'expression formée par les seuls connecteurs primitifs de la négation et de la disjonction exclusive classique - pour Velle voir Séparation |
||||||||||||||||||||||||||||||||||||||||||||
Vérifonctionnalité↑ |
✔ |
- voir Théorie de la vérifonctionnalité, ci-dessus, - du Vrai et Faux, - La LCC, in L'amour du tout aujourd'hui, 2 eme partie, JMV, 1992 - Clef pour la passe, 1ere partie, argument 3, dans L'amour du tout, JMV - Clef pour la passe, 2 eme parie, dans L'amour du tout, JMV, entre intrinsèque et extrinsèque |
||||||||||||||||||||||||||||||||||||||||||||
Vérité ↑ |
✔ |
- La vérité parle, le savoir écrit ! - la parole c'est continue et que ça dit la vérité, alors que l'écriture est discrète et produit du savoir, c'est à cette occasion là qu'on parle du savoir, qui n'est pas la connaissance, ce n'est pas non plus un savoir faire, c'est un savoir lire, savoir écrire, savoir compter, le savoir ça commence avec la différence entre l'écrit et la parole, JMV09092014, - le prédicat de vérité, - V et F, en logique, , -Le vel de l'aliénation, 2006, JMV ; - L'amour du tout aujourd'hui, 1ere partie , la fonction phallique, Cs et Ics avec Wundt, Tarski, prédicat, induction déduction assimilation, métalangage - La LCC, in L'amour du tout aujourd'hui, 2 eme partie, JMV, 1992 - Clef pour la passe, 1ere partie, argument 3, dans L'amour du tou, JMV, écriture de la vérité - Clef pour la passe, 2 eme partie, Ecriture du mode moyen de la vérité, JMV - une définition subjective de la vérité, qui tient (enfin) compte de la place prépondérante du sujet dans l'énonciation. in GIRARD.J-Y, Le point aveugle, T2, Vers l'imperfection, - Si dire c'est dire la vérité, (fut-elle fausse !), Qu'on dise reste oublié derrière ce qui se dit dans ce qui s'entend ! in l'Etourdit, Autres Ecrits , LACAN, |
||||||||||||||||||||||||||||||||||||||||||||
| - voir Théorie de la vérifonctionnalité, | ||||||||||||||||||||||||||||||||||||||||||||||
| - que p, c’est l’écriture de l’affirmation, qui n’est pas l’assertion, parce que l’assertion c’est 1, c’est le problème de la vérité chez Tarski, on verra que justement la définition du prédicat de vérité, ce qui l’amène à introduire le fait qu’il ne faut surtout pas que ce soit des langages sémantiquement clos, ça va être le fait qu’il y a encore une analyse insuffisante de la différence qu’il y a entre la vérité apophantique empirique, la vérité d’une proposition, et puis l’énonciation, l’assertion, la vérité logique, celui qui le dit mieux, même beaucoup mieux que Wittgenstein c’est Frege, Frege dit ça comme ça, il dit : ça ne sert à rien de dire que quelque chose est vrai parce que ça n’ajoute aucune vérité à la chose. JMV20150609 | ||||||||||||||||||||||||||||||||||||||||||||||
Vide↑ |
✔ | - Le vide est défini par l'ensemble vide Ø |
||||||||||||||||||||||||||||||||||||||||||||
- En mathématiques, l'ensemble vide est l'ensemble ne contenant aucun élément. L'ensemble vide peut être noté d'un O barré1, à savoir Ø ou simplement { }, qui est une paire d'accolades ne contenant qu'une espace, pour représenter un ensemble qui ne contient rien. La notation Ø a été introduite par André Weil, dans le cadre de l'institution de notations par le groupe Bourbaki 2. Von Neumann dans son article de 19233,4, qui est l'une des premières références qui l'aborde, le note O. |
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
L'ensemble vide ne contient rien, mais comme c'est un ensemble, il n'est pas rien. C'est la base sur laquelle s'appuie von Neumann 3,4 pour construire les entiers et les ordinaux. La notation { Ø} n'a pas le même sens que la notation Ø ; en effet, l’ensemble désigné par Ø n'a aucun élément (car c’est l'ensemble vide), tandis que l’ensemble désigné par { Ø} en a un (cet élément est l'ensemble vide). D'ailleurs, von Neumann définit 0 comme étant Ø et 1 comme étant { Ø}. Rappelons (voir supra) que l'ensemble vide est un sous-ensemble de n'importe quel ensemble A, c'est-à-dire que pour tout élément x de Ø, x appartient à A, ce qui s'écrit formellement : (∀x ∈ Ø) x ∈ A. Plus généralement, un énoncé de la forme « tout élément de l'ensemble vide possède la propriété P », ou plus formellement (∀x ∈ Ø) P(x) (en), qui est une abréviation de ∀x (x ∈ Ø ⇒ P(x)), est toujours vrai, par ex falso quodlibet ; de même, tout énoncé de la forme «il existe un élément de l'ensemble vide possédant la propriété P » est toujours faux (ce second résultat est sans doute plus évident, mais ce n'est que la négation de l'affirmation précédente). L'axiome de fondation affirme que toute suite x0 ∋ x1 ∋x2 … se termine, donc il existe un n tel que, dans cette suite, xn = Ø. |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
L'ensemble vide est essentiel dans la théorie des ensembles ou théorie ZFC, son existence est assurée par l'axiome de l'ensemble vide. Son unicité découle de l'axiome d'extensionnalité. De plus, on peut démontrer en utilisant le schéma d'axiomes de compréhension, que l'existence d'un ensemble quelconque implique l'axiome de l'ensemble vide, ce qui évite, quand on formalise la théorie des ensembles en logique du premier ordre, de faire appel à un axiome spécifique pour l'existence de l'ensemble vide (voir axiome de l'ensemble vide). |
↑ | |||||||||||||||||||||||||||||||||||||||||||||
Point de vue catégorique : L'ensemble vide peut être caractérisé très simplement comme objet de la catégorie des ensembles. C'est en effet l'unique objet ayant la propriété suivante : Pour tout ensemble E, il existe une et une seule flèche de Ø vers E. Dans le cas de cette catégorie, flèche signifie application. Plus généralement, un objet qui, dans une catégorie, a cette propriété est appelé un objet initial. |
||||||||||||||||||||||||||||||||||||||||||||||
| - Vide physique :
En physique, le vide est l'absence de toute matière. Le vide absolu est donc un milieu statistiquement sans particules élémentaires. Un espace dans lequel les molécules sont fortement raréfiées peut donc être retenu comme une première définition du vide approximatif. Ainsi, il suffit d’utiliser une pompe à vide pour extraire l’air d'une enceinte étanche pour y « faire le vide ». La qualité du vide est alors définie par la pression d'air résiduelle, généralement exprimée en pascal, en millibar ou en torr. Seul un vide partiel peut être atteint avec un tel processus, quelle que soit la température. Le vide en astronomie se rencontre dans l'espace entre les corps célestes, ce que l'on nomme « espace ». Une pression de l'ordre de 10−8 Pa est appelée ultravide1, ce qui, aux températures usuelles (300 K), correspond à une densité de l'ordre d'une dizaine de millions de molécules par centimètre cube. Par comparaison, la densité au sein des gaz interstellaires est de l'ordre de 1 atome par centimètre cube |
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
| Vide quantique : En physique, le vide quantique décrit l'état du vide selon les principes de la mécanique quantique. Alors que l'on croyait l'univers rempli d'éther, la physique du XXe siècle a abandonné cette notion pour un espace littéralement vide de matière. Les principes quantiques montrent que ce vide est en réalité rempli d'énergie qui engendre de nombreux effets : on parle alors d'énergie du vide. |
W, |
↑ | ||||||||||||||||||||||||||||||||||||||||||||
Vie |
✔ |
- La vie pour Kant dans Premiers principes métaphysiques de la science et de la nature, c'est le pouvoir qu'a une substance de se déterminer à agir en vertu d'un principe interne. google-books : 6 sections, - Voir CANGUILHEM.Georges, W, La connaissance de la vie, 1993, Vrin, - Voir DESCARTES, ... - voir Vitalisme, W, |
||||||||||||||||||||||||||||||||||||||||||||
Le vitalisme s’oppose au « mécanisme », voire au « machinisme », qui réduisent les êtres vivants à des composés de matière, à l’instar d’une machine ou d’un robot. Le mécanisme est aujourd’hui la vision dominante dans les sciences physiques. En biologie, ce cadre théorique revient régulièrement dans l'histoire des sciences. Le terme désigne parfois la vision philosophique défendue autrefois par l'école de Montpellier |
||||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
| Le vitalisme est une doctrine dans laquelle on admet que les phénomènes vitaux de l'organisme (accroissement, développement du plan héréditaire, nutrition, etc.), loin de s'expliquer par le simple jeu des forces physico-chimiques, sont dus à l'action d'un principe vital conçu, soit sous forme d'une âme intelligente (vitalisme de Stahl), soit sous forme d'un archée subalterne (vitalisme de Van Helmont). Le vitalisme a aussi été professé sous une nouvelle forme par l'école de médecine de Montpellier, et son plus célèbre défenseur est Barthez. On peut alors le faire remonter, jusqu'à la doctrine du philosophe anglais Cudworth. | ||||||||||||||||||||||||||||||||||||||||||||||
Violence↑
|
✔ | - pacte social du rejet de la sexualité freudienne et de l'inconscient -Écrits p 810 |
||||||||||||||||||||||||||||||||||||||||||||
Vocabulaire de logiques |
✔ |
- Vocabulaire de logique ... en cours | ||||||||||||||||||||||||||||||||||||||||||||
| Vocabulaire de Mathématiques | ✔ |
- Vocabulaire de mathématiques, ici même | ||||||||||||||||||||||||||||||||||||||||||||
Voix↑ |
✔ |
- le voix c'est la lisibilité dans l'invocation, - la voix est associée à la Bouteille de Klein dans l'analyse - la voix manifeste le fait de dire, affirmation phallique, dans le territoire, d'ordre éthologique. Organe de la prestance du Maître. Les animaux parlent aussi, mais eux n'écrivent pas ! Leur territoire est sans porte. C'est le loft de notre époque de psychose généralisée! - La voix est la manifestation de la puslion invoquante. - La voix est du côté de l 'hypnose maternelle (par opposition à l'hypnose paternelle liée au regard (pendule) (montrer-voir), au scopique, Roger.Gentis). La b... a des yeux mais pas d'oreilles !. - la voix c'est un processus continue , et le propre de l'écriture c'est justement de découper, la lecture et l'écriture c'est de la découpe , et vous avez ça dès les premières pages de Freud, 0.32.44, et vous avez ça dès les premières pages de Freud sur les Aphasies (JMV09092014) - La voix comme "corporelle" ! . Les incorporel(le)s et la voix : La fonction (les mathématiques), l'application (la topologie) * , l'analyse ( la logique ), ces trois incorporels topologicomathématiques s'ajoutent aux Lekton, incorporels logico-sémantiques (le signifié ou l'exprimable ou dicible : Ce signifié qui est dévoilé dans le langage par la pensée est donc incorporel, alors que l'émission vocale et ce qui porte le nom sont corporels. Dans la mesure où le dicible est un état de chose pensé, il définit la sphère du vrai et faux : l'état de chose signifié et dicible est vrai ou faux.; ) et aux incorporels physiques : Vide, Temps, Lieu. Trois nouveaux inorporel(le)s, (Fonction, Aplication, Analyse), que Lacan cite dans Radiophonie , (Lacan, 1970, Autres écrits, Seuil, p408-409. Question II , ou Scilicet 2/3 p60 ) |
||||||||||||||||||||||||||||||||||||||||||||
| W, | ||||||||||||||||||||||||||||||||||||||||||||||
Whitehead (noeud de) |
✔ |
- sur le noeud de Whitehead, et, W1, W2, - 3322-433, - Une relation entre le Whitehead et les termes de la formule du fantasme, JMV.pdf |
||||||||||||||||||||||||||||||||||||||||||||
Whitehead (mouvement de ) |
✔ |
- le mouvement de Whitehead ou quart de tour, ou mouvement hybride Nh | ||||||||||||||||||||||||||||||||||||||||||||
Wundt
|
✔ |
- Wundt, Langage, sur gaogoa, - Wundt sur wiki - L'amour du tout aujourd'hui, 1ere partie , la fonction phallique, Cs et Ics avec Wundt, Tarski, - l’objection que fait Wundt à Freud, il lui dit on ne peut pas parler d’Inconscient parce que si l’inconscient c’est équivalent au non conscient, alors c’est du non psychisme, le psychisme inconscient équivalent à du non psychisme, le psychisme inconscient équivalent à du non conscient ça équivaut à du non psychisme, ce qui ne voit pas Wundt c’est qu’on peut ici changer les négations modifiées, les prendre dans un autre nœud, qui n’est pas le même nœud que celui dans lequel on est en train d’écrire toute la phrase, ce qui se fait en logique en général, Wundt il ne pouvait pas imaginer des choses comme ça, ça confirme que Freud a raison de maintenir que si on en a pas la pratique, qui est pour Freud une pratique de langue parlée, il analyse les rêves dans la langue parlée, JMV23062015, |
||||||||||||||||||||||||||||||||||||||||||||
| X, | ||||||||||||||||||||||||||||||||||||||||||||||
x, |
✔ |
- variables pour l'arithmétique et l'algèbre - inconnu(e), def Wiki - voir y , |
||||||||||||||||||||||||||||||||||||||||||||
| Y, | ||||||||||||||||||||||||||||||||||||||||||||||
y, |
✔ |
- y et x désignent les axes orthogonaux des coordonnées cartésiennes (wiki) - variables pour l'arithmétique et l'agèbre, -w, x, y, z, sont des lettres que l'on affecte en algèbre ou en géométrie aux variables inconnues... Alors que les lettres a, b, c, d ....sont elles des lettres réservées pour des valeurs constantes.... |
||||||||||||||||||||||||||||||||||||||||||||
| Z, | ||||||||||||||||||||||||||||||||||||||||||||||
Z2 |
✔ |
- Z2, 0, (zéro), c’est la classe de tous les nombres pairs et 1, (un) c’est la classe de tous les nombre impairs, grâce à cette notion de nombre pair et impair, si vous voulez regarder ça de plus près, vous verrez que vous pouvez additionner les nombre pairs et les nombres impairs de telle manière que la somme de deux nombres pairs ça donne un nombre pair, un nombre impair plus un nombre pair ça donne un nombre impair, et un nombre impair plus un nombre pair, ça donne un nombre impaire, et un nombre impair plus un nombre impair ça donne un nombre pair. - Voir Noeuds logiques, noeuds mathématiques, ci-dessus, |
||||||||||||||||||||||||||||||||||||||||||||
Zermelo-Fraenkel ZF S0T0
=
∈ |
✔ |
- c’est toujours une erreur d’expliquer la Logique par la Théorie des ensembles parce que c’est le contraire, c’est la Théorie des ensembles qui peut être écrite grâce à la Logique. - La théorie des ensembles de Zermelo-Fraenkel, ( ZF), (S0T0), ne connait que les ensembles. Son élégance conceptuelle et son aptitude à élaborer en son sein la quasi totalité des outils de la mathématique actuelle l'impose. -En mathématiques, la théorie des ensembles de Zermelo-Fraenkel, abrégée en ZF, est une axiomatisation en logique du premier ordre de la théorie des ensembles telle qu'elle avait été développée dans le dernier quart du XIXe siècle par Georg Cantor. L'axiomatisation a été élaborée au début du XXe siècle par plusieurs mathématiciens dont Ernst Zermelo et Abraham Fraenkel mais aussi Thoralf Skolem. Cette axiomatisation échappe aux paradoxes d'une théorie trop naïve des ensembles, comme le paradoxe de Russell, en écartant le schéma de compréhension non restreint (le fait que toute propriété puisse définir un ensemble, celui des objets ayant cette propriété) pour n'en conserver que certains cas particuliers utiles. De ce fait il existe des classes, des collections d’objets mathématiques définies par une propriété partagée par tous leurs membres, qui ne sont pas des ensembles. Dans la théorie ZF et ses extensions, ces classes dites classes propres ne correspondent pas à des objets de la théorie et ne peuvent être traitées qu'indirectement, à la différence de la très voisine théorie des classes de von Neumann-Bernays-Gödel (NBG). En raison de son statut particulier, on considère en général que l'axiome du choix ne fait pas partie de la définition de ZF et on note ZFC la théorie obtenue en ajoutant celui-ci. [ abrégé en « AC », est un axiome de la théorie des ensembles qui « affirme la possibilité de construire des ensembles en répétant une infinité de fois une action de choix, même non spécifiée explicitement".W] Les mathématiques usuelles peuvent être théoriquement développées entièrement dans le cadre de la théorie ZFC, éventuellement en ajoutant des axiomes, comme les axiomes de grands cardinaux, pour certains développements (ceux de la théorie des catégories par exemple). En ce sens il s'agit d'une théorie des fondements des mathématiques. En 1963 Paul Cohen utilise la théorie ZFC pour répondre à la question posée par Cantor de l'hypothèse du continu, en montrant qu'elle n'était pas conséquence des axiomes de cette théorie, et que l'axiome du choix n'était pas conséquence de la théorie ZF. La méthode qu'il développe, le forcing, est à l'origine de nombreux développements de la théorie des ensembles. La très grande majorité des travaux des théoriciens des ensembles depuis au moins cette époque se situent dans le cadre de la théorie ZF, de ses extensions, ou parfois de ses restrictions. La constructibilité, une méthode développée par Kurt Gödel en 1936 dans le cadre de la théorie NBG pour montrer que l'hypothèse du continu et l'axiome du choix n'étaient pas en contradiction avec les autres axiomes de la théorie des ensembles, s'adapte immédiatement à la théorie ZF. |
||||||||||||||||||||||||||||||||||||||||||||
Zéro |
✔ |
- de l'arabe sifr par l'italien, "vide" , - voir Z2 ci-dessus, |
||||||||||||||||||||||||||||||||||||||||||||
| ↑ | ||||||||||||||||||||||||||||||||||||||||||||||
ZFC |
✔ | - En mathématiques, l'abréviation ZF désigne la théorie de Zermelo-Fraenkel, - En raison de son statut particulier, on considère en général que l'axiome du choix ne fait pas partie de la définition de ZF et on note ZFC la théorie obtenue en ajoutant celui-ci. [ abrégé en « AC », est un axiome de la théorie des ensembles qui « affirme la possibilité de construire des ensembles en répétant une infinité de fois une action de choix, même non spécifiée explicitement".W] -Les mathématiques usuelles peuvent être théoriquement développées entièrement dans le cadre de la théorie ZFC, éventuellement en ajoutant des axiomes, comme les axiomes de grands cardinaux, pour certains développements (ceux de la théorie des catégories par exemple). En ce sens il s'agit d'une théorie des fondements des mathématiques. En 1963 Paul Cohen utilise la théorie ZFC pour répondre à la question posée par Cantor de l'hypothèse du continu, en montrant qu'elle n'était pas conséquence des axiomes de cette théorie, et que l'axiome du choix n'était pas conséquence de la théorie ZF. La méthode qu'il développe, le forcing, est à l'origine de nombreux développements de la théorie des ensembles. La constructibilité, une méthode développée par Kurt Gödel en 1936 dans le cadre de la théorie NBG pour montrer que l'hypothèse du continu et l'axiome du choix n'étaient pas en contradiction avec les autres axiomes de la théorie des ensembles, s'adapte immédiatement à la théorie ZF. |
- W,
|
↑ | ||||||||||||||||||||||||||||||||||||||||||
Zorro |
✔ |
- Les séminaires de Lacan source Zorro | ||||||||||||||||||||||||||||||||||||||||||||