Nombres *, seul langage universel ? et noeuds                en cours de composition
Dans l'Ancien testament "les Nombres" constituent un chapitre dont l'objet est le recensement exhausif des filiations, des généalogies, des tribues d'Israël !

ambition et but !

Les nombres entiers naturels : un entier naturel est un nombre positif ou nul permettant fondamentalement de dénombrer des objets comptant chacun pour un . Un tel nombre entier peut s'écrire avec une suite finie de chiffres en notation décimale positionnelle , sans signe et sans partie fractionnaire , c'est-à-dire sans chiffre « après la virgule ». Les entiers naturels sont donc, outre zéro , ceux que l'on commence à énumérer avec la comptine numérique : un , deux , trois , quatre … Mais la liste des entiers naturels est infinie , car chacun d'entre eux a un successeur , c'est-à-dire un entier qui lui est immédiatement supérieur. wiki.
Théorème fondamental de l'arithmétique : Théorème fondamental de l'arithmétique  —  Chaque entier strictement positif peut être écrit comme un produit de nombres premiers d'une unique façon, à l'ordre près des facteurs .
..de l'Un (Hénologie) :
Cardinaux, ordinaux. Continu (discret), dicontinu , fini, infini,
Les bases (2,..10, 12, 20, 60, ....)
Le zero et le sexuel : séries convergentes, séries divergentes, hystérique *: symptôme dernier !, ....congruence : les suites passent par Zéro ! (Zéro sexuel ou zéro générateur, de génération)

suite infinie des nombres entiers	1	2	3	4	5	6	7	8	9	10	11	..	tables a, b,
		entier et premier

Ils organisent des cycles reproductifs pour des espèces de cigales...., des répétitions cycliques pour les marées, les astres...,

Hypothèse de Riemann : Le chaos des nombres premiers cache un schéma ordonné, une harmonie interne
Le plus grand nombre premier connu : Les nombres premiers sont en quantité infinie.( Euclide, Proposition 20, Les Eléménts). En 2009, le plus grand nombre premier connu est , qui comporte 12 978 189 chiffres en écriture décimale. (source wiki). Il ne faudrait pas moins de 2 semaines pour le lire à haute voix ! Ce nombre est bien supérieur aux 100 nombres composant le chiffre des atomes contenus dans l'Univers ! La liste à jour !
Les nombres parfaits : entier égal à la somme de ses diviseurs : 6 = 1 + 2 +3
Les nombres premiers jumaux : La conjecture des nombres premiers jumeaux se demande s'il y a un nombre infini de nombre premiers p tel que p + 2 est également un nombre premier.
La paire 71 et 73 ou 1 000 037 et 1 000 039 en sont des exemples.
Les nombres amicaux : 220 et 284; 1184 et 1210;..; où la somme des diviseurs de l'un coincide avec la somme des diviseurs de l'autre, et si les deux sommes valent la somme des deux nombres.
Les nombres triangulaires : 1, 3, 6, 10, 15 : où un nombre est le composé de son précédant additionné au rang qu'il occupe (ici 3 est au rang 2, 6 est au rang 3, 10 est au rang 4..)
, ou n indique le rang, formule connue depuis Pythagore (emrpunt de la formule à wikipedia)
La méthode du crible d'Eratosthène : Villemin, Eveilleau, Wiki,
Nombre de Fermat : soit un entier n; claculer m = 2 puissance n; calculer 2 puissance m + 1; (2,4,17)
Petit théorème de Fermat (Diophante (ensemble des rationnels positifs), Fermat (domaine des nombres entiers), Wallis, Fenicle ) : "Pour tout nombre premier p , et tout nombre a non divisible par p, on a a (puissance p-1) =(équivaut à ) 1 ( modulo p)" p112 Une histoire des mathématiques, Dahan-Dalmedico, point Seuil S49 (Euler, Lagrange..) : (source wiki)
Dernier théorème de Fermat : Il n'existe pas de nombres entiers non nuls , x, y, et z tels que : dès que n est un entier strictement supérieur à 2, ou
Hypothèse de Fermat :
"Pour n entier plus grand que 2, l'égalité x (puissance n) + y (puissance n) = z (puissance n) est impossible dans l'ensemble Z et dans l'ensemble Q" * . (3,4,5 et 5,12,13 ) .
Arithmétique de l'horloge de Gauss ou arithmétique modulaire p23, 39: Gauss,
(voir horloge in Fibonnacci, ), arithmétique modulaire : wiki, 2,
Suite, Série, Chaîne,..: Suites (wiki, les suites ). Séries (wiki, discussion, cours). Chaîne numérale( wiki,
La suite de Fibonnacci : De nombreux organismes, systèmes, sont régis par la notion de cycles (reproduction des lapins, pétales des fleurs, spirale des pommes de pin, ...), F suite,
Le nombre d'or : 1,61803, wiki, le nombre d'or,
Pi : 3,141592..., Π, Π et Ramanujan, l'univers de Π,
Conjoncture de Goldbarch : stipule que tout nombre entier pair strictement supérieur à 3 peut être écrit comme la somme de deux nombres premiers (le même nombre premier pouvant être utilisé deux fois). ou autre formule : Tout nombre entier strictement supérieur à 1 est la moyenne arithmétique de deux nombres premiers . 10=3+7=5+5
La conjecture a été vérifiée par ordinateur pour tous les nombres pairs jusqu'à 2.10 (puissance 18) à la date de novembre 2010 !
Fonction trigonométrique : les fonctions trigonométriques sont des fonctions dont la variable est un angle . Elles permettent de relier les longueurs des côtés d'un triangle (t???????, trigonon en grec) en fonction de la mesure des angles aux sommets. les fonctions trigonométriques sont importantes pour étudier les triangles, les cercles (on les appelle aussi fonctions circulaires ) et modéliser des phénomènes périodiques .
Série trigonométrique : Une série trigonométrique est une suite particulière de polynômes trigonométriques . La série possède une fréquence fondamentale f , et on somme successivement des fonctions trigonométriques de fréquence n.f pour des valeurs entières de n .
Les nombres de Mersenne : En mathématiques et plus précisément en arithmétique modulaire , un nombre premier de Mersenne est un nombre premier s'écrivant sous la forme 2 p - 1, p étant premier.
Les nombres premiers de Mersenne sont liés aux nombres parfaits , qui sont les nombres égaux à la somme de leurs diviseurs propres. C'est cette connexion qui a motivé historiquement l'étude des nombres premiers de Mersenne.
Les nombres rationnels ( conforme à la raison) ou de ration (portion, part..) : fraction et écriture décimale
Les nombres négatifs :
Règle des parties :
Théorie des jeux :
Triangle de Pascal :
Le pari de Pascal :
Les carrés magiques : disposition de nombres entiers, en autant de lignes que de colonnes, en sorte que la somme des nombres écrits sur chaque ligne, sur chaque colonne, sur chaque diagonale soient toutes égales. (816-357-492) (1 carré magique avec les 9 premiers entiers, 880 avec les 16 premiers, plus de 300 millions avec les 25 premiers entiers !)
Table d'Euler :
Logarithme : (Gauss, Mersenne, Legrand ). Wiki, Villemin.
Le logarithme de base b d'un nombre réel positif est la puissance à laquelle il faut élever la base b pour obtenir ce nombre. Par exemple, le logarithme de mille en base dix est 3, car 1000 = 10 3 . Le logarithme de x en base b est noté log b ( x ). Ainsi log 10 (1000) = 3.
e = 2,7182 Gauss
La fonction de Legendre (logaritme et nombres premiers) :
Conjecture des nombres premiers de Gauss :
Nombre Imaginaire - i - : clé du monde subatomique,
Nombres irrationnels :
Nombres négatifs :
La fonction : Cauchy
Fonction sinus :
L'horloge de Gauss : arithmétique modulaire,
Fonction logarithmique de Gauss :
Pytagore, la musique des sphères : Harmonie décelée par Pythagore dans la suite des nombres 1, 1/2, 1/3, 1/4, ... correspondant au remplissage d'urnes d'eau selon ces proportions créant une harmonie étendue à l'univers et nommée "musique des sphères". "La physique de la musique plonge ses racines dans les bases des mathématiques".(p124, du Sautoy, la symphonie des nombres premiers)
Séries harmoniques : la série harmonique est une série de nombres réels . C'est la série des inverses des entiers naturels non nuls.Elle fait partie de la famille plus large des séries de Riemann , qui sont utilisées comme séries de référence : la nature d'une série est souvent déterminée en la comparant à une série de Riemann et en utilisant les théorèmes de comparaison . série définie par             
On note classiquement H n la n-ième somme partielle de la série harmonique, qui est donc égal à :

Fonction Zeta et produit d'Euler : Formule ou théorème d'Euler :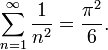
La fonction Zeta ? : En mathématiques , la fonction de Riemann est une fonction analytique complexe qui est apparue essentiellement dans la théorie des nombres premiers . La position de ses zéros complexes est liée à la répartition des nombres premiers.
Elle est aussi importante comme fonction modèle dans la théorie des séries de Dirichl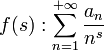et     
et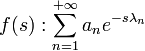
et se trouve au carrefour d'un grand nombre d'autres théories.
La dimension 4 : ex : le temps en physique. La 4 eme dimension permet de décrire un domaine en 4 dimensions (économique ?); pour la fonction zéta : 2 dimensions pour les coordonnées des nombres imaginaires, et 2 dimensions pour les deux coordonnées décrivant le nombre imaginaire produit par la fonction .
Ombres : Notre ombre est une image en D2 de notre corps en D3. A partir de l'ombre, silhouette, nous avons assez d'informations pour reconnaitre ce corps (sous un certain angle !) ! A l'aide de la fonction zeta nous pouvons construire une ombre tridimensionnelle du paysage édifié par Riemann en 4D à l'aide de la fonction zéta, et où l'axe nord-sud est la direction des nombres imaginaires, et l'axe est-ouest représente les nombres réels.
Il y a une perte d'information tout comme l'ombre perd des caractéristiques de l'objet ! il y a plusieurs ombres, plus ou moins informées !
Paysage de Riemann: Il recouvre toute la carte des nombres imaginaires. Paysage rigide ou certain lieu contiennent des informations sur l'ensemble du décor ! Et notemment les points situés "au niveau de la mer", dans ce monde imaginaire, disent tout, là où la fonction donne zéro ! Les zéros de la fonction zéta !


L'algèbre :
Les équations :
Degré des équations :
Les inéquations :
La proportionnalité :
Combinatoire et statistique :
Graphe et graphiques :
Hasard et probabilité :
L'analyse : Leibnitz ,

Desargues :
Dérivées :
Croissance, exponentiel, logarithme,
Les constantes : Pythagore, Archimède, Nombre d'or, Transcendant (Ch.Hermite), de Liouville, d'Euler, de Brun, d'Apéry,
Ensembles :