6




Pentachore *
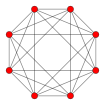
Tesseract *
Hexadécachore *
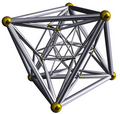
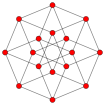
Icositétrachore *
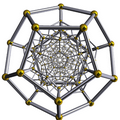
Hécatonicosachore *
Hexacosichore *

















| Ouverture Polygones Polyèdres Platon Kepler-Poinsot Archimède Catalan Johnson Trapèzes Pyramides Diamants Polychores Schafly Polytopes Révolution | ||||||
| vers D3 | convexes | 6 |
POLYCHORES | |||
| D4 |  |
 |
 |
 |
 |
 |
Pentachore * |
Tesseract * |
Hexadécachore * |
Icositétrachore * |
Hécatonicosachore * |
Hexacosichore * |
|
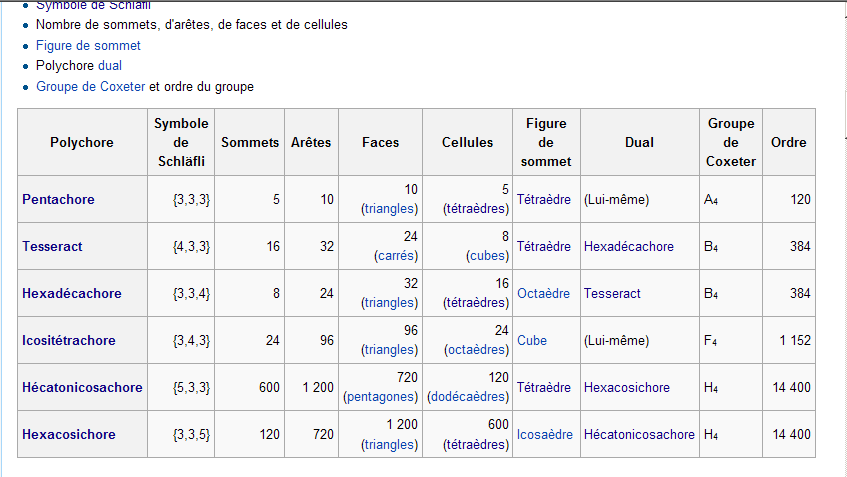
| Polychores | ||||||
| Type de face | triangles | |||||
| Configuration (figure) de sommets | Tétraèdre | Tétraèdre | Octaèdre | Cube | Tétraèdre | Icosaèdre |
| faces / | 10 ( triangles ) | 24 (carrés) | 32 (triangles) | 96 (triangles) | 720 (pentagones) | 1200 (triangles) |
| arrêtes | 10 | 32 | 24 | 96 | 1200 | 720 |
| sommets | 5 | 16 | 8 | 24 | 600 | 120 |
| caractéritique E-P : χ =S-A+F (khi) | ||||||
| Symbole de Shläfli | {3,3,3} | |||||
| Symbole de Wythoff | ||||||
| Diagramme de Coxeter-Dynkin | ||||||
| Groupe de Coxeter | A4 | B4 | B4 | F4 | H4 | H4 |
| Ordre | 120 | 384 | 384 | 1152 | 14400 | 14400 |
| Références d'indexation (à indicier) | ||||||
| Dual | lui-même | Hexadécachore | Tesseract | (Lui-même) | Hexacosichore | Hécatonicosichore |
| Groupe de symétrie | ||||||
| graphe | ||||||
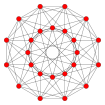
| Polygone de Pétrie |  |
 |
 |
 |
 |
 |
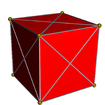
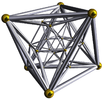
| Projection orthographique solide |  |
 |
 |
 |
 |
 |
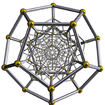
| Diagramme de Schlegel |  |
 |
 |
 |
 |
 |
| Projection stéréographique |  |
 |
 |
 |
 |
 |
 |
||||||
 |
||||||