4 solides de




Ne ratez pas
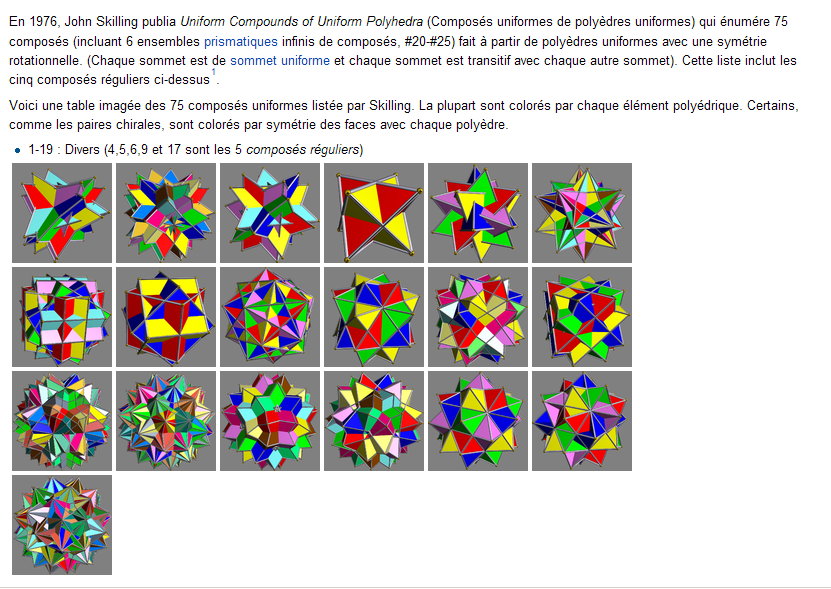
les 75 pollyèdres composés
de SKILLING ↓
C'est bijou !
les 75 pollyèdres composés
de SKILLING ↓
C'est bijou !
{5/2}
{5/2}
{5}
{3}
{5}
{3}
{5/2}
{5/2}
| Ouverture Polygones Polyèdres Platon Kepler-Poinsot Archimède Catalan Johnson Trapèzes Pyramides Diamants Polychores Schafly Polytopes Révolution | |||||
| vers D3 | concaves | 4 solides de |
Kepler-Poinsot | vers D3 | |
| D3 |  |
 |
 |
 |
Ne ratez pas les 75 pollyèdres composés de SKILLING ↓ C'est bijou ! |
| Invariants | Petit dodécaèdre étoilé | Grand dodécaèdre étoilé | Grand dodécaèdre | Gand icosaèdre | |
| Type | solides de Kepler-Poinsot | solides de Kepler-Poinsot | solides de Kepler-Poinsot | solides de Kepler-Poinsot | |
| Type de face | |||||
| Configuration de sommets | |||||
| faces | 12 {5/2} |
12 {5/2} |
12 {5} |
20 {3} |
|
| arêtes | 30 | 30 | 30 | 30 | |
| sommets | 12 {5} |
20 {3} |
12 {5/2} |
12 {5/2} |
|
| caractéritique E-P : χ =S-A+F (khi) | -6 | 2 | -6 | 2 | |
| Symbole de Schläfli | {5/2,5} | {5/2,3} | {5,5/2} | {3,5/2} | |
| Symbole de Wythoff | |||||
| Diagramme de Coxeter-Dynkin | |||||
| Type de face | |||||
| Références d'indexation (à indicier) | |||||
| Dual | Grand dodécaèdre | Grand isocaèdre | Petit dodécaèdre étoilé | Grand dodécaèdre étoilé | |
| Groupe de Symétrie | Ih | Ih | Ih | Ih | |
| Propriétés | |||||
| graphe | |||||