XXVI-La
topologie et le temps –1978-1979
12
décembre 1978
Je
me suis aventuré à annoncer que peut-être je prendrai un exemple de ce
qu’on appelle le « borroméen généralisé », c’est à savoir
que j’énoncerai comment on peut rendre borroméen, je veux dire à partir de
quel moment s’avère borroméen un nombre de cinq cercles, puisque dans le
borroméen c’est de cercle qu’il s’agit. Le borroméen généralisé, je
l’avais annoncé pour deux cercles retirés sur cinq. La solution m’a été
donnée en main par deux personnes, à savoir Madame Parizot dont j’espère
qu’elle est ici présente et un nommé Vappereau qui a bien voulu aussi
contribuer à cette solution.
Il
n’y a rien de plus facile que de rendre borroméen, c’est-à-dire de déchaîner,
c’est-à-dire de libérer cinq cercles. En voici un, en voici deux, voici le
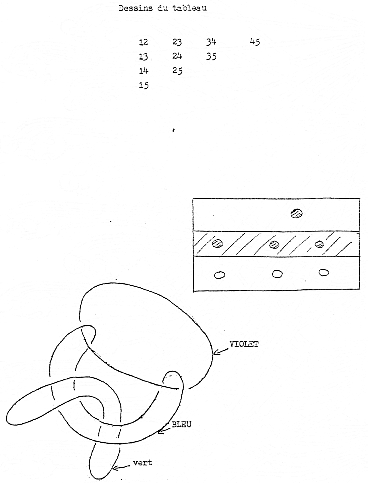
troisième, voici le quatrième et voici le cinquième. Ca c’est le troisième ;
ça c’est le deuxième. Le deuxième est violet, le troisième est en beige,
le quatrième est en vert et le cinquième est en rouge. La façon de libérer
deux cercles sur ces cinq est tout à fait clair. Les personnes qui s’en sont
mêlées ont bien voulu l’une et l’autre dire de quelle façon c’est
possible : c’est possible de dix façons. Il suffit de libérer, c’est-à-dire
de couper le 1 et le 2, le 1 et le 3, le 1 et le 4, le 1 et le 5, les trois
autres se déchaînent, comme il est facile de le voir du fait que ce violet-là
par exemple file jusqu’à se réduire à quelque chose qui vient là. Ce
violet se réduit à ce quelque chose qui glisse jusque là et qui, du fait du 5
disparu, est dénoué du vert, du beige et du violet. Ceci est libre, ces trois,
puisqu’il s’agit ici de cercles, ces trois cercles sont libres l-un par
rapport à l’autre. Le vert, le violet et le beige sont libres par rapport au
violet, à savoir que le vert se dénoue, le beige se dénoue aussi et le violet
ici se dénoue également.
Il
est facile de voir qu’en dénouant le 2 associé
au 3, le 2 associé au 4, le 2 associé au 5, on aura le même résultats.
Le 3 associé au 4 et le 3 associé au 5 aura le même résultat, le 4 associé
au 5 aura aussi le même résultat. Il y a donc dix façons de sectionner un de
ces cercles qui sont cinq, de les sectionner de façon à ce que le résultat
soit atteint.

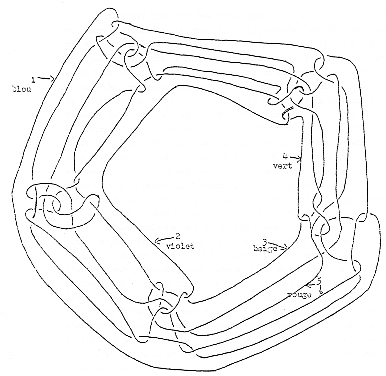
(p2->) J’ai poussé plus loin mon investigation, à savoir que j’ai interrogé sur un groupe de six cercles, j’ai questionné sur la façon dont on obtient un borroméen généralisé en en coupant trois. Il y a effectivement 35 façons de le faire. Pour cela, il faudrait, de la même façon que nous avons fait ces cinq cercles, en produire un sixième. Cette façon, je vous en dispense, car aussi bien çà serait un peu forcé. Mais il est possible de le construire. Parmi les 35 façons de couper les trois cercles en obtenant ce nœud que j’appelle borroméen parce qu’il est symbolisé à partir de trois, c’est-à-dire que les trois sont dénoués quand on retire un…il suffit d’en couper un pour que les trois autres soient dénoués.
Dans le borroméen à six, il suffit également d’en couper un pour que les six soient dénoués. Je précise qu’il y a dix façons de dénouer cinq cercles et qu’il y a trente cinq façons de dénouer six cercles en en coupant trois.
Peut-être je vais distribuer ce qui a été obtenu ce matin par Soury qui a bien voulu s’en charger de photocopie d’une photo en couleur, c’est-à-dire que les couleurs, elles, n’apparaissent pas, mais que, à couper trois de ces cercles, on peut s’apercevoir que les autres sont libres.
Ca demande un certain soin de colorier chacun de ces cercles. Mais on peut voir que çà marche. Ceci suppose qu’on en retire d’abord 2 et ensuite un troisième. C’est au troisième que chacun de ces cercles s’avère être libre. C’est vous Vappereau ? Je vous écoute.
VAPPEREAU : Vous faites une erreur dans la façon de compter les différentes manières de dénouer la chaîne à six en coupant trois. Vous avez donné le résultat pour la chaîne à sept en en coupant quatre, c’est à dire 35..
LACAN : J’ai dit qu’en en coupant trois sur les six, on obtient une chaîne borroméenne…
VAPPEREAU : Vous dites qu’il y a 35 façons de le faire, or il n’y en a que 20…
LACAN : Oui, c’est vrai qu’il n’y en a que 20. C’est vrai qu’il n’y en a que 20 et que, de ce fait, je me suis trompé. Eh bien, il me reste à m’en excuser et à vous promettre que, la prochaine fois, je ne vous entretiendrai pas sur les cercles.
Bien, au revoir !